内支线集装箱船最佳航态研究
姜伟 秦江涛 冯上民 裴志勇 吴卫国

摘 要:为有效提升船舶能效,本文针对内支线敞口集装箱船,通过数值计算分析,建立各典型载况及航速下船舶阻力与纵倾角度间的数学模型,从而在营运中通过航态最优化来实现船舶节能。
关键词:内支线集装箱船;最佳航态;船舶能效
中图分类号:U674.13+1? ? ? ? ? ? 文献标识码:A? ? ? ? ? ? 文章编号:1006—7973(2019)01-0030-03
1 研究背景
现如今,船舶工业进入到日益大型化和多样化的时代,造船业界都在通过各种办法来提升船舶的能效,各种新技术的应用已经成为国际海事界的共识。船舶能效的提升可有多种手段:如节能船型优化、节能附体开发、船舶动力废热回收与利用、电力系统优化管理、船舶航运管理方面的航线优化等,也即船舶能效贯穿于船舶的设计、制造和营运的整个生命周期。对于已投入营运的船舶,设计与建造阶段的节能措施不再适用,能效提升技术主要包括航行操纵管理(如合理配载以实现最佳航态)与船体和螺旋桨工况管理(如船体污底管理)。其中最佳航态是营运船舶能效提升的最有效手段,以最佳航态营运,可有效节能减排。
关于船舶航态对阻力、快速性以及能耗的影响研究很早就开始了,上海船舶运输科学研究所对散货船的纵倾试验表明最佳航态可节油4.0%-7.3%;大连理工大学对大型远洋货船的模型试验与实船自航结果表明最佳纵倾可实现日节油1.117t;中国船舶科学研究中心对七万吨级散货轮在不同吃水状态不同纵倾的27种方案系列试验表明最佳纵倾对船舶阻力的影响最大可达17%。近年来,针对最佳纵倾的研究逐渐从成本高昂的模型试验向低成本、高效率的数值模拟过渡,大连海事大学对灵便型游轮阻力的数值计算表明,最佳纵倾可降低静水阻力1.9%左右,排放指数可降低0.8%;华中科技大学对46000 t成品油轮的数值计算表明纵倾优化可降低船舶阻力4%-5%;武汉理工大学对开发的宽扁肥大型江海直达船阻力计算表明,最佳纵倾可减阻6.5%。
一般来说,通过纵倾调整实现船舶能耗降低既可适用于中低速运输船舶,也适用于较高航速的半滑行、滑行状态的船舶。而且纵倾调整在诸多船舶节能措施中不影响船舶的正常营运,仅通过合理配载或压载来调整船舶浮态,从而使船舶在特定排水量下以最佳航态来航行,因此是一个低风险、低成本的高效节能措施。在本文研究中,对一航行于南京龙潭港至上海洋山港间的256TEU集装箱船进行了系列载况不同航速下的阻力计算分析,得到一系列不同纵倾角对应的船舶阻力曲线,可得到船舶阻力最小时的最佳纵倾,装载时尽量使船舶浮态接近最佳纵倾角度,或通过压载水调整至最佳纵倾角,这样船舶在航行时阻力较小,燃油消耗较低,可实现节能减排。
2 最佳航态计算分析
2.1研究对象
研究对象为一航行于南京龙潭港至上海洋山港间的256TEU敞口集装箱船。该船主尺度如表1所示。本船为双底、双舷、单甲板结构,双机双桨推进的尾机型敞口集装箱船,具有球首双尾鳍船型。主船体由7道水密舱壁划分为首尖舱(兼压载水舱)、首泵舱、第一货舱(顶边舱设压载水舱、平台下为淡水舱)、第二货舱(顶边舱设压载水舱)、第三货舱(顶边舱设压载水舱)、机舱、淡水舱、舵机舱等。
2.2阻力数值预报方法
对于特定船型,其船舶阻力与载况(吃水和纵倾角)和航速息息相关,在给定载况与航速条件下的船舶阻力可采用基于求解RANS方程的數值方法进行预报,数值求解中考虑了船体随航速的纵倾与升沉变化。
2.2.1数值计算方法
2.2.1.1控制方程
船体绕流场中的流体为不可压缩粘性流,符合质量守恒定律与动量守恒定律,分别满足流体的连续性方程和纳维尔-斯托克斯方程(Navier-Stokes方程,简称NS方程)。
由于湍流在空间域时间域中的高频脉动,工程中难以通过直接求解NS方程的方法进行流场模拟,而往往采用求解时均化后的NS方程,即将NS方程取雷诺时均(RANS方程)是湍流场求解中通常采用的方法。由于RANS方程中出现额外的雷诺应力项,导致方程组数量少于未知物理量个数从而方程组不封闭,因此RANS方程的求解需增加额外的输运方程或雷诺应力张量,也即湍流模型。目前常见基于RANS方程的湍流模型主要包括涡粘模型和雷诺应力模型。
2.2.1.2湍流模型
如前所述,为使方程组封闭,需要对雷诺应力项建立对应的应力应变关系来封闭方程组。Boussinesq提出了重要的涡粘假定,其认为雷诺应力与平均速度梯度满足如下方程:
假定引入了湍动粘度项,因此雷诺应力求解的关键转到湍流粘度的确定上来。目前的工程应用中综合考虑计算效率与精度,通常采用两方程湍流模型,如k-ε模型及k-ω模型。本文采用建立在湍流充分发展基础上的标准k-ε模型。
2.2.1.3近壁处理方法
由于粘性与壁面影响导致出现边界层,其中流动参数沿壁面法向梯度较大需要高密度网格以捕捉流场特征,因此为降低网格需求工程应用中通常在近壁面流场区域采用壁面函数方法建立壁面上物理量与湍流核心区的流场参数建立联系。
2.2.1.4自由面处理
自由液面是船体绕流场中空气与水的交界面。因船体运动时自由面形状和位置发生改变,因此自由面求解是流场求解的一部分。自由面的处理方法主要包括界面跟踪法和界面捕捉法,本文采用流体体积法来捕捉自由面形状。
2.2.1.5航态求解方法
由于船体水动力分布的变化,有航速船舶的航态通常与静浮时的情形不同,因而航态是流场求解的一部分。本文根据船舶垂向受力与重力平衡来求解其升沉状况,根据船舶纵向力矩与纵倾回复力矩平衡来求解其纵倾状况,从而实现船舶航态的求解。
2.2.2 数值计算模型
2.2.2.1坐标系
采用右手惯性坐标系统,原点定义在静吃水面、纵中剖面与船中剖面的交点,x轴指向船尾为正,y轴指向右舷为正,z轴竖直向上为正。
2.2.2.2计算域与边界条件
由于采用随船坐标系,认为水流由前方匀速流向船舶,同时假定船舶绕流场对称,数值模型以半个船体及周围流体域为对象。计算域的船体边界采用无滑移壁面边界条件;计算域采用长方体形状,船前边界距船体1倍船长,侧面边界距船体1.5倍船长,顶面距甲板0.5倍船长,底面距静水面约2倍船长,均采用速度入口边界条件;船后边界距船体3倍船长,采用压力出口边界条件;计算域中纵中剖面所在平面为对称面。船体模型如图1,边界条件如图2所示。
2.2.2.3离散网格
计算域采用切割体网格形式进行计算域的离散,船体附近则采用棱柱层网格形式以保证壁面函数与流场捕捉对近壁面网格尺度的要求;同时为保证流场捕捉对船体、自由面附近网格密度的要求,在船体与无扰动的静水面附近采用若干网格密度盒(六面体形状)进行网格加密。部分剖面与无扰动静水面的网格分布如图3所示。
2.3 数值计算结果及分析
针对不同航速与重心纵向位置(与纵倾角对应)的内支线集装箱船进行了船舶绕流场数值模拟,并预报其船舶阻力。航速范围为7-13节(相应傅氏数变化从0.119到0.220),船舶重心纵向位置以正浮浮心为基准分别取-3%L,-2%L,-1%L,0%L,1%L与2%L(L为船长)等6种情况。
通过对不同航态与航速工况下的内支线集装箱船绕流数值模拟,可预报船舶阻力以及船体表面压力、自由面波形等流场细节。
2.3.1 船舶阻力
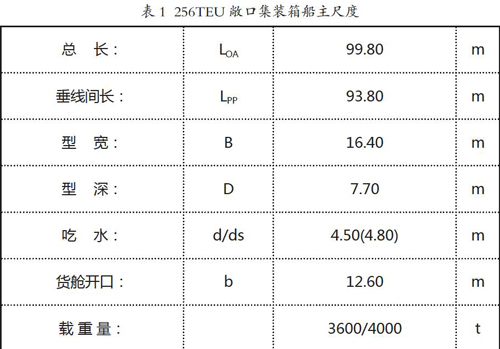
不同工况的船舶阻力数值计算结果如表2所示,船舶阻力关于航速与纵倾角(尾倾为正)的变化规律见图4所示。
由不同航速不同纵倾角的船舶总阻力系数曲线可见,对于某一营运航速,随着船舶浮态由首倾向尾倾变化,其阻力一般都是先降低再上升,在某一合适的纵倾角时船舶的阻力会最低;随着航速的提高,最小阻力所对应的纵倾角逐渐增大。在内支线船舶营运过程中,可利用上述计算结果使得船舶保持在最佳纵倾状态,从而有效实现节油。
2.3.2流场细节
某典型工况船舶绕流场的数值计算得到的船体表面压力(系数)分布云图如图5所示,其中压力系数定义为:
式中,p为压力,P0为大气压力,z為水深—即云图中的压力系数Cpd为去掉了重力与大气压强影响的水动压力(仅显示水线以下船体部分)。由压力分布云图可见,首倾时相当于船舶前体变的更为肥大,因此首部进流段缩短导致横向流动与舭涡较为严重,导致较低的首部压力以及严重的埋艏现象,从而使得船舶阻力增加。
数值模拟得到的兴波波形如图6所示,其中的波高以船长为特征尺度进行了无量纲化。由兴波波形图可见,首倾增大了前体的排水体积导致兴波现象更为明显,首波峰与前肩位置的波谷幅值与正浮与尾倾工况相比明显增大。
2.3.3计算结果分析与最佳纵倾
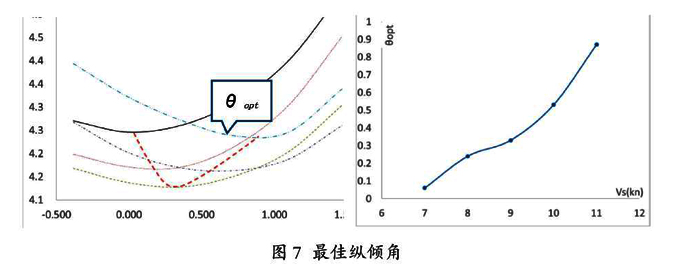
根据内支线集装箱船阻力随航速与纵倾角变化的计算结果可见,在给定航速下(营运航速)船舶阻力随总倾角变化较大,存在着最佳纵倾角度θopt,此时船舶的阻力最小。该船不同航速的最佳纵倾角总结于图7。
3 结论
“坚持把建设资源节约型、环境友好型社会作为加快转变经济发展方式的重要着力点”是国家规划纲要明确提出的目标,本文针对内支线敞口集装箱船,通过数值计算分析,建立各典型载况及航速下船舶阻力与纵倾角度间的数学模型,从而在营运中通过航态最优化来实现船舶节能,有效提升船舶能效。
该技术方案在航行于南京龙潭港至上海洋山港间的256TEU敞口集装箱船上进行了实船应用验证。船舶装载时,根据本航次载货量和计划航速状况通过阻力与纵倾角间的数学模型可得到船舶的最佳纵倾角,按此最佳纵倾角指导船舶装载,使得航行时船舶阻力最小,从而实现较低燃油消耗。按照最佳航态指导船舶营运后,航次燃油节省3.5%以上,起到了良好的效果,对提升船舶产品内在竞争力,具有积极的社会效益和经济效益。

