HPM微课在初中数学教学中的实践研究

    王亮 王书荣

    

    

    

    摘? 要 研究通过微课将数学史教学资源渗透进课堂教学，通过数学史教学激发学生的数学学习兴趣，拓展其数学思维。

    关键词 HPM;微课;初中数学;数学史;核心素养

    中图分类号：G633.6? ? 文献标识码：B

    文章编号：1671-489X（2020）05-0115-03

    1 前言

    新课程标准下的初中数学教学，提出了核心素养模式下的教学理念，其中就包括数学史知识的学习。在日常教学中，由于教学任务繁重和应试教学目标的影响，数学史资源没有很好地在初中数学教学中展开。教材中对数学史知识的陈述，大都是通过拓展阅读材料来呈现，不仅学生很容易忽视，就连教师也只要求学生课后自己阅读。大段的文字叙述，对于理解能力较弱的初中生来说具有一定困难。探索数学史呈现的方式，成为新课改背景下初中数学教学的一大任务。

    HPM是History and Pedagogy of Mathematics的缩写，意思是数学史和数学教学的融合。HPM微课是将数学史和微课融合，以数学史为主线，结合数学知识制作微课，通过简短的微课为学生呈现数学知识的发现过程，激发学生学习数学知识的兴趣。在新知识的学习过程中，以数学史作为辅助学生学习的载体，能够培养学生的探究能力[1]。

    2 HPM微课在初中数学教学中应用的意义

    化枯燥为形象? 初中数学教材所呈现的文本式数学史知识，让学生感到枯燥无味，而教师由于教学时间紧张，很少会有意识地为学生讲解数学史知识。数学史是一部数学发展的历史。如果通过微课视频将数学史呈现给学生，教师在课堂上通过播放数学史来向学生讲解数学知识，生动和趣味的数学史故事很快就能够激发学生的学习兴趣。同时，科学家的探索历程也能够调动学生的思维，让学生按照科学家的思路去学习新知识。比如关于笛卡尔发明直角坐标系的数学史：

    笛卡尔一天卧病在床，思考怎样将直观的几何知识和抽象的代数概念相融合。直到他发现一只蜘蛛在墙角，上下左右跳动着织网，于是产生灵感：是否可以以墙面为参照物来表示蜘蛛的位置？随后他结合两条垂直的墙线发明了直角坐标系，通过几何坐标将平面上任意位置表示出来。

    学生发现原来蜘蛛网也是数学知识发现的源泉，生动形象的数学史瞬间激发了学习兴趣。

    从课堂点缀到主动学习? 传统课堂上数学史只是作为课堂点缀的内容，教师通过图片或者口头向学生介绍数学家的简介和精神品质。但是在学生眼中，数学史就是课外知识，很少会有学生认真对待。HPM微课将知识教学和数学史相结合，在课前导入、课中教学、课后拓展中融合知识与数学史，同时可以以数学史作为新知识呈现的载体。

    如在讲授“一元一次方程”时，教师可以将《九章算术》中的“盈不足术”内容展示给学生。其中有一个关于一元一次方程的题目情境：今日有人买羊，人出五，不足四十五;人出七，不足三。要求学生求出人的数量和羊的价格分别为多少？本题和教学内容紧密相连，在新课授课的过程中，教师可以将数学史作为新知识分析的过程，引导学生通过分析历史资料，对其中的数学问题进行深入研究，在教师的指点下理解知识。因此，数学史成为新知识的载体，是新课教学的重要部分，不再是课堂点缀内容，引起学生对数学史的重视。

    在课后拓展中向学生呈现数学史知识，将数学史作为课后学习任务，要求学生在小组学习过程中通过数学史自主巩固复习，更进一步地体现了数学史价值，让数学史成为引导学生课后学习的途径。

    3 HPM微课在初中数学教学中的实践研究

    课堂导入中的实践研究? 对于刚进初中的学生来说，很多数学名词是非常陌生的，比如无理数、函数、坐标、元等。对于这些新颖的数学名词，学生常常会出现理解错误，甚至在课堂上答非所问，不理解其中内涵。如在讲解“无理数”时，班上有学生学习完无理数概念后，还不能区分无理数和有理数;有的学生甚至还认为无理数是有理数中的小数。对于这种现象，教师在课堂导入过程中通过HPM微课引导学生观看故事，首先对无理数和有理数的区分有一个大致的了解，有助于在新课讲解中理解无理数的概念。

    教师展示的是关于希帕索斯发现无理数的数学史：

    古希腊数学家毕达哥拉斯认为世间所有的事物都可以用数字来表示，1是所有数字的生成元素，用数字表示世间万物的方法，要么是用1的倍数来表示，要么是通过将两个1的倍数进行比较，从而用比值来进行表示。毕达哥拉斯的理论受到数学界的广泛重视。随着勾股定理的提出，毕达哥拉斯的学生希帕索斯在研究勾股定理时发现，将直角三角形的两条直角边确定为1的时候，那么斜边的平方为2，即两个1的平方之和，但是无法按照毕达哥拉斯的定理，在自然界中找到一个整数或者两个整数的比值来表示斜边的长度。他大胆地打破权威，认为在有理数范围内无法找到相应的数，并用“”表示斜边长度。从此，世界上第一个无理数诞生了。

    由此爆发第一次数学危机，支持毕达哥拉斯定理的人为了捍卫权威，将希帕索斯扔进大海。直到1000年后，人们发现了这一类数，并且被达·芬奇命名为“无理数”。

    从充满神秘和封建权威色彩的数学史中，学生认识到无理数是存在于有理数范围之外的数，既不能用整数来表示，也不能用比例来表示，并由“”为例可以在头脑中初步形成无理数概念的轮廓。

    新课讲授中的实践研究? 数学史知识表面上是历史类知识，看似和新知识没有很大关联，但是仍然可以作为新知识讲授的载体。比如函数问题、三角形几何证明、路程速度类应用题，都是学生感到非常困难的专题，如果教师整堂课通过大量的例题进行讲解，学生很容易感到枯燥，丧失学习兴趣;如果教师导入HPM微课，穿插扣人心弦的数学史故事，那么学生的学习兴趣将会很快被激发。

    如在讲授“一元一次方程的应用”时，教师可以将丢番图的墓志铭作为微课教学的数学史内容（图1），这是丢番图临终前为自己的年龄所设计的墓志铭。数学史微课视频中向学生详细介绍丢番图一生中经历的重要事情及其时间段，要求学生当一回考古学家，通过一元一次方程对这位数学家的去世年龄进行一次计算。本次新课讲解与以往不同的是，将数学问题融入故事中，对于好奇心强、喜欢推理类故事的初中生来说是一个非常好的学习素材。因此，学生非常积极地展开探索，在教师引导下，很快就有學生寻找到本题的未知数，应该是设丢番图的年龄为x，根据题意分析丢番图在幼年、青年、成年的时间和一生的时间之间的数量关系可以列出方程：

    （1/6）x+（1/12）x+（1/7）x+（1/2）x+5+4=x

    最后解得丢番图活了84岁。在具有推理色彩的数学史故事中，学生的学习积极性和探索欲望会更加强烈，再加上教师的引导，学生懂得解决一元一次方程的应用题，要先从数量关系中寻找设未知数x的量。比如本题中“他的生命的1/6”，学生就应该思考是否可以将生命的年限作为未知数呢？最后让学生列出完整的一元一次方程并求解。

    知识拓展中的实践研究? 在传统教学中，教师都会留出几道思考题让学生课后思考，作为拓展学生思维的方式。但是由于学生的学习压力大，再加上题目不能激发学生的兴趣，导致知识拓展教学展开得并不顺利。

    在HPM微课中渗透数学史知识，可以将原本形同虚设、无人关注的数学史阅读材料作为打造第二课堂的主要素材。如在教学完“整式的乘除”后，教师将“杨辉三角”作为数学史微课教学的主要题材。学生学习完本节内容后，对于（a+b）2、（a+b）3很容易能够展开，但是如果出现（a+b）4、（a+b）5，或者次方数更加大的时候，就束手无策了。

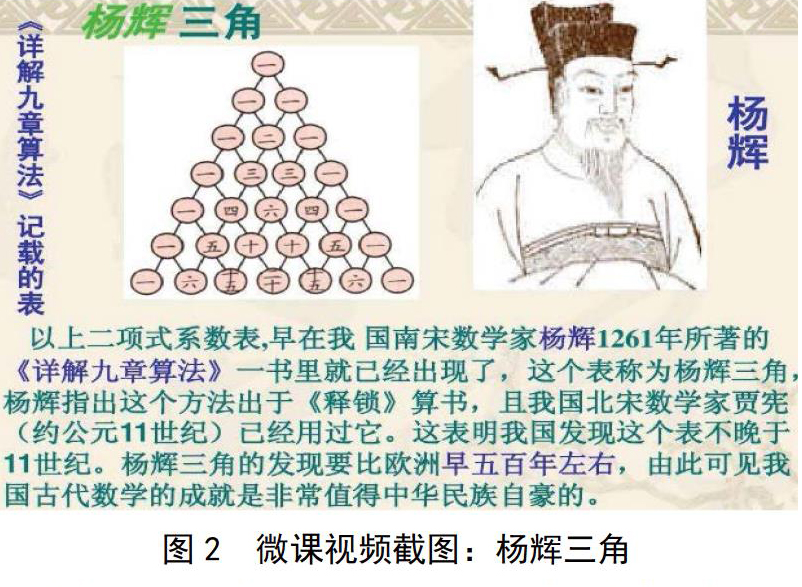
    为了帮助学生化解问题，拓宽学生知识面，在数学史微课中，首先展示的是一位教师非常流利地写出展开式（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5，学生看到后非常惊讶。细致的学生发现展开式中a的次方逐渐递减，而b的次方逐渐递增;对于展开式中各项的系数，却没有发现任何规律。随后，教师要求学生继续观看视频，微课视频开始介绍我国著名数学家杨辉的生平事迹，以及他对我国数学的主要贡献——“杨辉三角”，如图2所示。

    学生通过观察发现，三角形两条斜边上的数字永远是1，每一行的中间的数字是上一行与其相对应的左右两个数字之和，三角形顶端数字为20，第一行为21，第二行为22，以此类推，第n行为2n。学生找出规律后，教师试着要求学生将整式（a+b）n和2n相联系。学生除了發现当a和b均为1时两式相等之外，结合“杨辉三角”还发现，（a+b）n

    展开后的各项系数和“杨辉三角”第n行的数字一模一样。比如（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5中，各项系数为1、5、10、10、5、1，正好是“杨辉三角”中第五行的数字。

    通过本次数学史微课教学，学生的思维得到拓展，学会了结合“杨辉三角”将（a+b）n展开的方法。

    4 结语

    数学史是融合数学家探索精神和知识形成过程的资料，而微课以其简短精练的特征，可以有效开展针对性教学。本次研究探索了将数学史和微课融合后的HPM微课教学，将HPM微课融入教学各个阶段，从而有效激发学生的学习兴趣，拓展学生思维，让初中数学课堂更加高效。

    参考文献

    [1]罗建国.基于HPM视野，让数学史与学生美好相遇[J].江西教育，2019（24）：69.

    作者：王亮，淄博市周村区王村中学，二级教师，周村区教学先进个人，周村区优秀班主任，研究方向为中小学数学;王书荣，淄博市周村区王村中学副校长，一级教师，研究方向为中学数学（255300）。