如何在几何定理教学中培养作图能力

    张艳 洪燕

    

    

    

    摘? ?要：作图能力的培养需要一定的实践，这种实践一方面可以通过完成有针对性的习题，在习题讲练的过程中获得，另一方面可以通过新授课中对一些定理的探究，动手作图中获得.通过三节几何定理课教学片断的展示，初探如何在几何定理探究与证明的教学过程中引导学生重视作图顺序，避免画图时过度添加条件以及利用图形的构造增强学生的几何直观.

    关键词：几何直观;定理教学;作图顺序;图形构造

    培养学生的作图能力，可以增强学生的几何直观，发展空间观念，从而提升学生在直观想象方面的数学素养[ 1 ].近几年的中考试题命制越来越注重作图能力的考查，然而当题目没有图，或者题目中涉及到图形的构造时，学生作图意识和作图能力是非常薄弱的.在几何习题课教学中，常见到教师通过有意识的引导学生自己画图，培养作图意识，或者通过习题点评，培养学生的作图能力.而在几何定理教学中，却因为侧重于定理的论证与应用，而忽略了作图能力的培养.笔者在教学过程中，发现一些几何定理在探究和论证时都能很好的培养学生作图，并能发现和纠正学生在作图中易犯的错误.下面将用三个几何定理探究与证明的教学案例来具体阐述如何在课堂教学中渗透作图意识，提高学生的作图能力.

    1? 对角线相等的平行四边形是矩形

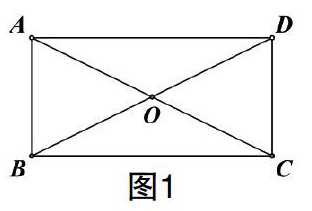
    例：（人教版八下18.2.1矩形）教师要求先写出已知，求证，并请一位学生上台演示如何画图;学生很快写出了已知：如图1，在ABCD中，AC=BD，求证：ABCD是矩形.但在画图中却遇到了问题：学生一开始先用直尺画出线段AD并记录它的长度，然后拿直角三角板的一条直角边靠着AD，沿另一边画出AB，再用推平行线的方式画出BC，且保证了BC=AD;最后连接DC.这种画法虽然能得到已知条件AC=BD，但在画的过程中实际已经用到了∠BAD=90°，也就是默认了ABCD是矩形.第二种画法学生先画一个任意的平行四边形，再连对角线AC，BD，发现又保证不了AC=BD.该如何严格根据已知条件作出图形呢？学生陷入了沉思……

    教师引导学生思考可否在画图时将已知中的两个条件ABCD和AC=BD颠倒顺序，先画AC=BD，再连接A，B，C，D四点，得到平行四边形;学生在操作时发现颠倒顺序后，不仅要画出两条相等的线段AC，BD，且这两条相交线段还需要互相平分，这样才能保证连出的四边形ABCD是平行四边形。从而成功的画出了该命题的图象.

    在学生独立作图时，正确的作图顺序是成功作出图形的关键.此定理教学中利用矩形判定1的准确作图，让学生意识到命题证明的作图是需要严格遵照已知条件的，既不能随意添加，也不能缺漏，更不能直接将结论在图形中画出来.当作图遇到困难时，适当调整作图顺序，可能问题就能迎刃而解.

    2? 四条边都相等的四边形是菱形

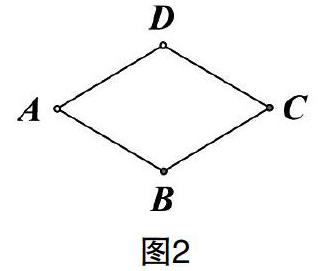
    例：（人教版八下18.2.2菱形）教师要求学生写出已知，求证，并画图;学生迅速写出了已知：如图2，AB=BC=CD=AD，求证：四边形ABCD是菱形;并画出了一个如图2的形似菱形的四边形;这四条线段是否相等很含糊，因此针对画图过程师生有了以下对话：

    师：画的四边形中四条线段看起来的确很像等线段，这是怎么做到的呢？

    生：用尺子量的;

    師：那我们来试一试，每条线段都按2cm的长度，看看是不是真能画出这么像的图形？

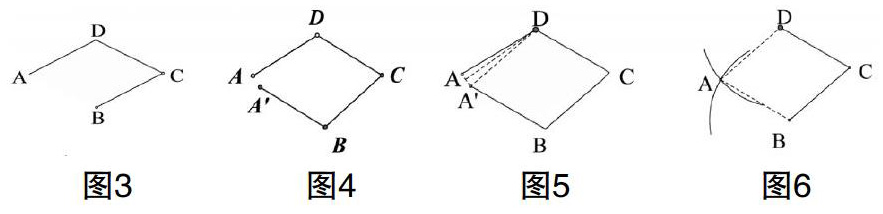
    教师拿出尺子画出了三条2cm的线段，AD，DC，BC，然后停了下来（图3），问：第四段怎么画？

    生1：连接AB;

    师：那怎么能保证线段AB的长也是2cm呢？

    生2：以B为端点画线段AB等于2cm.

    师：以B为端点画出的2cm线段怎么能保证另一个端点就刚刚好落在A处呢？你看我就能画出另一端点不在A处的图（图4）;

    在这段对话中，教师纠出了学生在作图中常见的错误——条件过多：既要连接AB，又要求线段AB长度为2cm，这种错误主要出现在几何题添加辅助线时。避免这个错误关键看作辅助线涉及到的点的个数，若是有两个点，则作图中连接两点后就不能再额外要求这条线段有其他位置关系或数量关系.

    纠错之余，如何准确的画出该命题的图呢？还需要另一个画图工具——圆规.教师继续引导：（1） 如果图5中的点A会动，把它移动到A'的位置就好了，问题是怎么挪A？满足条件的点A移动轨迹应该是怎样的？（2） 在纸上可以用什么画图工具来实现这种移动？学生通过思考发现点A的轨迹应该是一个圆.因此可以利用圆规描出点A的轨迹，同时点A所在的这段弧可能与线段A'B没有交点，因此再次利用圆规以B为圆心，2cm的长度为半径，画弧，A'点就在这段弧上;而这两段弧的交点就满足到点D和点B的距离都是2cm.（图6）

    教师总结：当圆规的张角不变时，所画圆的半径不变。那么即使圆心变了，所画弧上任意一点与对应圆心的连线长度依旧相等，即两弧交点到两个圆心的距离也相等.由此可以看出圆规是刻画相等线段一个很好的工具.

    3? 角平分线性质的探究

    探究任务：（1）在纸上画∠AOB，并画出角平分线OC，在OC上取一点P;（2）利用圆规，直尺或量角器等数学工具，在OA和OB上各找一个点M，N，使△OMP≌△ONP;

    学生利用刻度尺、圆规、量角器进行作图.教师从旁收集到了两种构造方法：

    第一种构造：利用圆规在角两边截取OM=ON ，并连接MP，NP.（图7，8）构造两个三角形全等的理由是SAS.

    第二种构造：利用量角器，以点P为顶点，OP为一边量取∠OPM=∠OPN等于某个度数（任意），交OA，OB于M，N.（图9，10）全等理由ASA.

    从学生的画法上看，两种构造，一种是构造边等，一种是构造角等，教师引导学生思考是否有遗漏：1.从构造边等来看，除了构造OM=ON，能不能构造MP=NP呢？2. 从构造角来看，除了取∠OPM=∠OPN，能不能取∠OMP=∠ONP呢？

    学生通过小组讨论得出：第一个角度构造MP=NP行不通，因为这样得到的三个条件MP=NP，一条公共边OP，∠AOC=∠BOC组合成了SSA，不能判定三角形全等;第二个角度从理论上是可以利用AAS得到两个三角形全等，但在实际操作时却发现画不出来.追问原因，原来是在OB上任取点N时，∠ONP的大小任意，利用量角器量出∠ONP的度数，也无法用量角器画出相同度数的∠OMP，因为图中仅仅只有∠OMP两边上的点P，O，∠OMP的顶点M找不到.

    教师继续引导：如果普通的∠ONP画不出对应的等角∠OMP，可以考虑一些不用量角器能画出来的特殊的角度。 学生再次动手操作，这次个别学生用上了三角板，发现当利用三角板的两条直角边，可以很容易画出∠OMP=∠ONP=90°，这样构造出两个全等的直角三角形（图11）.三种构造方式，画出的全等三角形既有锐角，又有直角，钝角。特别地，对于全等的直角三角形，MP和NP还有一个特殊的身份：垂线段.过点P作一直线的垂线段，这条垂线段的长度可称为点到直线的距离。因此MP和PN的长度可表述为点P到角两边的距离.通过刚才的构造，可知无论P点位于角平分线的何处，MP与NP总是相等的.也就是说，命题“角平分线上的任意点P，到角的两边距离都相等”是真命题，我们将这一真命题又称为角平分线的性质.

    角作為几何图形的基本组成元素，本身是一个轴对称图形，其对称轴是角平分线所在的直线.在探究角平分线的性质时，构造全等的过程及全等图形的汇总，促进了学生对角轴对称这一性质的几何直观认知，在今后的解题中，若出现图11这样的基本图形结构，能迅速反应到三角形全等上，收获更多的边角关系，对开拓解题思路，提高解题速度有很大的帮助.

    4? 小结

    任何一种能力的培养都必须以教材为依据，分析教材、了解教材编排意图，才能有效地完成发展学生能力的任务[ 2 ]。学生在初次接触一个新定理时，给予其完整的探究，并在论证定理时将已知、求证、画图留给学生自己完成，能够很好启发学生的创新意识，诱发学生的求知欲，培养自主学习的能力，从而达到提高学生数学素养的目的。

    参考文献：

    [1]范林伟.发展核心要素 提升作图能力[J].辽宁教育，2014（19）：36-37.

    [2]廖芬顺.培养小学中年级学生几何直观能力的策略研究[J].亚太教育，2019（6）：79-80.