正方体平面展开图中重合点的判定方法
我们知道,将正方体展开成平面图形有多种方法,但是将这些展开图恢复成立体图形,其重合点如何判别?下面提供一种有效快捷的方法供同学们参考.
为了叙述方便,我们先给出“拐点”一词的定义:在正方体平面展开图中,两个正方形仅有一个公共顶点的点称作平面展开图中的“拐点”.
例如图1中,N、Q、D是拐点.

图1
如何判断正方体平面展开图中的重合点呢?其方法可以归纳成两句话:“拐点”两旁各自站,重合点后对应排.
下面我们来看两个实例.
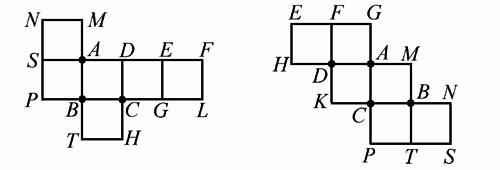
图2 图3
例1 如图2,是一个正方体的平面展开图,找出图中各点对应立体图形的重合点.
分析 1.拐点为A、B、C.
2.拐点两旁各自站. (在两个拐点之间的点)
如拐点A两旁的点分别为:一旁为M、N、S、P;另一旁为:D、E、F、L.
3.重合点后对应排.
拐点A与自身重合. 则M与D、N与E、S与F、P与L重合.
同理:P与T、H与G重合. (注意P、T、L为三点重合)
解 正方体共有8个重合点,分别为:
A、D(M)、E(N)、F(S)、P(T、L)、B、G(H)、C.
例2 如图3,是一个正方体的平面展开图,找出图中各点对应立体图形的重合点.
分析 1.由A、B、C、D四个点为拐点,G、M、N重合一点;H、K、P重合一点.
2.重合点后对应排.
G、M、N重合后,与其相邻的点分别为F与S,F与S重合. 同理,E与T重合.
解 本题中对应立方体的重合点为:A、B、C、D、G(M、N)、H(K、P)、F(S)、E(T).
为帮助同学们加深理解,请做以下两个练习. 如图4、5,请分别写出对应的立体图形的重合点.
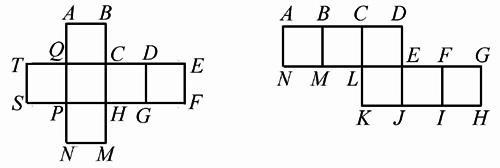
图4 图5
参考答案 图4:B(D)、A(E、T)、S(N、F)、M(G)、C、H、P、Q;图5:D(F)、C(G)、B(H)、M(K)、N(J)、A(I)、L、E.
作者简介:谢中炳,男,1958年6月生. 湖北省黄石市下陆中学党支部书记,中学数学高级教师,主要研究初中数学教与学. 在《数学辅导报》、《小博士报》、《学习报》等报刊发表教学论文10余篇.
为了叙述方便,我们先给出“拐点”一词的定义:在正方体平面展开图中,两个正方形仅有一个公共顶点的点称作平面展开图中的“拐点”.
例如图1中,N、Q、D是拐点.

图1
如何判断正方体平面展开图中的重合点呢?其方法可以归纳成两句话:“拐点”两旁各自站,重合点后对应排.
下面我们来看两个实例.

图2 图3
例1 如图2,是一个正方体的平面展开图,找出图中各点对应立体图形的重合点.
分析 1.拐点为A、B、C.
2.拐点两旁各自站. (在两个拐点之间的点)
如拐点A两旁的点分别为:一旁为M、N、S、P;另一旁为:D、E、F、L.
3.重合点后对应排.
拐点A与自身重合. 则M与D、N与E、S与F、P与L重合.
同理:P与T、H与G重合. (注意P、T、L为三点重合)
解 正方体共有8个重合点,分别为:
A、D(M)、E(N)、F(S)、P(T、L)、B、G(H)、C.
例2 如图3,是一个正方体的平面展开图,找出图中各点对应立体图形的重合点.
分析 1.由A、B、C、D四个点为拐点,G、M、N重合一点;H、K、P重合一点.
2.重合点后对应排.
G、M、N重合后,与其相邻的点分别为F与S,F与S重合. 同理,E与T重合.
解 本题中对应立方体的重合点为:A、B、C、D、G(M、N)、H(K、P)、F(S)、E(T).
为帮助同学们加深理解,请做以下两个练习. 如图4、5,请分别写出对应的立体图形的重合点.

图4 图5
参考答案 图4:B(D)、A(E、T)、S(N、F)、M(G)、C、H、P、Q;图5:D(F)、C(G)、B(H)、M(K)、N(J)、A(I)、L、E.
作者简介:谢中炳,男,1958年6月生. 湖北省黄石市下陆中学党支部书记,中学数学高级教师,主要研究初中数学教与学. 在《数学辅导报》、《小博士报》、《学习报》等报刊发表教学论文10余篇.

