工业机器人误差建模与分析

2024.03.10

梁睿李冬英李斌王蒙宽

摘?要：当前工业机器人重复定位精度高，一般都能达到0.01mm以下，绝对定位误差精度较低，比重复定位精度高了1-2个数量级，成为了制约工业机器人发展应用的主要因素，首先利用矩阵法建立工业机器人误差模型，再利用Monte Carlo数值仿真法，运用控制变量法研究各连杆参数误差对机器人末端位置的影响，仿真结果表明，前三关节的关节转角误差和连杆扭角误差对末端位置误差起到主导作用，其余參数误差可以忽略不计。

关键词：工业机器人;绝对定位精度;误差模型;矩阵法;误差分析

影响工业机器人绝对定位精度的因素种类繁多，但运动学参数误差因素对绝对定位精度的影响最大，占80%以上[1，2]。因此要提高绝对定位精度，首先需要对运动学参数误差进行误差分析，从而针对性优化机器人结构，提高绝对定位精度[3]。本文以ROKAE公司的XB4型6R工业机器人为研究对象，研究运动学参数误差对机器人绝对定位精度的影响。采用Denavit-Hartenberg法建立机器人正运动学模型。在此基础上，通过矩阵法推导并建立机器人连杆参数误差模型。基于该模型，使用Monte Carlo数值进行仿真，研究各连杆参数误差对对机器人绝对定位精度的影响。

1 建立误差模型

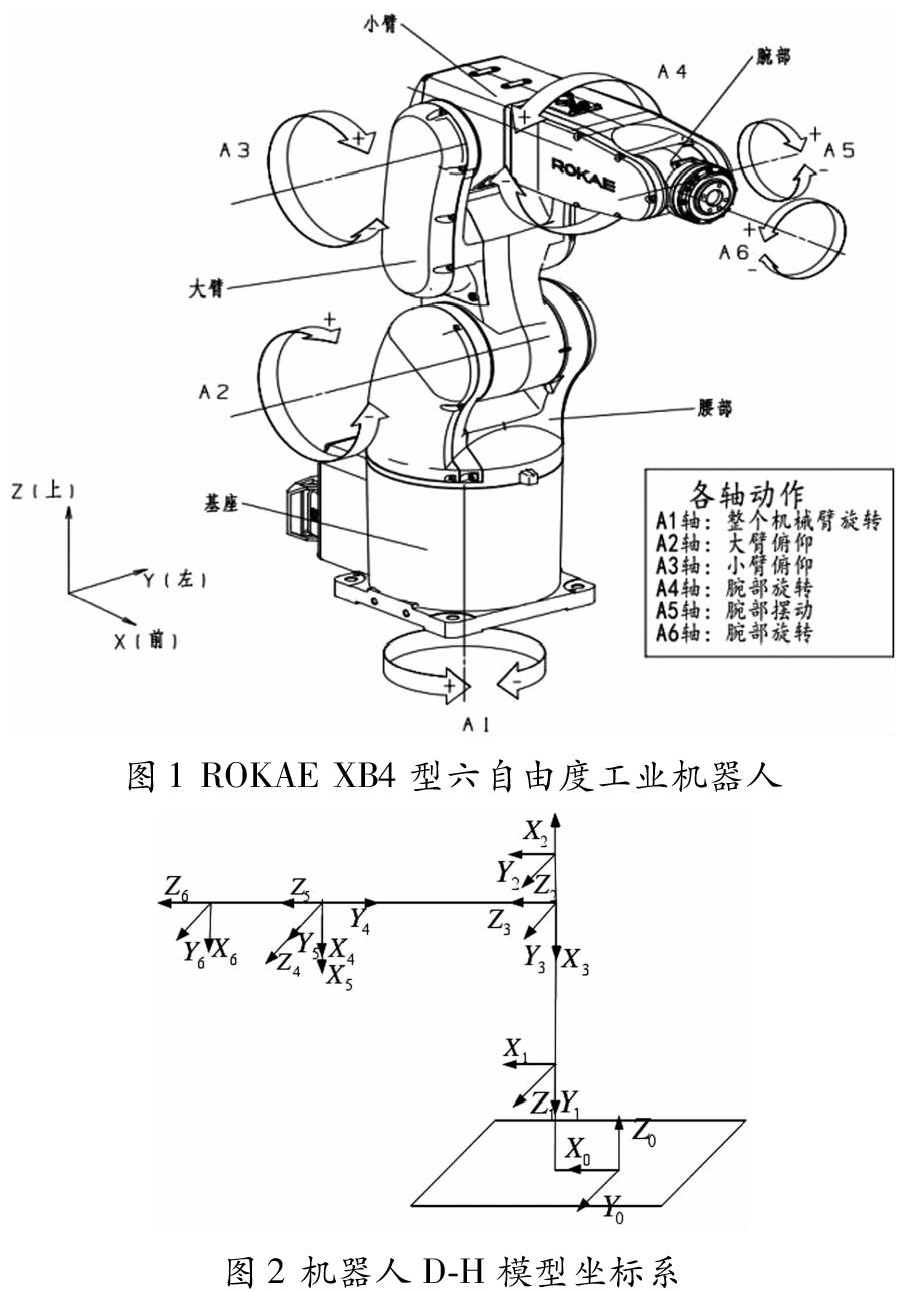
本文研究对象为六自由度工业机器人如图1所示，运用DH法建立的模型坐标系如图2所示。

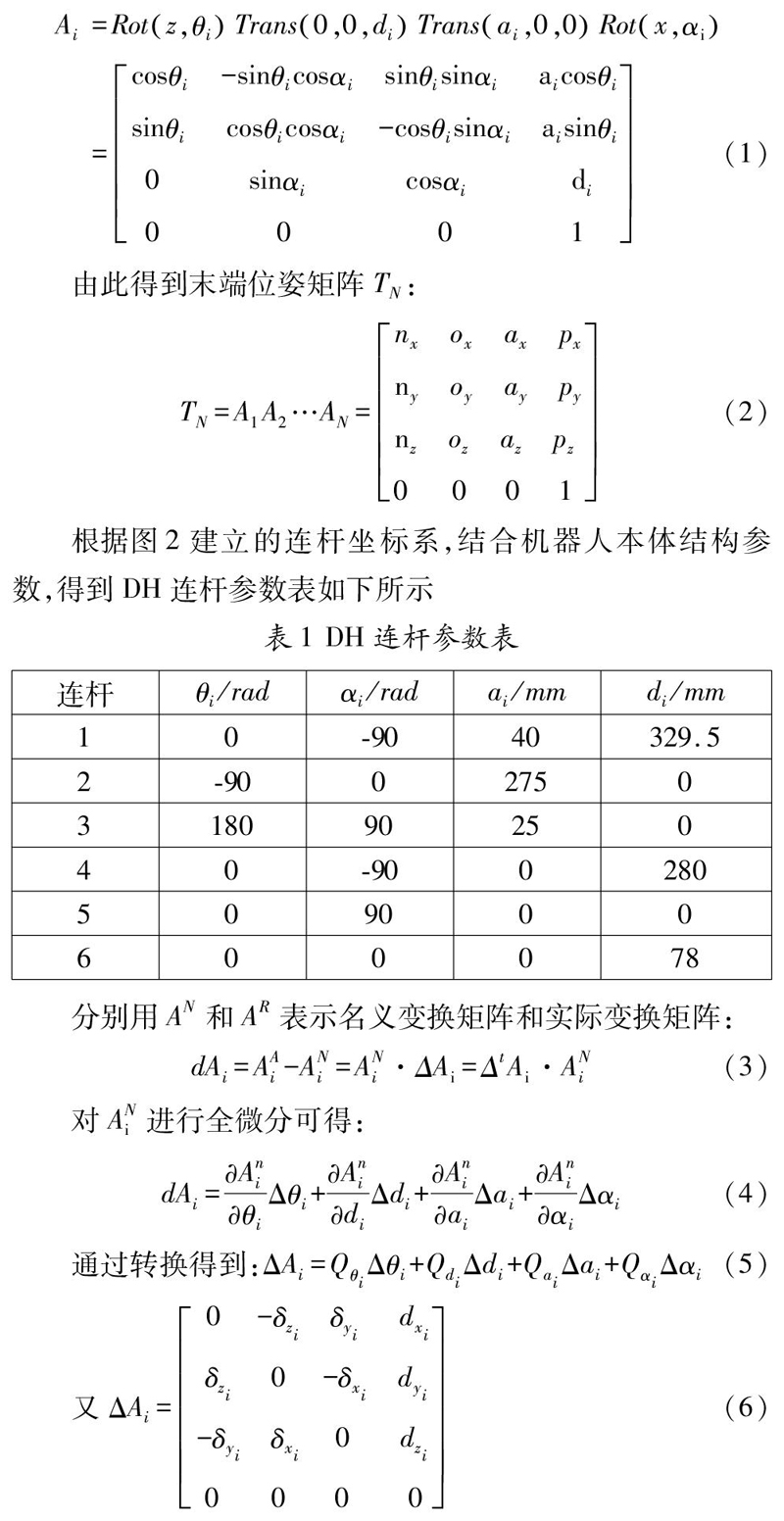
DH建模法的具体理论限于篇幅不详细阐述，仅列出其关键要素，根据DH法建立起相邻关节坐标系的变化矩阵：

由此得到末端位姿矩阵TN：

根据图2建立的连杆坐标系，结合机器人本体结构参数，得到DH连杆参数表如下所示

分别用AN和AR表示名义变换矩阵和实际变换矩阵：

其中D表示基于基坐标系的末端执行器微分运动列矢量，Di表示基于第i关节坐标系的末端微分运动列矢量，该式即为机器人运动误差传递模型。

2 机器人误差参数仿真分析

根据表1数据和式（11）误差模型使用matlab进行分析，将得到的末端位置误差运用Monte Carlo法分别在各误差参数独立作用与各误差参数共同作用进行仿真，统计样本为10000次。在进行误差源单独作用仿真时，将所有的连杆参数误差统一设置为0.001，计算单个误差占总误差的百分比，将其定义为独立作用下的贡献指数，结果为图3所示。在进行误差源共同作用下仿真时，先将所有误差参数统一设置为0.001，求出所有参数共同作用下的误差，再将目标误差参数的误差值设为0，其余不变，计算去除单独误差参数后的误差，计算前后误差的差值，将每个参数的误差相加得到总误差，计算单个误差占总误差的百分比，将其定义为共同作用下的贡献指数，结果为图4所示。

由图3、图4可知，各参数独立作用和共同作用下，连杆长度和连杆偏距的误差均远小于关节转角和连杆扭角，对末端位置的影响可以忽略不计;一二三关节的转角、扭角对末端误差影响明显大于四五关节。

3 结语

本文以6R工业机器人为研究对象，基于矩阵法推导出串联机器人误差参数模型，运用Monte Carlo法分析了独立作用下和共同作用下各类误差参数对末端位置误差的影响，仿真结果表明，长度类参数和后三关节角度类参数对末端位置影响非常有限，一般可忽略不计。要提高绝对定位精度，重点要提高前三关节角度参数精度。

参考文献：

[1]王田苗，陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报，2014，50（09）：1-13.

[2]叶声华，王一，任永杰，李定坤.基于激光跟踪仪的机器人运动学参数标定方法[J].天津大学学报，2007（02）：202-205.

[3]唐尧，张恩政，陈本永，陈刚，刘翠苹.基于运动学分析的工业机器人轨迹精度补偿方法[J].仪器仪表学报，2020，41（03）：175-183.

[4]喻敏.工业机器人精度评估与误差补偿研究[D].南京航空航天大学，2015.

[5]陈鹏.基于改进四阶矩的机器人运动可靠性评估方法研究[D].河北工程大学，2020.

[6]徐昌军.基于MDH模型的工业机器人运动学标定技术的研究[D].哈尔滨工业大学，2017.

基金项目：邵阳学院研究生科研创新项目（CX2019SY026）