直角建构 线段求值
薛钧东
【内容摘要】直角(垂直)为条件的线段求值问题经常在中考试题特别是压轴题中出现。该文结合初中数学新课程教学实践,以近几年中考中出现的相关试题为例,说明直角条件与勾股定理、相似三角形、三角形三边关系内在联系的意义建构,以说明线段求值问题的解题思路和方法。
【关键词】初中数学 平面几何 直角建构 线段求值
《义务教育数学课程标准》在教学建议中明确提出:“数学知识的教学,应注重学生对所学知识的理解,体会数学知识之间的关联。”①教师在日常教学中,不但应有效揭示数学知识的数学实质及其体现的数学思想,还应帮助学生理清相关知识之间的区别和联系。直角(垂直)是初中几何的重要内容之一,因为以直角为载体的试题可考查学生的多种能力,所以成为各地中考试题的热点之一,又因其具有很强的综合性,所以能增强中考试题的区分度。如,以直角(垂直)为条件的线段求值问题学生往往不知所措,不知直角与线段用什么知识联系起来,从而形成解题思维中断,导致解题思维障碍②。要帮助学生有效疏通障碍,就要让学生学会意义建构。所谓意义建构就是要指导学生对当前学习内容所反映的事物的性质、规律及该事物与其他事物间的内在联系达到深刻的理解,获得举一反三、融会贯通的教学效果。下面结合初中数学新课程教学实践,以近几年中考中出现的相关试题为例,说明直角条件与勾股定理、相似三角形、三角形三边关系内在联系的意义建构。
一、直角条件与勾股定理内在联系的意义建构
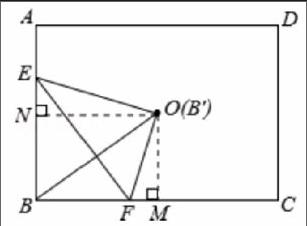
案例1:如图1,点O为矩形ABCD 的对称中心,AB=10cm,BC=12cm,点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s。当点F到达点C(即点F与点C重合)时,两个点随之停止运动。在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F运动的时间为t(单位:s)。是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由。
图1
分析:假设存在实数t能使点B' 与O重合。由对称性可得△EBF≌△EOF,即OF=BF、OE=BE。但等线代换图上没有直接我们所需要的Rt△,此时可通过对称得到相等线段的一个端点(不是公共点)作另一线段的垂线段来构建我们所需的Rt△。即过点O作OM⊥BC于点M,则在Rt△OFM中,OF=BF=3t,FM= BC-BF =6-3t,OM=5,由勾股定理得:OM2+ FM2=OF2,即52+(6-3t)2=(3t)2,解得t= 。同理:过点O作ON⊥AB 于点N,则在Rt△OEN中,OE=BE= 10-t,EN=BE-BN=10-t-5=5-t,ON=6,由勾股定理得:ON2+EN2= OE2,即62+(5-t)2=(10-t)2,解得t=3.9。∵ ≠3.9,∴实数t不存在。
反思:关于直角三角形、矩形一次折叠问题在近几年的中考中频频出现,这类问题能考查学生的数学思维、空间想象和综合解题能力。快速正确解决这类问题的关键就是根据已知条件,通过直角(垂直)来建构合适的Rt△,并运用勾股定理建立只含一个字母的等式。案例1解决的关键是通过折叠得到的有公共端点相等线段的一个端点(不是公共点)作另一线段的垂线段来构建我们所需的Rt△,其特征是一边通过等线代换后能与另一边构成一条新的线段,再利用勾股定理构建方程来解决。
二、直角条件与相似三角形内在联系的意义建构
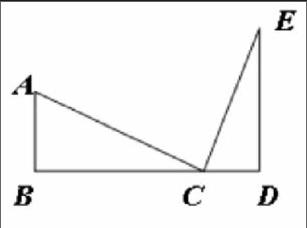
如图2,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠ACE =90°.可得△ABC∽△CDE(证明略)。这是常见的相似图形,因其形似大写的“K”,故称为“K型图”,当出现直角(垂直)条件且与折叠无关时,可通过构建K型图得到相似三角形,再利用相似三角形对应边成比例这一性质就可快速求出线段的长。
图2
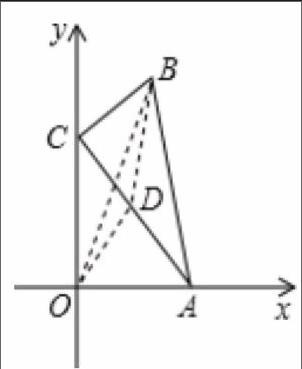
案例2:如图3,已知直线l:y=-x +2与y轴交于点A,抛物线y=(x-1)2 +k经过点A,其顶点为B,另一抛物线y=(x-h)2+2-h(h>1)的顶点为D,两抛物线相交于点C。
(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m①交点C的纵坐标可以表示为:_____或_____,由此请进一步探究m关于h的函数关系式;②如图4,若∠ACD =90°,求m的值。
图3 图4
分析:(1)易得B(1,1),易证点D(h,2-h)在直线l上;
(2)①易知点C的纵坐标为(m -1)2+1或(m-h)2-h+2,可得(m-1)2+1=(m-h)2-h+2,即m= 。
②由于∠ACD=90°,通过直角顶点和两边端点作水平线和竖直线构建K型图,即过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F,可得△ACE∽△CDF,推出AE:EC=CF:DF,又∵C(m,m2-2m+2),D(2m,2-2m),∴AE=m2-2m,DF=m2,CE= CF=m,可求出m= 。
反思:相似三角形是初中数学的重要组成部分,是初中几何中计算线段的主要方法之一,由于它综合其他知识点的能力很强,因此在历年的中考中已越来越突显了它的重要地位。具有直角(垂直)条件但不具有折叠特征的线段求值问题常可通过构建K型图得到相似三角形,再通过对应线段成比例来构建方程求解。若K型图直接在题目中呈现给我们,通过K型图很容易求出答案,但案例2并没直接给出K型图,一般可通过直角顶点的水平线或竖直线(直角两边在同侧)与过直角两边端点的竖直线或水平线构建K型图再进一步求解。
三、直角条件与三角形三边关系内在联系的意义建构
案例3:如图5,△ABC中,∠C= 90°,AC=4,BC=2,顶点A、C分别在x轴、y轴的正半轴上滑动,则点B到原点的最大距离是______。
分析:此类问题的难点是不知从何下手,其关键在于抓住运动中不变的量。本题中定值AC恰为Rt△的斜边,则其中线也必为定值。因此,利用AC中点来构建适当的三角形,为本题提供了解题思路。故取AC中点D,连结OD、BD,计算得OD=2、BD= ,当OD+BD=OB时(即B、D、O在一条直线上),就可求得点B到原点O的最大距离是 。
图5
反思:三角形的三边关系是初中几何中主要的不等关系之一,求线段的最值问题也经常涉及到。解决该类问题的核心是构建恰当的三角形,其关键在于要抓住动点问题条件中提供的及其衍生得到的不变量。案例3这类斜边为定值的问题经常取斜边中点来建构三角形,其特征为两条边为定值,再利用两边之和大于第三边、两边之差小于第三边求最值。
总之,解决直角载体有关的线段求值问题,关键在于根据题设特征,建构与相关知识点的内在联系,并快速找到解题思路,扫清思维障碍,节约解题时间。在解题教学中,教师应教会学生运用替代、转换、推理、演绎、建模等数学基本思想进行思考,增强发现和提出问题的能力、分析和解决问题的能力,获得进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验,达到教是为了不教的目的。
【注释】
① 教育部. 义务教育数学课程标准[S]. 北京:北京师范大学出版社,2011.
② 吴亿峰. 智商、情商和潜智能开发[M]. 广东:广东高等教育出版社,2000:76.
(作者单位:江苏省苏州市第一中学分校)



【内容摘要】直角(垂直)为条件的线段求值问题经常在中考试题特别是压轴题中出现。该文结合初中数学新课程教学实践,以近几年中考中出现的相关试题为例,说明直角条件与勾股定理、相似三角形、三角形三边关系内在联系的意义建构,以说明线段求值问题的解题思路和方法。
【关键词】初中数学 平面几何 直角建构 线段求值
《义务教育数学课程标准》在教学建议中明确提出:“数学知识的教学,应注重学生对所学知识的理解,体会数学知识之间的关联。”①教师在日常教学中,不但应有效揭示数学知识的数学实质及其体现的数学思想,还应帮助学生理清相关知识之间的区别和联系。直角(垂直)是初中几何的重要内容之一,因为以直角为载体的试题可考查学生的多种能力,所以成为各地中考试题的热点之一,又因其具有很强的综合性,所以能增强中考试题的区分度。如,以直角(垂直)为条件的线段求值问题学生往往不知所措,不知直角与线段用什么知识联系起来,从而形成解题思维中断,导致解题思维障碍②。要帮助学生有效疏通障碍,就要让学生学会意义建构。所谓意义建构就是要指导学生对当前学习内容所反映的事物的性质、规律及该事物与其他事物间的内在联系达到深刻的理解,获得举一反三、融会贯通的教学效果。下面结合初中数学新课程教学实践,以近几年中考中出现的相关试题为例,说明直角条件与勾股定理、相似三角形、三角形三边关系内在联系的意义建构。
一、直角条件与勾股定理内在联系的意义建构
案例1:如图1,点O为矩形ABCD 的对称中心,AB=10cm,BC=12cm,点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s。当点F到达点C(即点F与点C重合)时,两个点随之停止运动。在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F运动的时间为t(单位:s)。是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由。
图1
分析:假设存在实数t能使点B' 与O重合。由对称性可得△EBF≌△EOF,即OF=BF、OE=BE。但等线代换图上没有直接我们所需要的Rt△,此时可通过对称得到相等线段的一个端点(不是公共点)作另一线段的垂线段来构建我们所需的Rt△。即过点O作OM⊥BC于点M,则在Rt△OFM中,OF=BF=3t,FM= BC-BF =6-3t,OM=5,由勾股定理得:OM2+ FM2=OF2,即52+(6-3t)2=(3t)2,解得t= 。同理:过点O作ON⊥AB 于点N,则在Rt△OEN中,OE=BE= 10-t,EN=BE-BN=10-t-5=5-t,ON=6,由勾股定理得:ON2+EN2= OE2,即62+(5-t)2=(10-t)2,解得t=3.9。∵ ≠3.9,∴实数t不存在。
反思:关于直角三角形、矩形一次折叠问题在近几年的中考中频频出现,这类问题能考查学生的数学思维、空间想象和综合解题能力。快速正确解决这类问题的关键就是根据已知条件,通过直角(垂直)来建构合适的Rt△,并运用勾股定理建立只含一个字母的等式。案例1解决的关键是通过折叠得到的有公共端点相等线段的一个端点(不是公共点)作另一线段的垂线段来构建我们所需的Rt△,其特征是一边通过等线代换后能与另一边构成一条新的线段,再利用勾股定理构建方程来解决。
二、直角条件与相似三角形内在联系的意义建构
如图2,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠ACE =90°.可得△ABC∽△CDE(证明略)。这是常见的相似图形,因其形似大写的“K”,故称为“K型图”,当出现直角(垂直)条件且与折叠无关时,可通过构建K型图得到相似三角形,再利用相似三角形对应边成比例这一性质就可快速求出线段的长。
图2
案例2:如图3,已知直线l:y=-x +2与y轴交于点A,抛物线y=(x-1)2 +k经过点A,其顶点为B,另一抛物线y=(x-h)2+2-h(h>1)的顶点为D,两抛物线相交于点C。
(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m①交点C的纵坐标可以表示为:_____或_____,由此请进一步探究m关于h的函数关系式;②如图4,若∠ACD =90°,求m的值。
图3 图4
分析:(1)易得B(1,1),易证点D(h,2-h)在直线l上;
(2)①易知点C的纵坐标为(m -1)2+1或(m-h)2-h+2,可得(m-1)2+1=(m-h)2-h+2,即m= 。
②由于∠ACD=90°,通过直角顶点和两边端点作水平线和竖直线构建K型图,即过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F,可得△ACE∽△CDF,推出AE:EC=CF:DF,又∵C(m,m2-2m+2),D(2m,2-2m),∴AE=m2-2m,DF=m2,CE= CF=m,可求出m= 。
反思:相似三角形是初中数学的重要组成部分,是初中几何中计算线段的主要方法之一,由于它综合其他知识点的能力很强,因此在历年的中考中已越来越突显了它的重要地位。具有直角(垂直)条件但不具有折叠特征的线段求值问题常可通过构建K型图得到相似三角形,再通过对应线段成比例来构建方程求解。若K型图直接在题目中呈现给我们,通过K型图很容易求出答案,但案例2并没直接给出K型图,一般可通过直角顶点的水平线或竖直线(直角两边在同侧)与过直角两边端点的竖直线或水平线构建K型图再进一步求解。
三、直角条件与三角形三边关系内在联系的意义建构
案例3:如图5,△ABC中,∠C= 90°,AC=4,BC=2,顶点A、C分别在x轴、y轴的正半轴上滑动,则点B到原点的最大距离是______。
分析:此类问题的难点是不知从何下手,其关键在于抓住运动中不变的量。本题中定值AC恰为Rt△的斜边,则其中线也必为定值。因此,利用AC中点来构建适当的三角形,为本题提供了解题思路。故取AC中点D,连结OD、BD,计算得OD=2、BD= ,当OD+BD=OB时(即B、D、O在一条直线上),就可求得点B到原点O的最大距离是 。
图5
反思:三角形的三边关系是初中几何中主要的不等关系之一,求线段的最值问题也经常涉及到。解决该类问题的核心是构建恰当的三角形,其关键在于要抓住动点问题条件中提供的及其衍生得到的不变量。案例3这类斜边为定值的问题经常取斜边中点来建构三角形,其特征为两条边为定值,再利用两边之和大于第三边、两边之差小于第三边求最值。
总之,解决直角载体有关的线段求值问题,关键在于根据题设特征,建构与相关知识点的内在联系,并快速找到解题思路,扫清思维障碍,节约解题时间。在解题教学中,教师应教会学生运用替代、转换、推理、演绎、建模等数学基本思想进行思考,增强发现和提出问题的能力、分析和解决问题的能力,获得进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验,达到教是为了不教的目的。
【注释】
① 教育部. 义务教育数学课程标准[S]. 北京:北京师范大学出版社,2011.
② 吴亿峰. 智商、情商和潜智能开发[M]. 广东:广东高等教育出版社,2000:76.
(作者单位:江苏省苏州市第一中学分校)

