高中物理力学学习中数学方法的应用解析

    刘长平

    

    

    

    在高中阶段，各个学科之间都存在着一定的联系，数学和物理之间也是如此.通过数学公式和其中相关逻辑思维对力学问题进行学习和解答，可有效提升学生的解题效率和准确性，并且还可提升学生的逻辑思维能力与知识运用能力.

    一、函数在高中物理力学学习中的应用

    物体在时间变化下，各物理量都会存在一定转变，各个量之间会形成简单或复杂的函数关系.如果可以对物体的状态进行明确，那么函数就可转变成为固定量的关系方程.因此，在解答高中物理力学问题时可结合物理过程特点，适当运用函数.经常运用的函数包括二次函数、三角函数，等等.

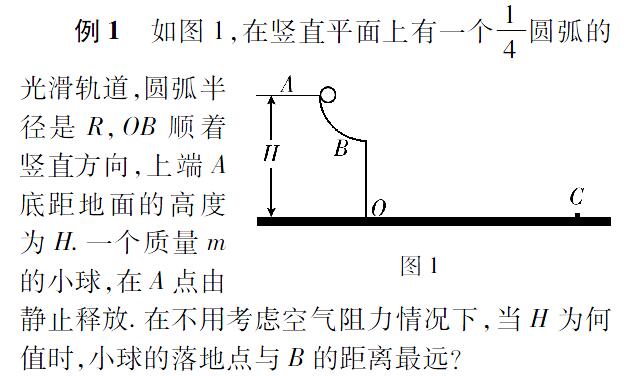
    例1 如图1，在竖直平面上有一个14圆弧的光滑轨道，圆弧半径是R，OB顺着竖直方向，

    上端A底距地面的高度为H.一个质量m的小球，在A点由静止释放.在不用考虑空气阻力情况下，当H为何值时，小球的落地点与B的距离最远？

    在解答该问题时，可以根据平抛运动的规律求出水平距离的表达式，再结合二次函数求极值得出小球的落地点与B的距离最远时H的值.

    二、图像在高中物理力学学习中的应用

    图像和文字相比，具有更加形象和直观的特点.在解答具体题目时，如果可以根据物理情境将问题转变成为函数图像，则可以使力学问题变得易于理解和解决.

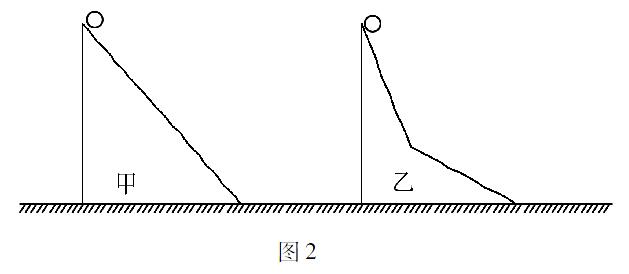
    例2 如图2，已知有甲、乙两个光滑的斜面，两个斜面的长度和高度一致.其中，乙斜面由两部分组成.把两个相同的小球放在两个斜面的顶端，同一时间把小球释放，在不考虑拐角处机械能损失情况下，问：哪个小球先落地？

    解析：甲、乙两个光滑面因为高度相同，且不用考虑拐角处机械能损失，所以两个小球的机械能都处于守恒状态.于是得出两个小球的运动速度是相同的.因为甲、乙两个斜面的倾斜角度不同，通过对两个小球的受力情况进行分析易知，在乙斜面上，小球在前部分的加速度要大于甲斜面小球加速度，而小球在后部分加速度要于甲斜面小球加速度.

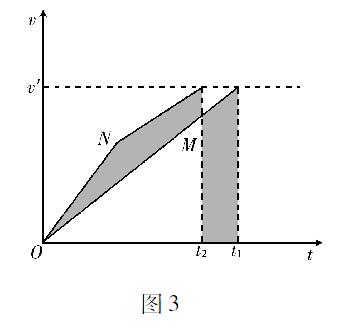
    把乙斜面的两个部分的v-t图像合并以后和甲进行比较如图3所示，由“要让图线与时间轴围成的面积相等”可知，乙斜面小球先落地.

    在解答这类型题目时，通过对运用图像，把物理情境转变成为直观形象的图形，可以有效提升解题效率和准确性.

    三、解析法在高中物理力学中的应用

    一般情况下，物体运动轨迹是结合物理现象和物理实验来观察的，很少有物体运动轨迹是通过理论推导出来的.例如，在斜抛运动中，学生在解答问题时，可以利用数学推导的形式，

    对物体运动轨迹的抛物线进行計算.具体如图4.

    通过分析可知，斜抛运动可以分解为水平方向的匀速直线运动和竖直上抛运动.在水平方向上，抛出的物体以v0x进行匀速直线运动;在竖直方向上，以v0y为初始速度，进行竖直上抛运动.通过分析，不难得出斜抛运动的物体的轨迹方程，且其轨迹属于抛物线.在此基础上，通过数学方法进行观察和推导，可以使学生更加深入地理解和认识抛物运动.

    新课改背景下高中物理力学学习中，应用数学方法非常重要，因为这可以有效提升学生的解题效率和解题准确性，提升学生逻辑思维能力及知识运用能力.因此，在物理教学过程中，教师需结合实际情况，灵活运用数学方法，通过数学公式加深学生对力学知识的理解和记忆，从而学生在高考中获得优异的成绩奠定坚实基础.