二维翼型的积冰数值模拟精度提升方法


摘?要:本文研究并提出了一种可以提升二维翼型积冰模拟精度的方法。采用时间多步法进行冰层增长计算,利用基于流场特征的网格自适应方法,对计算网格进行自适应优化,得到更精确的流场解;利用ALE方法对每个时间步积冰后的机翼外形进行网格重构,为后续时间步流场计算提供更准确的计算网格。最后通过算例验证了这种方法可以有效提升积冰模拟的精确性。
关键词:机翼积冰;ALE;网格重构;数值模拟
飞机积冰后气动性能会明显下降并造成一系列的危害,所以对机翼进行积冰数值模拟研究对于飞行安全有着十分重要的意义。二维翼型的积冰数值模拟计算流程主要分为三步:空气流场计算,得到流场特征结果——基于流场计算结果进行水滴撞击特性计算,得到飞机翼面上的局部水收集系数——利用守恒定理求解积冰热力学模型,得到积冰量以及积冰类型。机翼在积冰形成的过程中,随着冰层积累,外形会发生变化,空气流场也会随之改变,进而影响水滴运动轨迹。因此,二维翼型的积冰数值模拟研究一般采用多步法,即把总的积冰模拟时长分为若干个时间步,每次计算完当前时间步长的积冰冰形后,更新计算网格,然后重复积冰计算的各个步骤(流场、水滴轨迹、冰层增长的计算),直到达到总的积冰时间为止。
1 提升积冰模拟精度的措施
1.1 基于流场特征的网格自适应优化
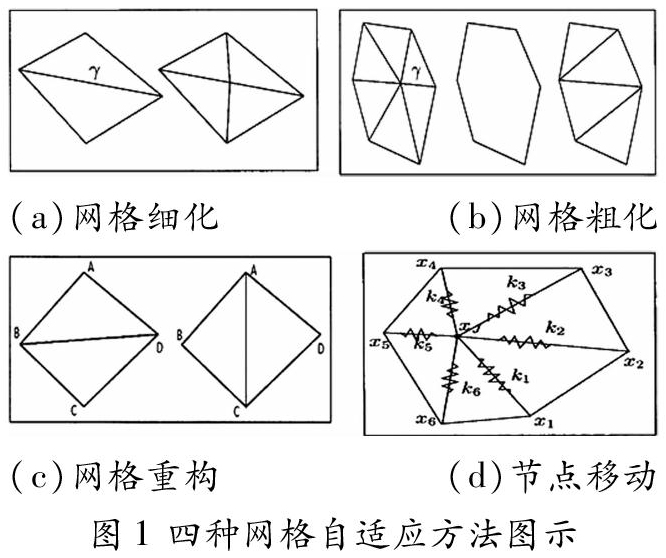
在对翼型进行流场计算时,由于计算网格划分不合理、物面边界网格近似程度低等原因,都会导致计算结果和精确值存在一定的误差[1],为了更好地显示流动特性,需要针对性的对网格进行优化,以减小网格导致的计算误差。基于流场特征的网格自适应优化是指:根据流场计算得到的结果来指定局部网格误差范围,然后按照所需计算值的误差来布置网格节点。如果网格某个区域的误差超过指定范围,则网格需要进行自适应移动,以便针对性地调整网格,从而确定流场与网格的联系,改进流场计算的精度,使得数值解的误差在计算域内接近均匀分布[2]。本文通过结合网格细化、网格粗化、网格单元重构、节点移动这四种自适应的方法来进行网格优化,图1为四种自适应方法的示意图。
网格自适应流程为:(1)首先对网格进行多次节点移动,以得到光顺的边界网格;(2)针对网格曲率较大、质量较差的单元进行网格细化和网格单元重构;(3)根据临界误差值,对计算域进行节点移动、网格细化和粗化、重构等操作,以达到误差要求。
1.2 ALE网格重构法
本文采用ALE重构网格的方法,对积冰后的机翼外形进行网格重构[3]。ALE相关理论详见文献[3]、[4],在这里简要对其进行介绍:如图2,x1、x2为Eule坐标系,它不随物体的运动而改变;X1、X2为Lagrange坐标系,坐标系是固定在物体表面的,物体运动时坐标系也发生改变;χ1、χ2为ALE坐标系,ALE坐标系不固定在任何一个位置,坐标网格可以按照一定规律进行运动,这是ALE坐标系的优点[4]。
ALE坐标系下网格位移、网格速度的定义:
在ALE方法中,通过控制网格的移动速度v^来实现网格的移动和更新。
2 算例验证与分析
2.1 自适应网格优化验证
采用NACA0012非结构计算网格,计算工况如表1所示,对初始网格根据流场结果进行基于马赫数的自适应。图3是在给定计算工况下的流场马赫数云图。
图4是误差密度分别为0.1和0.01的对称面自适应网格比较图。可以看到,在对流场网格采用了基于马赫数的网格自适应方法后,网格自动在马赫数梯度较大的地方进行了加密,整个网格较初始网格明显致密。误差密度越小,网格在马赫数梯度较大的地方越致密,精度也就越高。
2.2 ALE网格重构法验证
针对积冰模型,把模拟积冰总时长分为若干步,每当计算完当前时间步积冰外形后,利用ALE方法对网格进行重构,从而对冰层增长进行追踪,得到积冰后的重构网格,然后再次进行流场计算→水滴撞击计算→冰层增长计算的循环操作,直到达到模拟积冰的总时长。本节采用NACA0012结构网格,表2列出了Case2的计算工况,计算结果如图5到7所示。
比较图5和图6可以看出单步法进行积冰计算时,把积冰看作是定常稳态的过程,随着积冰时间的增长,冰形變化不大;而对比图5与图7可以明显的观察到,冰形已经发生了变化,随着时间的推移,前缘逐渐形成了冰角,这是因为采用时间多步法时等于考虑了积冰过程的非稳态效应,将积冰时间2.5min分为两个时间步,在进行1.5min积冰后采用ALE方法对积冰网格进行重构,再次进行流场计算→水滴撞击计算→冰层1min增长计算,对比参考文献[5]可知,基于ALE网格重构的多步法计算更为准确,能够较好地模拟积冰增长。
3 结语
本文研究并提出了一种可以提升积冰模拟精度的方法,采用基于ALE网格重构的多步法进行冰层增长计算,一个时间步内的计算流程为:网格自适应流场计算——水滴撞击特性计算——冰层增长计算——ALE网格重构,有利于提高积冰模拟的精度,使得仿真结果更加接近于实验数据。最后通过算例验证了这种方法计算出的冰形更加接近实验冰形,具有一定的可靠度。
参考文献:
[1]J.Dompierre,M-G.Vallet,Y.Bourgault,M.Fortin and W.G.Habashi,Anisotropic Mesh Adaptation:Towards User-Independent,Mesh-Independent and Solver-Independent CFD Solutions:Part Ⅲ:Unstructured Meshes,International Journal for Numerical Methods in Fluids,Vol.39,pp.675-702,June 2002.
[2]NTI.FENSAP-ICE User Manual[M].Canada H3A 2M7.2007:117-138.
[3]江召兵,沈庆,等.ALE动网格法在流固耦合数值模拟中的应用[J].应用力学学报,2008,25(4):669-672.
[4]王学.基于ALE方法求解流固耦合问题[D].湖南:国防科学技术大学,2006.
[5]WB.Wright,A.Rutkowski.Validation Results for LEWICE 2.0[R].NASA/CR-1999-208690,1999.
作者简介:胡义明(1995—?),男,汉族,江西南昌人,硕士,助理工程师,主要研究方向:无人机系统总体设计、飞机防除冰技术。

