基于UGNX求作两曲面立体相贯线的投影分析
谭玉华

摘要:运用UG NX三维模型实现了辅助球面法及辅助柱面法求相贯线过程的演示,相贯线的提取及定向图为作相贯线投影图提供准确依据,并通过调节模型中辅助面的透明度,展示并剖析了两种方法求作复杂曲面立体相贯线的投影过程和三面共点原理,从而使复杂曲面立体相交的情况变得简单明了。
关键词:相贯线; 三面共点原理; 辅助面; UG NX应用
中图分类号:TH126 文献标识码:Adoi:10.14031/j.cnki.njwx.2016.10.005
Abstract: In this paper, UG NX three-dimensional model to be used, implements the auxiliary spherical method and auxiliary cylindrical curve method in the process of demonstration, interfingering lines to be extracted and directional provide accurate data projection, and assist the transparency, by adjusting the model and analyze the two kinds of methods for seeking the complex curve surface stereo projection process and principle of phase line three sides of concurrent so that three-dimensional intersection shall be more simple and clear.
Keyword: Interfingering line; Principle of phase line three sides of concurrent; auxiliary plane; UG NX applications.
0 引言
在画法几何学课程中,两曲面立体相贯的交线即相贯线的投影部分是较难理解的内容之一,其求作的常用方法有积聚性法、辅助平面法、辅助球面法、辅助柱面法等[1-3]。前两种方法相对简单,但要受到许多条件的限制。
(1)相贯线在两个投影面上有积聚性时,可以直接用表面取点方法求作。
(2)相贯线只在一个投影面上有积聚性或在三个投影面上都没有积聚性可利用时,就要用到辅助平面法求作,但此时所用到的辅助平面必须是有利于解题,但辅助球面、辅助柱面法这两种方法则要求相贯体之间及其对投影面有特殊位置关系,无论采用何种方法求贯线都是利用三面共点原理进行求作。
积聚性法与辅助平面法较为简单,本文只着重对后两种方法如何运用UGNX软件进行相贯线的求解过程及其投影进行分析。
1 辅助球面法
当两回转体轴线斜交时不宜采用辅助平面法求作相贯线,而通常采用的是以球面作为辅助面进行求作相贯线的投影。辅助球面法分为定心球面法和变心球面法。本文将以圆柱与回转体轴线斜交、圆台与圆环相交为例,首先运用UG软件创建出两个相交的回转体模型,运用[求交]命令求出相贯线,再利用[移动对象]命令将相贯线线移出相贯体外,从而可看到移出后的相贯线空间几何形状,通过[定向视图]命令来进一步观察相贯线在V、H、W投影面上的投影形状[4],为相贯线的二维作图提供准确依据。同时运用UG软件来分析定心球面法和变心球面法求作相贯线的过程,同时在三维模型中通过改变辅助球的透明度来观察相贯线上一系列共有点的位置及求作过程。
1.1 定心球面法
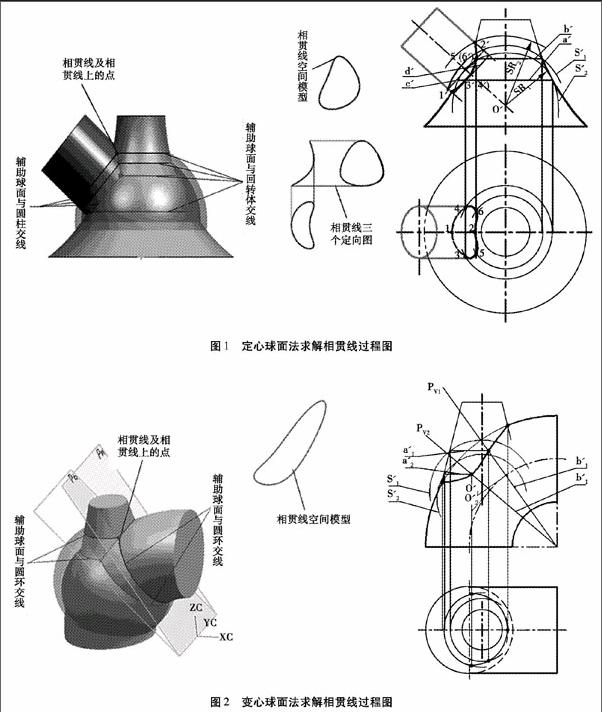
定心球面法是以两回转体轴线交点为辅助球的球心,以不同半径的球面为辅助面,同时与两回转体相交,得到两交线的交点即为相贯线上的点。如图2所示,特殊点1′和2′可直接获得,对于一般位置点可在最大SR2和最小SR1两个极限半径内作多个辅助球,如图中S1、S2两个辅助球,与两回转体交线的正面投影分别为a′和d′之交点3′(4′)、b′和c′之交点5′(6′),按此方法即可得到相贯线上的若干点,光滑连线即获得所求相贯线的投影。图1为相交的两曲面立体及所有辅助球面与之交线及相贯线的三维模型及投影作图过程。
1.2 变心球面法
当两相交的回转体轴线不相交,用辅助平面法和定心法球面法求解相贯线的条件都不充分时,可用变心球面法求作其相贯线的投影(变心球面法介绍的很少)。变心球面法是用改变辅助球心的位置和半径作出不同的辅助球面来获得一系列相贯线上点的投影,如图2所示。
在图2投影图中,通过圆环轴线作多个正垂面,这里只作了两个正垂面PV1与PV2,该正垂面与圆环的交线为一圆,若作一辅助球面,要求同时与锥面和环面交线都为圆,那么球心必定在过该圆(球面与环面交线圆)并垂直于圆平面的垂线与圆锥轴线的交点上(图2中O′1和O′2)。分别以O′1和O′2为球心作球面S1、S2获交线圆a′1、a′2、b′1、b′2,a′1与b′1、a′2与b′2之交点即为相贯线上的点,求作过程如图2所示。
在三维模型中,各型体赋予不同颜色,并通过调整辅助球面的透明度及三维模型仿真以观察相贯线的求解过程,使得难以理解的变心球面法变得直观、易懂。
2 辅助柱面法
当两相交的回转体轴线相交,如斜椭圆柱与抛物回转体相交,如图3所示。虽然两回转体轴线相交,但无法用平面及球面作辅助面求其相贯线,对于特殊点V、VI可直接获得,一般位置点可通过辅助柱面法求解。在椭圆回转体轴线上取系列点,如图3中O1′、O2′,并以其点为圆心在V、VI之间作水平圆(a′、a;b′、b),再以此圆为底作平行于已知斜椭圆柱的辅助圆柱A和B,得到交线A1、A2和B1、B2的交点I、II和III、IV,按投影关系完成其余各点投影,光滑连接得到相贯线的投影,求作过程如图3所示。
3 结束语
通过UG NX三维软件实现了对辅助球面法及辅助柱面法求作贯线原理及过程仿真的演示,并通过调节辅助面的透明度来观看相贯线上系列点的获得及求作过程,展示了利用“三面共点”原理求相贯线所具有的直观性和独特的优势,UG NX与画法几何的有机结合使得复杂曲面回转体相交的情况变得简单明了,同时也为较少介绍的辅助球面法和柱面法的求解提供了一些方法和借鉴。
参考文献:
[1]大连理工大学工程图学教研室编. 画法几何学[M]. 北京:高等教育出版社,2011.
[2]张大庆,田风奇,赵红英,等.画法几何基础与机械制图[M]. 北京:清华大学出版社,2012.
[3]合肥工业大学工程图研究室. 画法几何学[M]. 北京:机械工业出版社,1999.
[4]展迪优. UG NX7.0曲面设计教程[M]. 北京:机械工业出版社,2012.


摘要:运用UG NX三维模型实现了辅助球面法及辅助柱面法求相贯线过程的演示,相贯线的提取及定向图为作相贯线投影图提供准确依据,并通过调节模型中辅助面的透明度,展示并剖析了两种方法求作复杂曲面立体相贯线的投影过程和三面共点原理,从而使复杂曲面立体相交的情况变得简单明了。
关键词:相贯线; 三面共点原理; 辅助面; UG NX应用
中图分类号:TH126 文献标识码:Adoi:10.14031/j.cnki.njwx.2016.10.005
Abstract: In this paper, UG NX three-dimensional model to be used, implements the auxiliary spherical method and auxiliary cylindrical curve method in the process of demonstration, interfingering lines to be extracted and directional provide accurate data projection, and assist the transparency, by adjusting the model and analyze the two kinds of methods for seeking the complex curve surface stereo projection process and principle of phase line three sides of concurrent so that three-dimensional intersection shall be more simple and clear.
Keyword: Interfingering line; Principle of phase line three sides of concurrent; auxiliary plane; UG NX applications.
0 引言
在画法几何学课程中,两曲面立体相贯的交线即相贯线的投影部分是较难理解的内容之一,其求作的常用方法有积聚性法、辅助平面法、辅助球面法、辅助柱面法等[1-3]。前两种方法相对简单,但要受到许多条件的限制。
(1)相贯线在两个投影面上有积聚性时,可以直接用表面取点方法求作。
(2)相贯线只在一个投影面上有积聚性或在三个投影面上都没有积聚性可利用时,就要用到辅助平面法求作,但此时所用到的辅助平面必须是有利于解题,但辅助球面、辅助柱面法这两种方法则要求相贯体之间及其对投影面有特殊位置关系,无论采用何种方法求贯线都是利用三面共点原理进行求作。
积聚性法与辅助平面法较为简单,本文只着重对后两种方法如何运用UGNX软件进行相贯线的求解过程及其投影进行分析。
1 辅助球面法
当两回转体轴线斜交时不宜采用辅助平面法求作相贯线,而通常采用的是以球面作为辅助面进行求作相贯线的投影。辅助球面法分为定心球面法和变心球面法。本文将以圆柱与回转体轴线斜交、圆台与圆环相交为例,首先运用UG软件创建出两个相交的回转体模型,运用[求交]命令求出相贯线,再利用[移动对象]命令将相贯线线移出相贯体外,从而可看到移出后的相贯线空间几何形状,通过[定向视图]命令来进一步观察相贯线在V、H、W投影面上的投影形状[4],为相贯线的二维作图提供准确依据。同时运用UG软件来分析定心球面法和变心球面法求作相贯线的过程,同时在三维模型中通过改变辅助球的透明度来观察相贯线上一系列共有点的位置及求作过程。
1.1 定心球面法
定心球面法是以两回转体轴线交点为辅助球的球心,以不同半径的球面为辅助面,同时与两回转体相交,得到两交线的交点即为相贯线上的点。如图2所示,特殊点1′和2′可直接获得,对于一般位置点可在最大SR2和最小SR1两个极限半径内作多个辅助球,如图中S1、S2两个辅助球,与两回转体交线的正面投影分别为a′和d′之交点3′(4′)、b′和c′之交点5′(6′),按此方法即可得到相贯线上的若干点,光滑连线即获得所求相贯线的投影。图1为相交的两曲面立体及所有辅助球面与之交线及相贯线的三维模型及投影作图过程。
1.2 变心球面法
当两相交的回转体轴线不相交,用辅助平面法和定心法球面法求解相贯线的条件都不充分时,可用变心球面法求作其相贯线的投影(变心球面法介绍的很少)。变心球面法是用改变辅助球心的位置和半径作出不同的辅助球面来获得一系列相贯线上点的投影,如图2所示。
在图2投影图中,通过圆环轴线作多个正垂面,这里只作了两个正垂面PV1与PV2,该正垂面与圆环的交线为一圆,若作一辅助球面,要求同时与锥面和环面交线都为圆,那么球心必定在过该圆(球面与环面交线圆)并垂直于圆平面的垂线与圆锥轴线的交点上(图2中O′1和O′2)。分别以O′1和O′2为球心作球面S1、S2获交线圆a′1、a′2、b′1、b′2,a′1与b′1、a′2与b′2之交点即为相贯线上的点,求作过程如图2所示。
在三维模型中,各型体赋予不同颜色,并通过调整辅助球面的透明度及三维模型仿真以观察相贯线的求解过程,使得难以理解的变心球面法变得直观、易懂。
2 辅助柱面法
当两相交的回转体轴线相交,如斜椭圆柱与抛物回转体相交,如图3所示。虽然两回转体轴线相交,但无法用平面及球面作辅助面求其相贯线,对于特殊点V、VI可直接获得,一般位置点可通过辅助柱面法求解。在椭圆回转体轴线上取系列点,如图3中O1′、O2′,并以其点为圆心在V、VI之间作水平圆(a′、a;b′、b),再以此圆为底作平行于已知斜椭圆柱的辅助圆柱A和B,得到交线A1、A2和B1、B2的交点I、II和III、IV,按投影关系完成其余各点投影,光滑连接得到相贯线的投影,求作过程如图3所示。
3 结束语
通过UG NX三维软件实现了对辅助球面法及辅助柱面法求作贯线原理及过程仿真的演示,并通过调节辅助面的透明度来观看相贯线上系列点的获得及求作过程,展示了利用“三面共点”原理求相贯线所具有的直观性和独特的优势,UG NX与画法几何的有机结合使得复杂曲面回转体相交的情况变得简单明了,同时也为较少介绍的辅助球面法和柱面法的求解提供了一些方法和借鉴。
参考文献:
[1]大连理工大学工程图学教研室编. 画法几何学[M]. 北京:高等教育出版社,2011.
[2]张大庆,田风奇,赵红英,等.画法几何基础与机械制图[M]. 北京:清华大学出版社,2012.
[3]合肥工业大学工程图研究室. 画法几何学[M]. 北京:机械工业出版社,1999.
[4]展迪优. UG NX7.0曲面设计教程[M]. 北京:机械工业出版社,2012.

