核心素养理念下的初中数学深度教学实践

    杭霞

    

    [摘? 要] 随着新课改理念的深入，初中数学核心素养教学进入一个新的阶段. 教師基于核心素养授课，如何落实核心素养教学理念就成为当前亟待解决的问题. 鉴于此，文章就核心素养理念下的初中数学深度教学展开研究.

    [关键词] 核心素养;初中数学;深度教学

    相较于接受式传统教学，深度教学能促进学生对数学学科的深入思考，能加深学生对所学内容的理解，从而生成数学思维. 可以说，深度教学是当前课堂教学改革纵深推进的方向. 在笔者看来，深度教学不能刻意追求教学内容本身的深度和难度，而是要相对于学科内容的构成要素来追求内容的全面，以及深层次的理解.

    ■ 核心素养理念下深度教学的价值

    纵观新课改，数学教师开展了多种教学模式，如小组合作、分层教学、有效课堂，看似教学氛围热闹、师生互动频繁，充满生机与活力，但细究之后会发现，少部分数学教学游离于学科知识与本质之外，对教学内容理解的深度不够，学生的数学思维表面化，缺乏对数学知识的深度思考，更不要说培养核心素养了.

    核心素养理念下的深度教学成为解决上述问题的突破口. 教师在深刻理解教材教学思想基础上启发学生智慧，发展个体数学思维，把课堂变成师生深度对话与交流的场所. 从某种意义上来讲，转知成慧是深度教学的目的，这就要求教学一方面要重视知识系统性，另一方面要站在智慧角度来把握数学教学内容，以“建构知识，提升能力，培养素养”为教学目标. 在笔者看来，深度教学具有以下两点优势：（1）让学生有独立、长时间的思考，使他们在思考过程中发展自身数学思维，提升对知识的理解深度;（2）让课堂有积极、深刻的深度对话. 对话是课堂教学的基本形式，学生在深度对话中经历对知识的层层深入，通过抽丝剥茧般地探究问题来掌握本质，借助对话形成数学语言逻辑性、缜密性，养成良好的情感、态度与价值观，而这也是数学教育的价值追求.

    ■ 核心素养理念下初中数学深度

    教学策略

    开展初中数学深度教学，要围绕培养初中生数学学科核心素养这一要求，探求“深度的教”与“深度的学”相结合，探讨学科本质，促进对知识的自主发现和真正理解.

    1. 基于学科本质，推进深度教学

    从数学学科角度看，深度教学要能体现和反映学科本质. 张奠宙先生认为，“数学本质”的内涵为：数学知识的内在联系;规律的形成过程;思想方法的提炼;理性精神的体验. 在深度教学中，教师要让学生深入理解数学概念、原理及知识的发生、发展过程，挖掘内在的数学思想，使他们不但知其然，而且要知其所以然. 在数学教学过程中，问题串能引导学生进行深度思考，能带领学生通过步步探究掌握知识，完善数学认知结构，发展思维能力.

    例如，讲解“有理数的加法与减法”时，可以通过问题串来进行教学.

    问题1：对于有理数的加法法则，同号两数相加、异号两数相加、一个数和0相加，分别为______.

    问题2：有理数的减法法则，减去一个数等于加上这个数的______.

    问题3：有理数加减混合运算的步骤是什么？

    仔细分析，这一教学设计层次性较强，能引导学生步步深入地探究问题的答案，能促使学生正确掌握有理数加、减运算法则及加减混合运算，能解决生活中的简单问题，能有效提升运算准确性. 在学习过程中，班级学生在理解理论知识后进行课堂练习活动，体会和感受到了数学与生活的紧密联系，形成了运用运算解决生活问题的能力. 通过课堂教学，学生初步体会了化归思想、数形结合思想与分类讨论思想，在师生互动中形成了比较和概括的思维能力. 在整个教学过程中，教师培养学生严谨地看待数学问题，以层层递进的方式来展开探索，形成坚韧、执着的态度，这也是数学教学践行立德树人、培养核心素养所需的宝贵财富.

    2. 聚焦主题教学，促进深度理解

    众所周知，学生纵向（深度）学习要比横向（广度）学习难度大得多，那么，如何引导他们体会和掌握知识间的纵向联系，促进其对数学知识的深刻理解，就有待做深入思考. 而主题式教学恰恰可以实现知识间的纵向联系. 基于核心素养理念的主题教学，教师要从一节一节的课程中跳出来，从整体视角来看数学章节，选择教材中某一个或某几个“主题”作为思考对象. 开展主题教学前，初中数学教师要设计好整体计划，以学生的深度学习为目标来进行设计，这也是整体提升初中数学课程质量的关键. 实际上，主题教学更加符合学生螺旋式上升的认知规律，能使他们不断地在“现有发展区”和“最近发展区”之间循环，不断通过实现知识迁移来发展数学思维能力.

    以“勾股定理的应用”为例，笔者要教会学生把实际问题转化为直角三角形数学模型，用勾股定理来解决，并充分渗透数形结合思想. 上课后，学生先回忆勾股定理的数学表达式，根据给出的图形，运用勾股定理求解各边的长. 紧接着，通过生活中的数学试题，使他们进一步体会到勾股定理在生活中的广泛应用，提升实际解题能力. 在学生初步具备解题能力后，教师通过设计最短路径问题来进行深入探究，即，以“将军饮马问题”“直线外一点与直线上一点的连线中垂线段最短”来设计两道试题，以此提升教学深度. 此外，在勾股定理的应用教学中，教师不妨结合现代科学技术来设计试题，注重应用的广泛性，使学生认识到勾股定理解决问题的有效性. 借助深度教学，教师可以帮助学生对知识的认知实现螺旋式上升.

    3. 倡导问题导向，鼓励深度思考

    问题是数学课堂教学的精髓，也是学生思维的引擎. 借助问题开展数学课堂教学，有助于引导学生的思维向更深层次发展. 在数学课堂中，问题的来源有两个方面：一是教师借助教学参考书和深挖教材所得;二是学生在课堂中通过互动提出有价值的问题. 问题是对知识的思考和探究，长期以来，数学课堂教学忽视了对思考和探究能力的培养，无法在教学中发散学生的数学思维，导致学生独立探究知识能力很差. 基于此，数学教师要鼓励学生在学习中敢于对知识进行质疑，鼓励学生通过一题多解和变式训练来提出自己的看法，唯有如此，才能在问题导向下发展数学核心素养.

    例如，在初三数学的学习过程中，笔者曾经出过这样一道试题：在△ABC中，AB边上的中线CD=■AB，证明：△ABC是直角三角形.

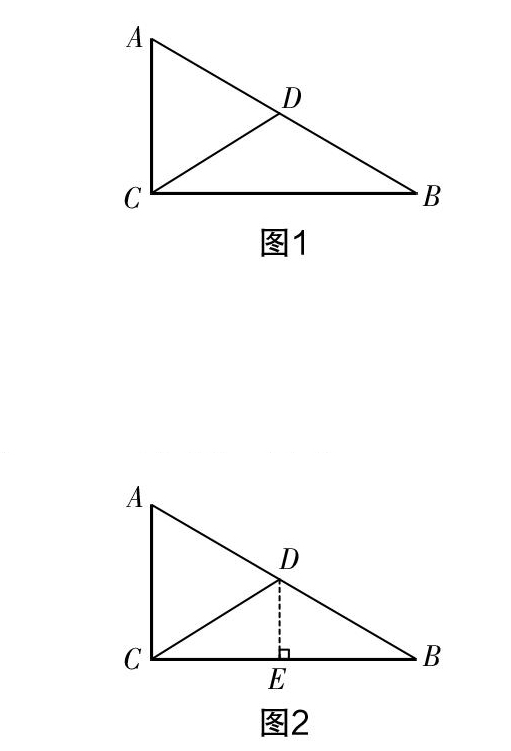
    解法1：如图1，由CD=BD，AD=CD，得到∠A=∠ACD，∠DCB=∠B. 又∠A+∠ACD+∠DCB+∠B=180°，所以∠A+∠B=∠ACB=90°. 所以△ABC是直角三角形.

    解法2：如图2，过点D作DE⊥BC，交BC于点E，由△BDE和△BAC相似来得到△ABC为直角三角形.

    实际上，本题的解决方法还有很多种. 在练习的过程中，学生会积极地与小伙伴进行讨论，找到试题背后的多种解法，形成正确的数学思维，提升解题能力. 在一题多解训练过程中，学生以问题为导向展开研究和讨论，提出自身的看法，有效地发展了数学解题能力.

    又如，讲解完完全平方公式之后，学生要对（a±b）2展开为三项二次式，他们虽然能初步理解所学知识，但并不代表能完全掌握完全平方公式. 于是，笔者布置了以下几道试题：（a+______）2=a2+6ab+______;（2a-______）2=______-4ab+b2;（______+2y）2=______+12xy+______;（______+y）2=16x2+______+y2. 完成上述填空，不仅能深化学生对完全平方公式的理解，还能锻炼他们的逆向思维能力. 等学生熟练运用完全平方公式之后，再提出变形：已知（a-b）2=21，a2+b2=10，求ab的值;已知（a+b）2=8，ab=3，求a2+b2的值;已知（a+b）2=13，ab=7，求（a-b）2的值.

    作为开展深度教学的主体，教师要想在课堂授课时做到“游刃有余”，就必须深入研究与本节教学内容相关的素材，注重把握教学的“度”与学生的“悟”之间的关系，不能为了教学深度而随意拔高教学内容的“难度”，而是要让学生“跳一跳”后摘到“桃子”. 当然，核心素养导向下的深度教学的目的是促进学生深度学习，所以教师要积极展开创新实践，发展学生的数学核心素养，从而实现初中数学课程的价值追求.