巧借课后习题 助力课堂教学
卢春华

[摘? 要] 课后习题具有巩固所学知识、开发学生思维等作用. 但在实践中,部分教师常忽略课后习题的重要性,表现出对待课后习题过于随意,缺乏关注,不能发挥课后习题的有效价值等弊端. 文章从课后习题对教学思路、概念学习、问题发生与逻辑思维等方面的影响出发,浅析课后习题对初中数学课堂教学的作用.
[关键词] 课后习题;课堂教学;概念;解题
教材中的课后习题是编者综合教学大纲、课程标准与学生的认知水平等精心编拟而成的,是数学教学中不可或缺的重要组成部分之一,亦是一线教师制定教学目标的可靠依据. 但在教学实践中,不少教师没有充分认识到课后习题的重要性,从而忽视了课后习题的导向作用,让它成为教学过程中的一个摆设. 若教师能将课后习题融合到课堂教学的每一个环节,落实到概念、解题以及学生思维成长等方面,那它将起到巩固所学内容、提高学生认知水平、拔高思维、提升数学核心素养的重要作用.
关注课后习题,明晰教学思路
初中数学教材的每个单元都设有配套的课后习题,这些习题不但具有考查和巩固学生的学习情况的作用,还具有为教师的教学指明方向、突出教学重点与难点的作用. 课后习题反映的是编者对教材内容的解释和暗示,也是教材与教师的一种特殊对话模式. 经过编者精心设计的课后习题,一般是从教学重点与难点入手,以典型习题的形式呈现. 教师在备课时若能抓住课后习题,就是抓住了教学的命脉,明确了课堂教学的目标. 因此,充分发挥课后习题对教学的导向作用,能为教师的教学设计明晰思路.
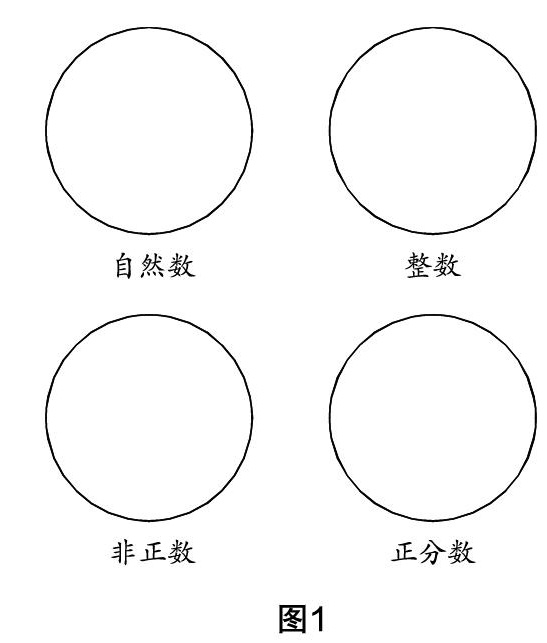
例1?将下列各数填写到相应的圈(图1)中:
-1,8,-0.03,■,-43,0,-1■,5.■,9%,13.
教师可借助本题来明晰本章节的教学重点与难点,根据不同标准对有理数进行分类处理. 因此,教学设计时可按照整数和分数来分,再按正负来分,由此理清整个教学思路(如图2).
依托课后习题,夯实概念基础
当前,不少教师认为概念只是寥寥几行文字,读读背背就行了,不需要作为教学的重点,这种现象是教学的重大误区. 事实上,概念是学习的基础与前提,不理解概念的学习是徒劳的,解决问题时会因概念模糊而出现各种错误. 而课后习题是夯实概念教学的利器,教师通过教学活动的开展进行概念教学,再依托课后习题进行训练,能有效地提高概念的教学效果.
例2?-2的绝对值是______,绝对值是2的数有________,0的绝对值是________.
“有理数”章节的知识点比较零碎,尤其是绝对值部分,学生在概念掌握上总觉得力不从心. 此时教师可利用课后习题来巩固各个概念,而不是强制学生机械地诵读.
-2的绝对值是2,0的绝对值是0,学生很容易理解;绝对值是2的数则出现了两种情况,这就要求学生对绝对值的概念要理解透彻:所谓绝对值,是指数轴上的一个数,其对应点到原点的距离,常用“”来表示,如2的绝对值为2,-2的绝对值也是2.
教师可通过上述习题进行知识的拓展与延伸. 如问学生:在有理数-1, 1,0中,绝对值最小的是谁?如果x=x,则-x一定是正数、负数或非正数、非负数吗?学生经过思考与探索后会得到如下结论:正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数,即a=a(a>0),0(a=0),-a(a<0).
本题看似简单,却考查了学生对绝对值的掌握情况. 教师不能只关注学生填空的结果,而忽视本题对概念教学的价值,应抓住此题的关键点,紧扣绝对值的概念,让学生从习题中获得基本概念,巩固概念内容,这樣才能真正把握概念的内涵,为接下来的学习夯实基础.
借助课后习题,提升解题能力
目前,不少教师将教学的重心放在问题的“巧解”中,而忽略了常规题目的解题过程. 当然,能巧妙地使用便捷的方法解决问题,既省时省力,正确率又高,有事半功倍之功效,但使用便捷的方法解决问题并不具有普遍性,而使用常规方法解决问题才是数学学习的根本. 因此,教师应借助课后习题,发展学生的常规解题能力.
例3?在Rt△ABC中,∠C=90°,BC=12,AC=24,求AB.
不少学生看到此题,直接使用简化计算方法:将BC的值看作1,将AC的值看作2(同时除以12),先计算出直角边为1和2的直角三角形的斜边的值,再用所求的斜边的值乘12,获得最终的结论. 但是,这种简化计算方法并不适用于所有勾股定理的习题,只有运用a2+b2=c2进行计算,才是解决此类问题的关键,这也要求学生要掌握数字的乘方、开方计算方法.
相较于便捷的“巧解”方法,常规方法费时费力,特别是数据复杂的情况下,还容易出现运算错误. 但是,常规解题办法却是永不过时的解题武器,学生只有熟练掌握常规方法后,才能根据习题特征,酌情使用巧解方法. 想要真正地掌握解题思想,只有踏踏实实地在常规解题中不断地重复训练,才能有所收获.
巧用课后习题,暴露常规错误
在教与学的过程中,师生常常会产生一个困惑:授课内容已经听懂了,但是解题时却出现思维卡壳,找不到解题思路或出现解题错误的情况. 究其原因,主要在于教师过于追求教学效率,教学中不自觉地为学生创建了一些思维捷径,以便学生更快更好地掌握知识点. 而事实却是事与愿违,学生缺乏自主探索的过程,难以做到知其然,且知其所以然,存在的问题也就在解题过程中得以暴露.
例4?电动车以30 km/h的速度往正北方向行驶,于A处看到路灯O在电动车北偏东30°方向上,电动车行驶2 h后到达B处,看到路灯O在电动车的北偏东45°方向上. 请求出路灯O到B的距离.
在“锐角三角函数”的内容已经学完的基础上,常会出现如例4与生活实际相关的应用类问题,其中最常见的是运动类问题,学生在解题中常会暴露各种错误. 解决本题时,学生暴露的问题主要是不知道用什么基准来确定图像. 此问题形成的主要因素是,教师在执教时,直接将图像呈现给学生,学生没有经历图像形成的过程,缺乏探索与思考,导致遇到实际问题时感到茫然而无从下手.
由于课堂时间与空间的局限,导致教师无法在有限的时间内发现教学中存在的漏洞与问题,而课后习题却具有查漏补缺的功能. 解题需要学生依靠自主分析与思考独立处理问题,学习中存在的问题也随着解题而暴露. 因此,教师应关注学生的解题过程,及时发现学生学习中存在的漏洞与错误,根据实际情况因势利导地调整教学方法,查漏补缺,帮助学生完善知识结构.
妙用课后习题,培养逻辑思维
教师在课堂教学过程中常存在一个误区,那就是对学生的逻辑思维能力掌握得不准确,导致学生跟不上授课进度,进而出现思维被“拖着跑”的现象. 其原因是教师对知识掌握的熟练程度明显优于学生,教师授课时能根据具体情况迅速做出正确的判断与思考,而学生处在摸索阶段,思维还没反应过来,教师已进入新的教学环节. 此过程,教师最大的误区就是忽视了学生的逻辑思维能力水平. 因此,教师可利用课后习题的作用,充分培养学生的思维能力,让学生在解题过程中逐渐获得数学思想.
例5?解方程:■-■=1.
“平方根里面的数不小于0”是学生熟记于心的概念,部分教师理所当然地认为解二次根式类的方程,代入验根是必然的. 但是,不少学生在解这个方程时,却得到了x1=2,x2=7的结论. 若将结论代入原题检验,就会发现错误所在,但不少学生却省略了这一步骤. 这出乎教师的意料. 而从学生的角度来看,只要解出方程,任务就完成了,至于代入验根这一步却忘到九霄云外了. 这就要求教师要站在学生的角度,观察学生的思维走向,并及时引导与纠正,将学生带到学习的正轨中. 鉴于此,教师在教学中要因材施教地调整教学方法,重点强调一些容易被学生忽视的细节,以促进学生逻辑思维能力的发展.
总之,教师在教学过程中存在的一些误区,可通过课后习题的训练,达到明晰教学思路、提高学生解题能力、查漏补缺、提升学生逻辑思维能力的作用. 同时,教师应明确课后习题对教学的指向性,关注学生的解题方法与思维过程,实现以课后习题助力初中数学课堂教学的目标.

