建构知识体系 落实核心素养
刘兴安
[摘? 要] 以二次函数复习教学为例,根据新课程标准的要求,大胆设计教学内容,有效组织实施教学过程,取得了良好的教学预期,有效实现了学生知识体系的构建,以及核心素养的生成.
[关键词] 二次函数;复习课;核心素养
九年级的数学复习课,不能就是讲几道典型例题了事,而应厘清数学对象的基本思路与方法,勾起学生回忆,让学生重构知识体系,通过一系列有序的问题提升学生的思维水平,通过典型例题的解读提高学生分析问题、解决问题的能力;同时,在各个环节不断渗透数学基本思想方法,全面落实核心素养. 笔者在前不久执教了一节数学复习课,课题为“二次函数”,根据新课程标准的要求,大胆设计教学内容,有效组织实施教学过程,赢得了一致好评. 现将本节课作一呈现,以供点评.
学情分析
本节课所授班级的学生数学基础知识扎实,知识接受能力强,普遍成绩比较好.二次函数的相关知识学生在新知学习时已经掌握,能够用二次函数的模型解决具体的实际问题,对于函数的学习积累了一些基本方法与经验,学生有一定的观察能力、总结概括能力,知道数形结合、分类讨论、特殊与一般等数学思想.但学生的思维还是以形象思维为主,处于由形象思维向抽象思维过渡的阶段.
复习目标
(1)掌握二次函数:形式、图像与性质,学会运用不同的方法确定二次函数解析式;理解二次函数、一元二次方程、一元二次不等式三者的相互联系.
(2)亲历二次函数相关知识的梳理过程,进一步熟悉研究函数的基本思路与方法,提升观察图形、分析图形的能力,体会数形结合等数学思想.
(3)体验数学知识之间的相互联系,学会从生活化问题中抽象函数模型,并应用其解决生活问题,使数学抽象与数学建模的核心素养落地生根.
教学呈现
1. 温故知新,知识再构
师:二次函数是我们九年级学习的一类函数,关于二次函数我们学习了哪些内容?这些内容又是如何学习得到的?
生:二次函数我们学习了它的概念、图像与性质;二次函数与一元二次方程、一元二次不等式的相互关系;二次函数在实际生活中的应用;二次函数图像与几何图形的综合;等等.
生:二次函数的研究是这样的:由实际生活的事例,提取二次函数模型;由二次函数的表达式用描点法画出二次函数的图像;由二次函数的图像来研究二次函数的性质,在研究二次函数的性质时,按从特殊到一般的规律进行研究;然后探究二次函数与一元二次方程、一元二次不等式之间的联系,最后应用二次函数的性质解决实际问题.
师:在学习二次函数的过程中,我们学习了哪些数学思想与方法?
生:待定系数法、配方法、数形结合思想、从特殊到一般的思想、方程思想、函数思想.
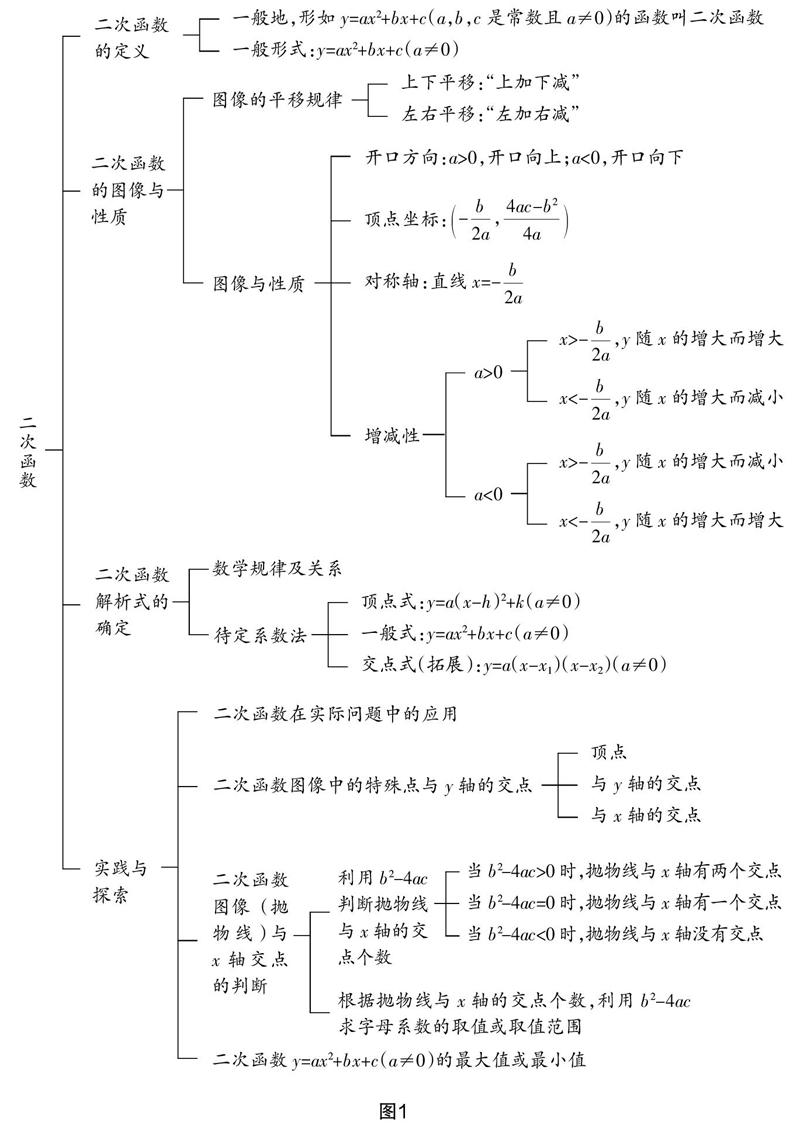
师:请同学们用自己的方式表示二次函数所有知识点之间的纵横关系.
经过15分钟的讨论、争论,师生共同总结的内容如图1.
设计意图? 在复习前,在学生头脑中二次函数的知识是孤立的、分散的,所以,复习中,教师应引导学生再建知识结构图,理清二次函数相关知识的发生、发展脉络,掌握二次函数的核心知识与研究函数的一般方法,不仅要通过文字语言表述二次函数的相关内容,而且要与图形语言、符合语言相互配合与转化,加深学生对数学语言的理解与掌握,从而提高学生对二次函数性质、相关思想方法的理解与认识.
2. 数形联手,构建联系
师:画二次函数y=ax2+bx+c(a≠0)的图像的一般步骤是什么?
生:画二次函数y=ax2+bx+c(a≠0)的图像的一般步骤是:(1)先将二次函数的表达式配方成y=a(x-h)2+k(a≠0)的形式,找出抛物线的开口方向、对称轴及顶点坐标;(2)以对称轴为中心列表;(3)描点,连线.
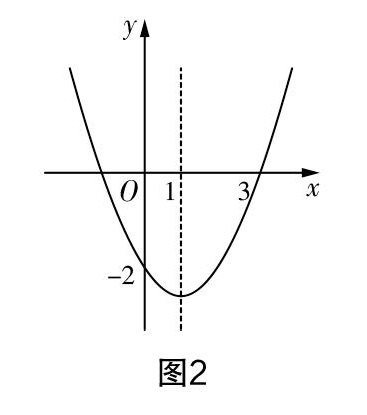
师:如果二次函数y=ax2+bx+c(a≠0)的图像如图2所示,观察函数图像,你能从中得到什么信息呢?
生:抛物线的对称轴为直线x=1,与y轴的交点坐标为(0,-2),根据抛物线的对称性,得到抛物线与x轴的两个交点的坐标为(-1,0),(3,0).
生:当x<-1或x>3时,y>0;当x=-1或3时,y=0;当-1 生:根据抛物线与坐标轴的三个交点坐标,可求得抛物线的解析式为y=■x2-■x-2,顶点坐标为1,-■. 生:一元二次方程■x2-■x-2=0有两个不相等的实数根,一元二次方程■x2-■x-2=-■有两个相等的实数根. 师:如图3,如果增加直线y=-■x,观察图像,你又能得到什么样的结论? 生:联立得方程组y=■x2-■x-2,y=-■x,解得x■=-2,y■=■;x■=■,y■=-■.说明直线与抛物线的交点坐标为-2,■,■,-■. 师:根据图像信息,可以求出函数解析式、方程的解或方程组的解,可以得到不等式的解集,那么同学们能从中得到不等式组的解集吗? 生:不等式组■x2-■x-2>0,-■x>0 的解集是x<-1;不等式组■x2-■x-2>0,-■x<0 的解集是x>3. 设计意图? 函数解析式反映了函数中两个变量之间的数量关系,而函数图像则是用图形反映了两个变量之间的变化趋势,函数解析式精确不直观,函数图像直观不精确,当两者结合时,就能发挥两者的优势,通过观察函数图像,利用函数图像与坐标轴的交点坐标,两个函数图像的交点坐标等特殊点的坐标,学生发现了诸多有用的结论,从而将二次函数、二次方程、二次不等式三个二次有机结合在一起,加强了三者之间的沟通与比较. 3. 应用模型,回归生活 数学知识抽象于生活,同时又服务于生活,通过数学模型建构解决生活中的实际问题,是落实核心素养的有效举措,对促进学生的核心素养生成具有重要作用. 例如,大华超市在销售一种商品时发现,商品每月卖出的数量是销售单价的一次函数,其中某种商品的销售单价与月销售量之间有如下的对应关系. 注:月销售利润=月销售量×(售价-进价). (1)①求y关于x的函数表达式; ②当该商品的售价是多少元时,月销售利润最大?并求出最大利润. (2)为控制销量,大華超市提高了销售单价,在原来的基础上增加了m元,但是超市又不想让单价超过40元,超市要想得到2600元的利润,应该增加多少元? 设计意图? 二次函数的实际应用体现了二次函数模型的应用价值. 学生根据实际问题抽象出二次函数的模型,然后应用二次函数最值的性质确定获得最大利润时的单价,使数学抽象与数学建模的核心素养落地生根,在应用的过程中,提高了学生分析问题解决问题的能力. 教学感悟 梳理旧知时,要注重知识与方法并重,不仅要让学生回忆学过的知识与方法,再建知识结构,而且将知识的发生与发展的历程也作为梳理的重点. 本节课就重新梳理了一下研究函数的一般套路与程序,学生可以使用这种方法研究其他的函数,为进一步学习做好铺垫;重视数学思想方法的渗透,数学思想方法是数学知识的提炼与升华,它对数学知识的生成、研究方法的使用、解答试题的策略都有很强的指导意义,如本节复习课就向学生渗透了数形结合、分类讨论、从特殊到一般、方程思想、函数思想等;重视模型的回归应用,落实核心素养,本节课要求学生根据实际问题抽象出二次函数的模型,然后应用二次函数最值的性质确定获得最大利润时的单价,使数学抽象与数学建模的核心素养落地生根,在应用的过程中,提高了学生处理关键问题的能力.

