核心素养理念下的数学变式教学

    周琦

    

    [摘? 要] 数学变式教学是指紧扣本质特征不变这一中心思想，从不同角度，采用不同方式，变换背景，改变数学问题的表现形式，使相关问题非本质特征发生更变的一种教学方式. 教师在教学过程中应引导学生从“变”的现象中发现“不变”的本质，从而提升分析数学问题、解决数学问题的能力.

    [关键词] 变式教学;化归思想;找规律

    教材分析

    “找规律”是七年级上册，学生在学习了有理数的运算、用字母表示数和整式的加减基础上展开的一节活动课. 它既是对前面所学知识的综合运用，也是对这些知识的拓展和延伸，还能为学生今后学习方程、函数等知识奠定基础.

    教学目标

    1. 用整式表示实际问题中的数量关系.

    2. 掌握从特殊到一般的分析问题的归纳方法，以及从一般到特殊的化归问题的解决策略.

    3. 培养思辨精神和应用意识.

    教学重点

    1. 用整式表示实际问题中的变化量与n的对应数量关系.

    2. 掌握从特殊到一般、化归等数学思想方法的应用.

    教学难点

    发展学生的数学抽象、逻辑推理、数学建模等核心素养.

    教学过程

    （一）情境引入，开宗明义

    问题? 请写出1+2+3+…+n（n为正整数）的结果，并说明理由.

    解答? 1+2+3+…+n= ·n（n为正整数）

    所以1+2+3+…+n= ·n（n为正整数）.

    设计意图? “找规律”是一个覆盖面非常广的课题，在初中段，需要学生掌握一些基本数字规律和研究方法. 本课以从1开始的连续自然数的求和问题为探究主线，从不同角度和层次展开变式应用.

    追问：看到这个等式，你们有没有想到一位伟大的数学家和与此相关的故事？

    设计意图? 切合教学内容的数学文化介绍，能激发学生学习数学的兴趣和动力，从而让他们在数学求学之路上增强自信、发愤图强.

    （二）一法多题，融会贯通

    通过变换背景，改变基本方法的表现形式，可以寻找核心问题的能力增长点，从而达到理解一个基本原理，解决一类相关问题，促进数学高阶思维发展的目的.

    1. 等式问题中的变式

    变式1? 观察下列等式：

    1=12 ①

    1+3=22 ②

    1+3+5=32 ③

    1+3+5+7=42 ④

    …

    请写出第⑤个等式并验证.

    解答? 第⑤个等式为1+3+5+7+9=52.

    验证：左边=1+3+5+7+9=25，

    右边=52=25，

    所以左边=右边.

    所以等式成立.

    追问1：请写出第n个等式（n为正整数），并说明理由.

    追问2：从1开始，连续多少个奇数相加的和等于400？

    设计意图? 从探究连续自然数相加的规律，变式到探究连续奇数相加的规律，体现了数学思维的发展性和深刻性. “追问1”对一般规律的验证，考查了学生数学思维的逻辑性和严谨性;“追问2”从逆向变式的角度，提升学生对连续奇数的和与等式序号n之间对应关系的理解.

    2. 数阵问题中的变式

    变式2? 将正偶数按照图1所示的规律排列下去. 若用有序实数对（a，b）表示第a行的第b个数，如（4，3）表示偶数18，则图中（8，6）的位置表示的数是多少？

    解答? 图1中的数阵我们可以换个角度改写成图2的形式.

    用符号语言来表示第n行最后一个数，为2（1+2+3+…+n）=2· ·n=n（n+1）（n为正整数），所以第7行最后一个数为7×8=56. 所以第8行第6个数为56+2×6=68.

    追问1：求出偶数2020对应的有序实数对.

    追问2：用含n的代数式表示第n行（n≥2）的最后一个数与第（n-1）行最后一个数的差.

    设计意图? 一脉相承的研究体系，体现了由特殊到一般的研究思路和由一般到特殊的应用路径. 根据题目给出的图形、数值、数列等已知条件，发现第n行最后一个数的表达式可以转化为主线的解决策略.

    3. 图形问题中的变式

    变式3? 如图3，图①是一个水平摆放的正方体木块，图②和图③是由这样的正方体木块按一定的规律叠放而成的. 其中圖①有1个正方体木块，图②有6个正方体木块，图③有15个正方体木块……按照这样的规律继续叠放下去，图⑥有多少个正方体木块？

    解答? 图①中，正方体木块的个数为1;

    图②中，正方体木块的个数为1+5=6;

    图③中，正方体木块的个数为1+5+9=15.

    从前3个式子可以得出图⑥中正方体木块的个数为1+5+9+13+17+21=66.

    追问：图⑩中有多少个正方体木块？

    设计意图? 图形问题找规律是数形结合思想方法运用的典范. 一方面，可以从数的发展趋势寻找规律，只要前后两项的差不变，都可以用主线的方法得出一般结论;另一方面，可以从图形的构成特征寻找规律，分解、化归成基本图形并写出变化量与n的对应数量关系，再进一步化简，问题迎刃而解.

    4. 实际问题中的变式

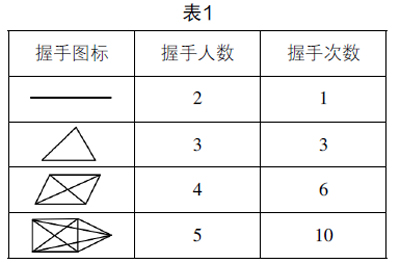
    变式4? 某次联谊会有40人参加. 若40位与会人员彼此握手一次，那么全体与会人员共握手多少次？若用点来表示每个人，连接两点的线段数目表示握手的次数，结合表1中的提示解决问题.

    解答? 由表1中的规律可知，2位与会人员彼此握手一次，共握手1次，1=0+1;3位与会人员彼此握手一次，共握手3次，3=1+2;4位与会人员彼此握手一次，共握手6次，6=1+2+3;5位与会人员彼此握手一次，共握手10次，10=1+2+3+4. 类比规律，当n位与会人员彼此握手一次时，共握手1+2+…+（n-1）= n（n-1）次. 所以当n=40时， n（n-1）= ×40×39=780.

    追问1：所有与会人员彼此握手一次，共握手435次，那么与会人员一共有多少人？

    追问2：所有与会人员彼此之间互送贺卡，40位与会人员一共送出贺卡多少张？

    设计意图? 主线的背景放置到实际问题的变式中，将每个人抽象成点，借助表格将人与人之间的握手问题抽象为点与点之间的连线段问题，实现了从实际问题到数学问题的转化. “追问1”进行思维的逆向变式，“追问2”进行对比变式，学生在情境变式中会再次体验主线规律的运用，能发展学生的数学抽象、逻辑推理和数学建模等核心素养.

    （三）集思广益，变中探源

    课堂小结环节请学生从知识、方法、经验、疑惑等方面对本节课进行变式梳理.

    设计意图? 引导学生回顾本节课用于找规律的知识，在“万变之题”中总结解决找规律问题的步骤与方法，归纳出“不变之道”——基本模型，形成解决这类问题的通法经验.

    教学反思

    本节课抓住高斯求和这条主线，从等式问题中的变式、数阵问题中的变式、图形问题中的变式、实际问题中的变式四个方面展开详述. 随着学生数学知识的增长，还可以探究几何问题中的变式、不等式问题中的变式、函数问题中的变式等，丰富变式背景，从而拓宽学生观察问题的眼界，锻炼学生思考问题的能力，并赋予数学模型不同的表现形式和存在意义. 数学模型好比人的“筋骨”，亘古不变，变换的背景就是“血肉之躯”，二者合一便造就一个个鲜活的“生命”. 因此，二者相互依存，在教學中偏废任何一方都是不可取的.

    解题是数学学习绕不开的重要环节，学生要想达到事半功倍的学习效果，教师就要沉下心来钻研教材教法，有目的有层次地精挑细选试题，合理运用变式教学，引导学生抓住“不变”的本质运用“变化”的视角灵活处理问题. 核心素养理念下的数学变式教学，不仅能使学生有效巩固所学知识，强化思想方法，而且能让他们自觉建构不同体系间的横向联系，促进他们应用意识和创新能力的发展.