确定物体重心位置的常用方法
蔡蓓蓓

一个物体的各部分都要受到重力作用,从效果上看,我们可以认为各部分受到的重力作用集中于一点,这一点叫做物体的重心.质量分布均匀、形状规则的物体,重心在它的几何中心,质量分布不均匀的物体,重心的位置除跟物体的形状有关外,还跟物体内质量的分布有关.载重汽车的重心随着装货多少和装载位置而变化,起重机的重心随着提升物体的重量和高度而变化.
确定物体重心的方法通常有以下几种,
一、几何法
质量分布均匀、形状规则的物体,重心在它的几何中心.如图1,均匀细直棒的重心在棒的中点,均匀球体的重心在球心,均匀网柱的重心在轴线的中点.
从中不难发现这样一个规律,若质量分布均匀、形状规则的物体有对称轴、对称中心、对称面,则重心必在此对称轴、对称中心、对称面上.
例1 质量分布均匀、形状规则的物体重心在它的____,为增大物体的稳定性,可以____物体重心的位置和增大物体底部的_______.
解析 重力在物体的作用点叫做重心.形状规则质量分布均匀的物体,重心在物体的几何中心;形状不规则的物体,有可能重心不在物体中心,甚至不在物体上,
提高稳定性的方法主要有两种:一是增大支承面,二是降低重心.
答案 几何中心,降低,面积.
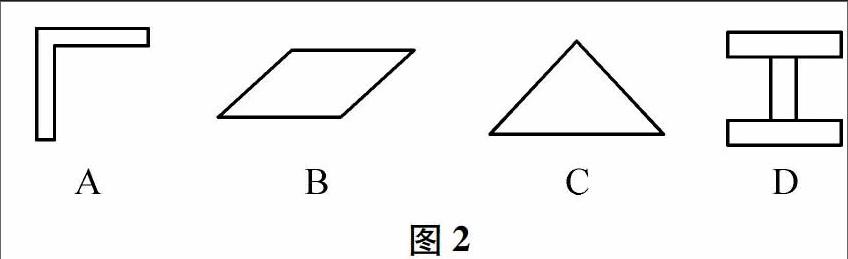
例2 下列有规则形状的物体质量分布均匀,请在图2中画出A、B、C、D各物体的重心位置.
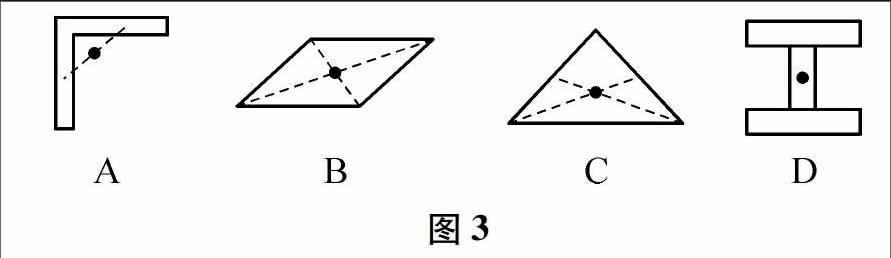
解析 分析图例根据对称性,质地均匀、形状规则的物体的重心在其几何中心上,如方形物体的重心在其几何中心,如果是方形薄物体,它的重心在两条对角线交点上.球的重心在球心,粗细均匀棒的重心在它的中点,所以各物体的重心如图3所示,
二、悬挂法
用悬挂法可以确定薄板的重心位置.首先找一根细绳,在薄板上找一点,用绳悬挂,画出薄板静止后的重力线,同理再找一点悬挂,两条重力线的交点就是物体重心.
例3 如图4所示是确定薄板重心的方法,先在A点把薄板悬挂起来,然后在C点把薄板再悬挂一次,由此可知,薄板的重心在哪里?该过程应用的物理原理是什么?
解析 重心是重力的作用点,是一个物体受重力的总效果的反映.可根据重力的方向是竖直向下和二力平衡的条件来突破此题.如图4,先在A点把薄板悬挂起来,对于静止的薄板而言,只受重力和绳子上的拉力,由于这两个力必等大反向共线,即重力与绳子处于一条直线上,因此绳子的直线通过重心(重力作用点),即薄板的重心一定在AB直线上.然后在C点把薄板再悬挂一次,同理可知,薄板的重心一定在通过C点的竖直线CD上,AB、CD的交点在O,就是薄板的中心位置.
三、支撑法
只适用于细棒(不一定均匀).如图5,用一个支点支撑物体,不断变化位置,越稳定的位置,越接近重心.
一种可能的变通方式是用两个支点支撑,然后施加较小的力使两个支点靠近,因为离重心近的支点摩擦力会大,所以物体会随之移动,使另一个支点更接近重心,如此可以找到重心的近似位置.
四、针顶法
同样只适用于薄板.用一根细针顶住板子的下面,当板子能够保持平衡,那么针顶的位置接近重心.与支撑法同理,可用3根细针互相接近的方法,找到重心位置的范围,不过这就没有支撑法的变通方式那样方便了.
五、铅垂线法(任意一图形,质地均匀)
用绳子找其一端点悬挂,后用铅垂线挂在此端点上(描下来).而后用同样的方法作另一条线.两线交点即其重心.
六、理论计算法
物体的重心,可以依据杠杆平衡原理和支撑法原理,平衡时支点处即为重心位置,



一个物体的各部分都要受到重力作用,从效果上看,我们可以认为各部分受到的重力作用集中于一点,这一点叫做物体的重心.质量分布均匀、形状规则的物体,重心在它的几何中心,质量分布不均匀的物体,重心的位置除跟物体的形状有关外,还跟物体内质量的分布有关.载重汽车的重心随着装货多少和装载位置而变化,起重机的重心随着提升物体的重量和高度而变化.
确定物体重心的方法通常有以下几种,
一、几何法
质量分布均匀、形状规则的物体,重心在它的几何中心.如图1,均匀细直棒的重心在棒的中点,均匀球体的重心在球心,均匀网柱的重心在轴线的中点.
从中不难发现这样一个规律,若质量分布均匀、形状规则的物体有对称轴、对称中心、对称面,则重心必在此对称轴、对称中心、对称面上.
例1 质量分布均匀、形状规则的物体重心在它的____,为增大物体的稳定性,可以____物体重心的位置和增大物体底部的_______.
解析 重力在物体的作用点叫做重心.形状规则质量分布均匀的物体,重心在物体的几何中心;形状不规则的物体,有可能重心不在物体中心,甚至不在物体上,
提高稳定性的方法主要有两种:一是增大支承面,二是降低重心.
答案 几何中心,降低,面积.
例2 下列有规则形状的物体质量分布均匀,请在图2中画出A、B、C、D各物体的重心位置.
解析 分析图例根据对称性,质地均匀、形状规则的物体的重心在其几何中心上,如方形物体的重心在其几何中心,如果是方形薄物体,它的重心在两条对角线交点上.球的重心在球心,粗细均匀棒的重心在它的中点,所以各物体的重心如图3所示,
二、悬挂法
用悬挂法可以确定薄板的重心位置.首先找一根细绳,在薄板上找一点,用绳悬挂,画出薄板静止后的重力线,同理再找一点悬挂,两条重力线的交点就是物体重心.
例3 如图4所示是确定薄板重心的方法,先在A点把薄板悬挂起来,然后在C点把薄板再悬挂一次,由此可知,薄板的重心在哪里?该过程应用的物理原理是什么?
解析 重心是重力的作用点,是一个物体受重力的总效果的反映.可根据重力的方向是竖直向下和二力平衡的条件来突破此题.如图4,先在A点把薄板悬挂起来,对于静止的薄板而言,只受重力和绳子上的拉力,由于这两个力必等大反向共线,即重力与绳子处于一条直线上,因此绳子的直线通过重心(重力作用点),即薄板的重心一定在AB直线上.然后在C点把薄板再悬挂一次,同理可知,薄板的重心一定在通过C点的竖直线CD上,AB、CD的交点在O,就是薄板的中心位置.
三、支撑法
只适用于细棒(不一定均匀).如图5,用一个支点支撑物体,不断变化位置,越稳定的位置,越接近重心.
一种可能的变通方式是用两个支点支撑,然后施加较小的力使两个支点靠近,因为离重心近的支点摩擦力会大,所以物体会随之移动,使另一个支点更接近重心,如此可以找到重心的近似位置.
四、针顶法
同样只适用于薄板.用一根细针顶住板子的下面,当板子能够保持平衡,那么针顶的位置接近重心.与支撑法同理,可用3根细针互相接近的方法,找到重心位置的范围,不过这就没有支撑法的变通方式那样方便了.
五、铅垂线法(任意一图形,质地均匀)
用绳子找其一端点悬挂,后用铅垂线挂在此端点上(描下来).而后用同样的方法作另一条线.两线交点即其重心.
六、理论计算法
物体的重心,可以依据杠杆平衡原理和支撑法原理,平衡时支点处即为重心位置,

