力的分解的常用方法
陈海军

一、三角函数法
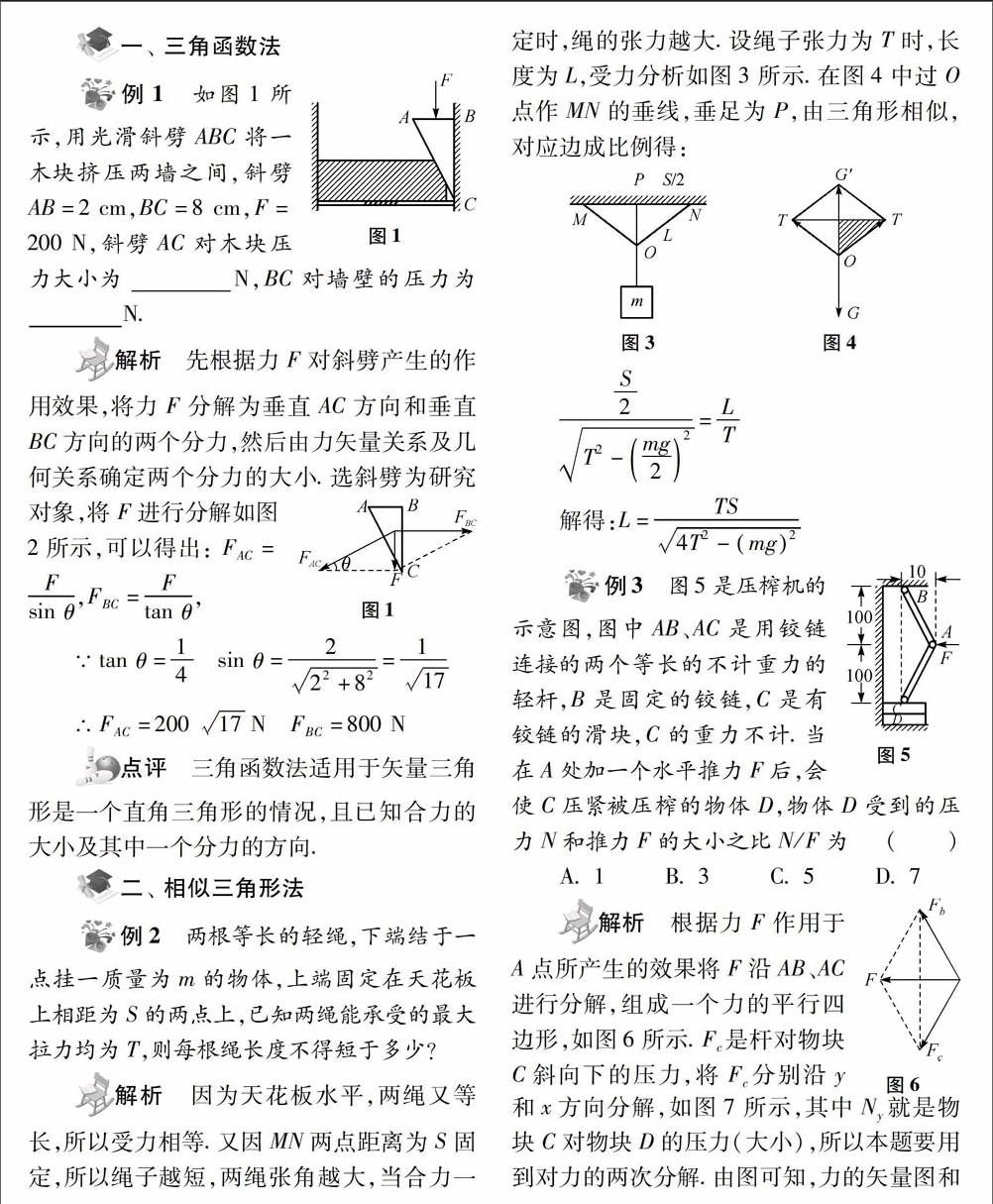
例1 如图1所示,用光滑斜劈ABC将一木块挤压两墙之间,斜劈AB=2cm,BC=8cm,F=200N,斜劈AC对木块压力大小为____N,BC对墙壁的压力为______N.
解析 先根据力F对斜劈产生的作用效果,将力F分解为垂直AC方向和垂直BC方向的两个分力,然后由力矢量关系及几何关系确定两个分力的大小.选斜劈为研究对象,将F进行分解如图2所示,可以得出:FAC=
点评 三角函数法适用于矢量三角形是一个直角三角形的情况,且已知合力的大小及其中一个分力的方向.
二、相似三角形法
例2 两根等长的轻绳,下端结于一点挂一质量为m的物体,上端固定在天花板上相距为S的两点上,已知两绳能承受的最大拉力均为T,则每根绳长度不得短于多少?
解析 因为天花板水平,两绳又等长,所以受力相等.又因MN两点距离为S固定,所以绳子越短,两绳张角越大,当合力一定时,绳的张力越大.设绳子张力为T时,长度为L,受力分析如图3所示.在图4中过0点作MN的垂线,垂足为P,由三角形相似,对应边成比例得:
例3 图5是压榨机的示意图,图中AB、AC是用铰链连接的两个等长的不计重力的轻杆,B是固定的铰链,C是有铰链的滑块,C的重力不计.当在A处加一个水平推力F后,会使C压紧被压榨的物体D,物体D受到的压力N和推力F的大小之比N/F为()
A.1
B.3
C.5
D.7
解析 根据力F作用于A点所产生的效果将F沿AB、AC进行分解,组成一个力的平行四边形,如图6所示.Fc是杆对物块C斜向下的压力,将Fc分别沿y和x方向分解,如图7所示,其中Ⅳ、就是物块C对物块D的压力(大小),所以本题要用到对力的两次分解.由图可知,力的矢量图和压榨机的杆组成相似三角形,所以我们可以根据相似三角形对应边的比相等,可以求出最后结果Ⅳ、来.先根据图示尺寸求出
点评 相似三角形适用于已知几何三角形的三个边长和合力.
三、正弦定理法
例4 重为G的物体,由两根细绳悬挂.若绳AO和BO跟竖直方向的夹角分别为α、β.试求两绳的张力.
解析 通常用正交分解法,但运算较为复杂,我们知道物体在重力G、绳的张力TA和TB三个共点力作用下平衡,故G、TA、TB可组成一封闭的力三角形.由正弦理可得:
例5 如图8所示,绳AB能承受的最大张力为1000N,轻杆BC能承受最大压力2000N,绳BD能承受任何负载,求此装置能悬挂的最大重力G.
解析 用力合成法将三个力转化在同一个三角形中,虽然几何三角形各边长度未知,但力的三角形中各角角度是已知的,故该题可用正弦定理求解.选B点为研究对象,受力分析如图9所示,绳上拉力FT,和杆对B点的支持力FN的合力与重物的重力G是平衡力,B点受三力作用而平衡,绳BD拉力等于G,BC杆支持力FN,绳AB拉力FT,三力构成封闭三角形,从图中可得:
即当FT达最大值时,FN尚未达最大值,因此取FN=1000N,计算悬挂重物G的最大值.
点评 正弦定理适用于已知力的矢量三角形的三个角和合力.
四、正交分解法
例6 如图10所示,质量为m的物体放在倾角为θ的斜面上,在水平恒定的推力F作用下,物体沿斜面匀速向上运动,则物体与斜面间的动摩擦因数是多大?
解析 物体m受四个力作用:重力mg、推力F、支持力FN和摩擦力Ff.由于物体受力较多,我们采用正交分解法解该题.建立如图11所示直角坐标系,把重力mg和推力F分别分解到x、y轴上.得:
点评 正交分解法法适用于已知合力和两个分力的方向.


一、三角函数法
例1 如图1所示,用光滑斜劈ABC将一木块挤压两墙之间,斜劈AB=2cm,BC=8cm,F=200N,斜劈AC对木块压力大小为____N,BC对墙壁的压力为______N.
解析 先根据力F对斜劈产生的作用效果,将力F分解为垂直AC方向和垂直BC方向的两个分力,然后由力矢量关系及几何关系确定两个分力的大小.选斜劈为研究对象,将F进行分解如图2所示,可以得出:FAC=
点评 三角函数法适用于矢量三角形是一个直角三角形的情况,且已知合力的大小及其中一个分力的方向.
二、相似三角形法
例2 两根等长的轻绳,下端结于一点挂一质量为m的物体,上端固定在天花板上相距为S的两点上,已知两绳能承受的最大拉力均为T,则每根绳长度不得短于多少?
解析 因为天花板水平,两绳又等长,所以受力相等.又因MN两点距离为S固定,所以绳子越短,两绳张角越大,当合力一定时,绳的张力越大.设绳子张力为T时,长度为L,受力分析如图3所示.在图4中过0点作MN的垂线,垂足为P,由三角形相似,对应边成比例得:
例3 图5是压榨机的示意图,图中AB、AC是用铰链连接的两个等长的不计重力的轻杆,B是固定的铰链,C是有铰链的滑块,C的重力不计.当在A处加一个水平推力F后,会使C压紧被压榨的物体D,物体D受到的压力N和推力F的大小之比N/F为()
A.1
B.3
C.5
D.7
解析 根据力F作用于A点所产生的效果将F沿AB、AC进行分解,组成一个力的平行四边形,如图6所示.Fc是杆对物块C斜向下的压力,将Fc分别沿y和x方向分解,如图7所示,其中Ⅳ、就是物块C对物块D的压力(大小),所以本题要用到对力的两次分解.由图可知,力的矢量图和压榨机的杆组成相似三角形,所以我们可以根据相似三角形对应边的比相等,可以求出最后结果Ⅳ、来.先根据图示尺寸求出
点评 相似三角形适用于已知几何三角形的三个边长和合力.
三、正弦定理法
例4 重为G的物体,由两根细绳悬挂.若绳AO和BO跟竖直方向的夹角分别为α、β.试求两绳的张力.
解析 通常用正交分解法,但运算较为复杂,我们知道物体在重力G、绳的张力TA和TB三个共点力作用下平衡,故G、TA、TB可组成一封闭的力三角形.由正弦理可得:
例5 如图8所示,绳AB能承受的最大张力为1000N,轻杆BC能承受最大压力2000N,绳BD能承受任何负载,求此装置能悬挂的最大重力G.
解析 用力合成法将三个力转化在同一个三角形中,虽然几何三角形各边长度未知,但力的三角形中各角角度是已知的,故该题可用正弦定理求解.选B点为研究对象,受力分析如图9所示,绳上拉力FT,和杆对B点的支持力FN的合力与重物的重力G是平衡力,B点受三力作用而平衡,绳BD拉力等于G,BC杆支持力FN,绳AB拉力FT,三力构成封闭三角形,从图中可得:
即当FT达最大值时,FN尚未达最大值,因此取FN=1000N,计算悬挂重物G的最大值.
点评 正弦定理适用于已知力的矢量三角形的三个角和合力.
四、正交分解法
例6 如图10所示,质量为m的物体放在倾角为θ的斜面上,在水平恒定的推力F作用下,物体沿斜面匀速向上运动,则物体与斜面间的动摩擦因数是多大?
解析 物体m受四个力作用:重力mg、推力F、支持力FN和摩擦力Ff.由于物体受力较多,我们采用正交分解法解该题.建立如图11所示直角坐标系,把重力mg和推力F分别分解到x、y轴上.得:
点评 正交分解法法适用于已知合力和两个分力的方向.

