弹力的方向判断及应用
潘海军

物体在力的作用下发生的形状或体积改变叫做形变.在外力停止作用后,能够恢复原状的形变叫做弹性形变.发生弹性形变的物体由于要恢复原状,对跟它接触的物体产生力的作用,这种力叫做弹力.弹力亦称“弹性力”.因物体的形变有多种多样,所以产生的弹力也有各种不同的形式.例如,一重物放在塑料板上,被压弯的塑料要恢复原状,产生向上的弹力,这就是它对重物的支持力.将一物体挂在弹簧上,物体把弹簧拉长,被拉长的弹簧要恢复原状,产生向上的弹力,这就是它对物体的拉力.不仅塑料、弹簧等能够发生形变,任何物体都能够发生形变,不发生形变的物体是不存在的,不过有的形变比较明显,能直接见到;有的形变相当微小,必须用仪器才能觉察出来.日常生活中观察到的相互作用,无论是推、拉、提、举,还是牵引列车、锻打工件、击球、弯弓射箭等,都属于弹力.
弹力方向的判断是受力分析的基础,我们学习的重点是了解常见的各种形式的弹力,具体情况有以下几种.
1 接触面的弹力:压力、支持力的方向总跟接触的面垂直.
1.1 面与面接触的弹力方向,垂直于接触面指向受力物体.如图1所示.
1.2 点与面接触的弹力方向,过接触点垂直于接触面(或接触面的切线),指向受力物体.如图2(甲、乙)所示.
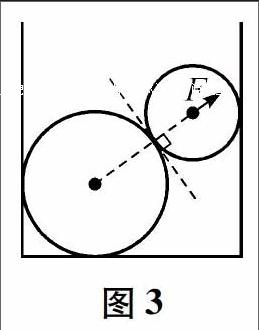
1.3 点与点的接触要找两接触点的公切面,弹力垂直于这个公切面指向被支持物.(即在两球心的连线上),而指向受力物体.如图3所示,
综上所述:①接触面是平面的,就垂直于平面;②接触面是曲面的,就垂直于曲面的切平面;③接触面是点面接触型的,就垂直于接触面,且由接触面指向受力物所在一方.
2 轻绳的弹力:绳子的拉力总是沿着绳子而指向绳子收缩的方向
“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的方向.它不能产生支持作用.它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子收缩方向的力.它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长.
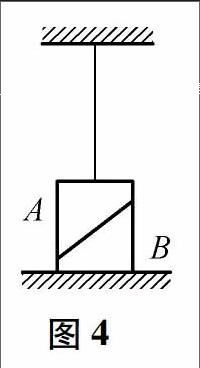
例1 将一物块分成相等的A、B两部分靠在一起,下端放置在地面上,上端用绳子拴在天花板,绳子处于竖直伸直状态,整个装置静止,如图4所示.则()
A.绳子上拉力可能为零
B.AB之间一定存在弹力
C.地面与物体间可能存在摩擦力
D.AB之间可能存在摩擦力
解析 对A分析,有4所受的重力、B对A的支持力和摩擦力三个力平衡,则绳子的拉力为零;若A只有绳子的拉力与重力,则AB间没有摩擦力存在,AB间不存在弹力,故A、D正确,B错误;对整体分析,整体可能受总重力、支持力、拉力,根据整体平衡知,在水平方向向上地面对B无摩擦力,故C错误.
3 弹簧的弹力:根据物体形变的方向判定.
轻弹簧可以被压缩或拉伸,轻弹簧各处受力相等,其方向与弹簧形变的方向相反;弹力的大小为F=kx,其中k为弹簧的劲度系数,x为弹簧的伸长量或缩短量,弹簧的弹力不会发生突变.
例2 图5中a、6、c为三个物块,M、N为两个轻质弹簧,R为跨过光滑定滑轮的轻绳,它们连接如图并处于平衡状态,下列说法正确的是()
A.有可能Ⅳ处于拉伸状态而M处于压缩状态
B.有可能Ⅳ处于压缩状态而M处于拉伸状态
C.有可能Ⅳ处于不伸不缩状态而M处于拉伸状态
D.有可能Ⅳ处于拉伸状态而朋处于不伸不缩状态
解析 由于N上面是一根绳子,因此弹簧只能处于拉伸或不伸不缩状态,不可能处于压缩状态时,a物体压轻弹簧M上,因此弹簧处于压缩状态,C错误;而当Ⅳ处于拉伸状态时,若拉力大于a的重力时,弹簧处于不伸不缩状态,AD正确.
综上所述:弹簧既可以提供拉力又可以提供推力而轻绳只能提供拉力,二者在分析时有很明显的区别,
4 杆的弹力:杆的弹力方向是任意的,由它所受外力和运动状态决定.
轻杆是一种常见的理想化物理模型,具有以下几个特征:①轻,即轻杆的质量和重力可以视为零.由此特点可知,同一轻杆的两端及其中间各点的张力大小相等.②硬,轻杆既能承受拉力也能承受压力,但其力的方向不一定沿着杆的方向.③轻杆不能伸长或压缩.
4.1 轻杆一端不固定即铰链轻杆的平衡问题
例3 如图6所示,重力是30 N的物体,由轻绳悬在水平轻质横梁BC的端点C上,横梁的B端通过铰链固定在竖直墙上,横梁上的C点由轻绳AC拉住,AC与BC夹角为30°,求悬绳AC所受到的拉力为多大?
解析 要想求AC绳所受的拉力有多大,要选C点受力分析.AC、CD两段绳的拉力一定沿绳的方向,而横杆对C点作用力的方向不好确定.这就要先看横杆BC的受力情况了,而轻质横梁的B端可自由转动,故要想BC杆能在水平位置处于平衡状态,两段绳对杆的作用力必沿杆方向,因为以B为转轴,轻杆不受重力,绳对杆的作用力只有经过转轴时力矩为零,杆才不会转动.然后再研究C点,AC和CD两绳拉力的合力必沿杆的方向,由力的合成可求出AC受到的拉力.因TD=mg,则:TA=TD/sin30°=2mg=60N.
结论铰链轻杆,即一端可以自由转动的轻杆,轻杆的作用力始终沿杆的方向.
4.2 轻杆一端固定的平衡问题
例4 水平横梁的一端插在墙壁内,另一端装有一小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量M=10kg的重物,∠CBA=30°,如图7所示,则滑轮受到绳子的作用力的大小是多少?
解析 此题与例3区别很大.杆的左端是插在墙壁内的,且另一端多了一个滑轮.这种情况下杆就不能转动了,绳对杆的作用力不沿杆的方向,杆也可以保持水平不动.而一根绳子跨过定滑轮时绳子的拉力是大小相等的,且两力夹角是120°,则它们的合力必定在这两个力的角平分线上,且与绳拉力大小相等,这时杆的作用力可以不沿杆的方向.受力如图所示,因Tw=Tc=Mg,则F合=Mg.
结论轻杆一端固定,所以杆受力不一定沿杆方向,或拉、或推、或撬,应根据实际情况分析.
4.3 相关物体做变速运动,要根据物体的运动状态判断轻杆受力
例5 如图8所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的弹力F的判断中,正确的是()
A.小车静止时,F=mgcosθ,方向沿杆向上
B.小车静止时,F=mgcosθ,方向垂直杆向上
C.小车向右以加速度。运动时,一定有F=mg/sinθ
D.小车向右以加速度a运动时,F=,方向斜向右上方,与竖直方向夹角满足tan
解析 当小车静止时小球也静止,所受重力与向上的弹力平衡,所以小球所受弹力竖直向上,大小等于m,选项A、B均错;小车向右以加速度a运动时,小球的加速度也水平向右,大小为a,小球由重力和弹力的合力产生加速度,合力为ma,由勾股定理可知,方向斜向右上方,与竖直方向夹角满足,D对
综上所述:对于轻杆受力问题,首先应明确一端是否固定.若不固定,则另一端合力必沿杆方向;若固定,则可以受任何方向的力,应根据实际情况(如受力平衡等)加以分析.
弹力的本质:弹力的本质是分子间的作用力.当物体被拉伸或压缩时,分子间的距离便会发生变化,使分子间的相对位置拉开或靠拢,这样,分子间的引力与斥力就不会平衡,出现相吸或相斥的倾向,而这些分子间的吸引或排斥的总效果,就是宏观上观察到的弹力.如果外力太大,分子间的距离被拉开得太多,分子就会滑进另一个稳定的位置,即使外力除去后,也不能再回到复原位,就会保留永久的变形.这便是弹力的本质.



物体在力的作用下发生的形状或体积改变叫做形变.在外力停止作用后,能够恢复原状的形变叫做弹性形变.发生弹性形变的物体由于要恢复原状,对跟它接触的物体产生力的作用,这种力叫做弹力.弹力亦称“弹性力”.因物体的形变有多种多样,所以产生的弹力也有各种不同的形式.例如,一重物放在塑料板上,被压弯的塑料要恢复原状,产生向上的弹力,这就是它对重物的支持力.将一物体挂在弹簧上,物体把弹簧拉长,被拉长的弹簧要恢复原状,产生向上的弹力,这就是它对物体的拉力.不仅塑料、弹簧等能够发生形变,任何物体都能够发生形变,不发生形变的物体是不存在的,不过有的形变比较明显,能直接见到;有的形变相当微小,必须用仪器才能觉察出来.日常生活中观察到的相互作用,无论是推、拉、提、举,还是牵引列车、锻打工件、击球、弯弓射箭等,都属于弹力.
弹力方向的判断是受力分析的基础,我们学习的重点是了解常见的各种形式的弹力,具体情况有以下几种.
1 接触面的弹力:压力、支持力的方向总跟接触的面垂直.
1.1 面与面接触的弹力方向,垂直于接触面指向受力物体.如图1所示.
1.2 点与面接触的弹力方向,过接触点垂直于接触面(或接触面的切线),指向受力物体.如图2(甲、乙)所示.
1.3 点与点的接触要找两接触点的公切面,弹力垂直于这个公切面指向被支持物.(即在两球心的连线上),而指向受力物体.如图3所示,
综上所述:①接触面是平面的,就垂直于平面;②接触面是曲面的,就垂直于曲面的切平面;③接触面是点面接触型的,就垂直于接触面,且由接触面指向受力物所在一方.
2 轻绳的弹力:绳子的拉力总是沿着绳子而指向绳子收缩的方向
“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的方向.它不能产生支持作用.它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子收缩方向的力.它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长.
例1 将一物块分成相等的A、B两部分靠在一起,下端放置在地面上,上端用绳子拴在天花板,绳子处于竖直伸直状态,整个装置静止,如图4所示.则()
A.绳子上拉力可能为零
B.AB之间一定存在弹力
C.地面与物体间可能存在摩擦力
D.AB之间可能存在摩擦力
解析 对A分析,有4所受的重力、B对A的支持力和摩擦力三个力平衡,则绳子的拉力为零;若A只有绳子的拉力与重力,则AB间没有摩擦力存在,AB间不存在弹力,故A、D正确,B错误;对整体分析,整体可能受总重力、支持力、拉力,根据整体平衡知,在水平方向向上地面对B无摩擦力,故C错误.
3 弹簧的弹力:根据物体形变的方向判定.
轻弹簧可以被压缩或拉伸,轻弹簧各处受力相等,其方向与弹簧形变的方向相反;弹力的大小为F=kx,其中k为弹簧的劲度系数,x为弹簧的伸长量或缩短量,弹簧的弹力不会发生突变.
例2 图5中a、6、c为三个物块,M、N为两个轻质弹簧,R为跨过光滑定滑轮的轻绳,它们连接如图并处于平衡状态,下列说法正确的是()
A.有可能Ⅳ处于拉伸状态而M处于压缩状态
B.有可能Ⅳ处于压缩状态而M处于拉伸状态
C.有可能Ⅳ处于不伸不缩状态而M处于拉伸状态
D.有可能Ⅳ处于拉伸状态而朋处于不伸不缩状态
解析 由于N上面是一根绳子,因此弹簧只能处于拉伸或不伸不缩状态,不可能处于压缩状态时,a物体压轻弹簧M上,因此弹簧处于压缩状态,C错误;而当Ⅳ处于拉伸状态时,若拉力大于a的重力时,弹簧处于不伸不缩状态,AD正确.
综上所述:弹簧既可以提供拉力又可以提供推力而轻绳只能提供拉力,二者在分析时有很明显的区别,
4 杆的弹力:杆的弹力方向是任意的,由它所受外力和运动状态决定.
轻杆是一种常见的理想化物理模型,具有以下几个特征:①轻,即轻杆的质量和重力可以视为零.由此特点可知,同一轻杆的两端及其中间各点的张力大小相等.②硬,轻杆既能承受拉力也能承受压力,但其力的方向不一定沿着杆的方向.③轻杆不能伸长或压缩.
4.1 轻杆一端不固定即铰链轻杆的平衡问题
例3 如图6所示,重力是30 N的物体,由轻绳悬在水平轻质横梁BC的端点C上,横梁的B端通过铰链固定在竖直墙上,横梁上的C点由轻绳AC拉住,AC与BC夹角为30°,求悬绳AC所受到的拉力为多大?
解析 要想求AC绳所受的拉力有多大,要选C点受力分析.AC、CD两段绳的拉力一定沿绳的方向,而横杆对C点作用力的方向不好确定.这就要先看横杆BC的受力情况了,而轻质横梁的B端可自由转动,故要想BC杆能在水平位置处于平衡状态,两段绳对杆的作用力必沿杆方向,因为以B为转轴,轻杆不受重力,绳对杆的作用力只有经过转轴时力矩为零,杆才不会转动.然后再研究C点,AC和CD两绳拉力的合力必沿杆的方向,由力的合成可求出AC受到的拉力.因TD=mg,则:TA=TD/sin30°=2mg=60N.
结论铰链轻杆,即一端可以自由转动的轻杆,轻杆的作用力始终沿杆的方向.
4.2 轻杆一端固定的平衡问题
例4 水平横梁的一端插在墙壁内,另一端装有一小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量M=10kg的重物,∠CBA=30°,如图7所示,则滑轮受到绳子的作用力的大小是多少?
解析 此题与例3区别很大.杆的左端是插在墙壁内的,且另一端多了一个滑轮.这种情况下杆就不能转动了,绳对杆的作用力不沿杆的方向,杆也可以保持水平不动.而一根绳子跨过定滑轮时绳子的拉力是大小相等的,且两力夹角是120°,则它们的合力必定在这两个力的角平分线上,且与绳拉力大小相等,这时杆的作用力可以不沿杆的方向.受力如图所示,因Tw=Tc=Mg,则F合=Mg.
结论轻杆一端固定,所以杆受力不一定沿杆方向,或拉、或推、或撬,应根据实际情况分析.
4.3 相关物体做变速运动,要根据物体的运动状态判断轻杆受力
例5 如图8所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的弹力F的判断中,正确的是()
A.小车静止时,F=mgcosθ,方向沿杆向上
B.小车静止时,F=mgcosθ,方向垂直杆向上
C.小车向右以加速度。运动时,一定有F=mg/sinθ
D.小车向右以加速度a运动时,F=,方向斜向右上方,与竖直方向夹角满足tan
解析 当小车静止时小球也静止,所受重力与向上的弹力平衡,所以小球所受弹力竖直向上,大小等于m,选项A、B均错;小车向右以加速度a运动时,小球的加速度也水平向右,大小为a,小球由重力和弹力的合力产生加速度,合力为ma,由勾股定理可知,方向斜向右上方,与竖直方向夹角满足,D对
综上所述:对于轻杆受力问题,首先应明确一端是否固定.若不固定,则另一端合力必沿杆方向;若固定,则可以受任何方向的力,应根据实际情况(如受力平衡等)加以分析.
弹力的本质:弹力的本质是分子间的作用力.当物体被拉伸或压缩时,分子间的距离便会发生变化,使分子间的相对位置拉开或靠拢,这样,分子间的引力与斥力就不会平衡,出现相吸或相斥的倾向,而这些分子间的吸引或排斥的总效果,就是宏观上观察到的弹力.如果外力太大,分子间的距离被拉开得太多,分子就会滑进另一个稳定的位置,即使外力除去后,也不能再回到复原位,就会保留永久的变形.这便是弹力的本质.

