物理图象的意义与运用
沈南杰


物理图象是通过建立坐标系来表达有关物体运动规律的一种重要方法,它能鲜明地表示物理量之间依赖关系,利用物理图象可以使问题变得简单明了.在近几年的江苏高考卷中,以图象形式出现的考题屡见不鲜,如2014年的第5题,2015年的第6、第10题等等.通过对这些考题的分析,我们不难发现,虽然考查的知识点发生了变化,但是解决图象问题的方法却是相同的.本文以运动图象为例,简要说明物理图象的意义与运用.
要解决图象问题,首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为了方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”.
(1)“轴”:纵、横轴所表示的物理量,特别要注意纵轴是位移x还是速度v.
(2)“线”:线可以反映运动性质,如x-t图象为倾斜直线表示匀速运动,v-t图象为倾斜直线表示匀变速运动.
(3)“斜率”:斜率往往代表一个物理量.x-t图象斜率表示速度.
(4)“面”即“面积”:主要看纵、横轴物理量的乘积有无意义.如x-t图象面积无意义,v-t图象与t轴所围面积表示位移,t轴上方面积表示向正方向运动位移,t轴下方面积表示向负方向运动位移.
(5)“截距”:初始条件.初始位置x0或初速度v0.
(6)“特殊值”:如交点,x-t图象交点表示相遇,v-t图象交点表示速度相等.
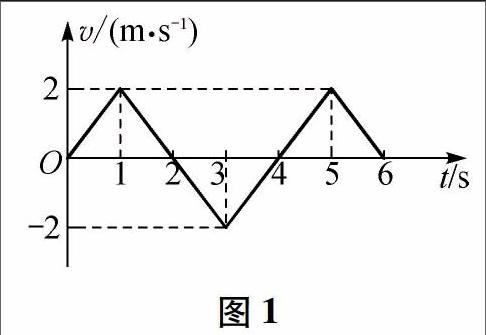
例题1质点做直线运动的速度一时间图象如图1所示,该质点
A.在第1s末速度方向发生了改变
B.在第2s末加速度方向发生了改变
C.在前2s内发生的位移为零
D.第3s末和第5s末的位置相同
基建
解析由图象可知,这是速度一时间图象(纵轴为v,横轴为t).在0-1s内,质点做匀加速直线运动(图象为倾斜直线,速度增加),1s末速度大小为2m/s,速度方向为x轴正方向(速度取正值);1-2s内,质点做匀减速直线运动,速度方向为x轴正方向(速度取正值);0-1 s内与1-2s内质点运动方向相同(v都为正),加速度方向相反(0-1s内斜率为正,1-2s内斜率为负);2-3s内质点做匀加速直线运动,3s末速度大小为2m/s,速度方向为x轴负方向(速度取负值);1-2s内与2-3s内速度方向相反,但加速度相同(直线斜率不变);3-4s内质点做匀减速直线运动,速度方向为x轴负方向;4s末后重复运动;质点在x轴上的运动过程如图2所示.质点在2s末位移达到正方向最大值(t轴上方面积达到最 4s 3s大值),大小为2m,4s末
回到出发点.
若将该图1改为x-t图,如图3所示,则质点在x轴上的运动过程如图4所示,分析方法完全相同(x-t图象面积无意义).
要解决图象问题,也要懂得如何画图.画图的依据在于物体的运动规律究竟是匀速直线运动还是匀变速直线运动或者其它.图象的形式随着问题的不同可以在x-t、v-t、a-t间变化.在画图时注意应变量与白变量之间的函数对应关系,例如匀速直线运动的x=vt,匀加速直线运动的v=v0+at、x=v0t+
,匀减速直线运动的v=v0-at、x=v0t-
,图象如图5所示,
例题2 一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.下列速度v和位移x的关系图象中,能描述该过程的是
()
解析 初速度为零的匀加速直线运动的速度与位移间函数关系是v2 =2ax,将x作为纵坐标,v作为横坐标,v-x图如图6所示.同理,将匀减速开始时刻设为t=0,匀减速直线运动的函数关系是v2-v2=-2ax,将x作为纵坐标,v作为横坐标,再将坐标变化为v-x图,如图7所示.综上所述,答案应该选A.
在掌握了识图和画图的技巧后,就可以尝试用图象来解决问题了.追及与相遇问题,板块滑动问题都可以用运动图象巧妙的解决.
例题3 经检测,汽车4的制动性能:以标准速度20 nr/s在平直公路上行驶时,制动后40s停下来.现A在平直公路上以20m/s的速度行驶时发现前方180m处有一货车B以6m/s的速度同向匀速行驶,司机立即制动,问能否发生撞车事故?
解析 由条件可得,汽车A的加速度为0.5m/S2,当两车速度相等时运动时间是28s,图中阴影部分面积为196m,两辆汽车的v-t图象如图8所示,可知不会发生撞车事故,且两车之间的最小距离是4m.
运用物理图象解决问题是高中物理解题的重要手段之一.以运动学图象为基础,逐步掌握识图、画图、用图的技巧和方法对于提高我们解决物理问题的能力有着很重要的帮助,也让我们最终能够从更多的角度去解决物理问题。



物理图象是通过建立坐标系来表达有关物体运动规律的一种重要方法,它能鲜明地表示物理量之间依赖关系,利用物理图象可以使问题变得简单明了.在近几年的江苏高考卷中,以图象形式出现的考题屡见不鲜,如2014年的第5题,2015年的第6、第10题等等.通过对这些考题的分析,我们不难发现,虽然考查的知识点发生了变化,但是解决图象问题的方法却是相同的.本文以运动图象为例,简要说明物理图象的意义与运用.
要解决图象问题,首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为了方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”.
(1)“轴”:纵、横轴所表示的物理量,特别要注意纵轴是位移x还是速度v.
(2)“线”:线可以反映运动性质,如x-t图象为倾斜直线表示匀速运动,v-t图象为倾斜直线表示匀变速运动.
(3)“斜率”:斜率往往代表一个物理量.x-t图象斜率表示速度.
(4)“面”即“面积”:主要看纵、横轴物理量的乘积有无意义.如x-t图象面积无意义,v-t图象与t轴所围面积表示位移,t轴上方面积表示向正方向运动位移,t轴下方面积表示向负方向运动位移.
(5)“截距”:初始条件.初始位置x0或初速度v0.
(6)“特殊值”:如交点,x-t图象交点表示相遇,v-t图象交点表示速度相等.
例题1质点做直线运动的速度一时间图象如图1所示,该质点
A.在第1s末速度方向发生了改变
B.在第2s末加速度方向发生了改变
C.在前2s内发生的位移为零
D.第3s末和第5s末的位置相同
基建
解析由图象可知,这是速度一时间图象(纵轴为v,横轴为t).在0-1s内,质点做匀加速直线运动(图象为倾斜直线,速度增加),1s末速度大小为2m/s,速度方向为x轴正方向(速度取正值);1-2s内,质点做匀减速直线运动,速度方向为x轴正方向(速度取正值);0-1 s内与1-2s内质点运动方向相同(v都为正),加速度方向相反(0-1s内斜率为正,1-2s内斜率为负);2-3s内质点做匀加速直线运动,3s末速度大小为2m/s,速度方向为x轴负方向(速度取负值);1-2s内与2-3s内速度方向相反,但加速度相同(直线斜率不变);3-4s内质点做匀减速直线运动,速度方向为x轴负方向;4s末后重复运动;质点在x轴上的运动过程如图2所示.质点在2s末位移达到正方向最大值(t轴上方面积达到最 4s 3s大值),大小为2m,4s末
回到出发点.
若将该图1改为x-t图,如图3所示,则质点在x轴上的运动过程如图4所示,分析方法完全相同(x-t图象面积无意义).
要解决图象问题,也要懂得如何画图.画图的依据在于物体的运动规律究竟是匀速直线运动还是匀变速直线运动或者其它.图象的形式随着问题的不同可以在x-t、v-t、a-t间变化.在画图时注意应变量与白变量之间的函数对应关系,例如匀速直线运动的x=vt,匀加速直线运动的v=v0+at、x=v0t+
,匀减速直线运动的v=v0-at、x=v0t-
,图象如图5所示,
例题2 一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.下列速度v和位移x的关系图象中,能描述该过程的是
()
解析 初速度为零的匀加速直线运动的速度与位移间函数关系是v2 =2ax,将x作为纵坐标,v作为横坐标,v-x图如图6所示.同理,将匀减速开始时刻设为t=0,匀减速直线运动的函数关系是v2-v2=-2ax,将x作为纵坐标,v作为横坐标,再将坐标变化为v-x图,如图7所示.综上所述,答案应该选A.
在掌握了识图和画图的技巧后,就可以尝试用图象来解决问题了.追及与相遇问题,板块滑动问题都可以用运动图象巧妙的解决.
例题3 经检测,汽车4的制动性能:以标准速度20 nr/s在平直公路上行驶时,制动后40s停下来.现A在平直公路上以20m/s的速度行驶时发现前方180m处有一货车B以6m/s的速度同向匀速行驶,司机立即制动,问能否发生撞车事故?
解析 由条件可得,汽车A的加速度为0.5m/S2,当两车速度相等时运动时间是28s,图中阴影部分面积为196m,两辆汽车的v-t图象如图8所示,可知不会发生撞车事故,且两车之间的最小距离是4m.
运用物理图象解决问题是高中物理解题的重要手段之一.以运动学图象为基础,逐步掌握识图、画图、用图的技巧和方法对于提高我们解决物理问题的能力有着很重要的帮助,也让我们最终能够从更多的角度去解决物理问题。

