物理模型的建构与应用
刁品全+孙铁斌


直线运动是力学问题分析的基础,也是物理奥赛题的基础部分内容.学习这部分内容对适应物理奥赛有着重要意义.这部分问题的特点主要体现在:(1)物理模型理解与构建.物理模型是物理学重要的思想方法.物理模型有实物模型,如运动中遇到的质点,我们以后还会在热学部分学到理想气体等;过程模型,如运动学中的匀速运动、匀加速运动;数学模型,建立一数学规律,如图象、函数等、等效法等,随着大家所学内容不断增加,知识不断丰富,不断总结,这样大家处理问题的能力会不断提高.(2)数学建模与数据处理能力要求加强,当我们建立物理模型后,还需要对数据进行分析,而数据分析会综合应用各种数学技巧.(3)物理问题化归与建模,这是我们中学教学中常用的技巧,这种方法其实就是将我们遇到的各类问题分成各种类型,在运动学中如追及问题、避免碰撞问题、平抛与类平抛等,
问题模型化后,可以使问题大为简化,从中较为方便地得出物体运动的基本规律.模型的建构与应用在物理学发展历史上,伟大的科学家往往都是善于提出恰当的理想模型的科学家,如爱因斯坦提出“光子说”成功地解释了光电效应现象而获得诺贝尔奖,卢瑟福提出原子的“核式结构模型”成功地解释了原子物理的一些现象,人类从而进入研究原子物理时代,同时建构主义心理学理论认为:模型的建构是心理学中人们对事物认构的心理模式.因此对初学奥赛的同学来说,了解这类问题特点尤为重要,下面我们就来举例感悟一下其中的魅力.
一、运动物理模型建立
例1 一个人在灯正下方向前匀速运动,求证人影的顶端点是做匀速直线运动.
解析 需要论证的问题是——匀速直线运动.在运动学中匀速直线运动的关键是位移与时间是一次函数关系.那么我们得找出位移与时间关系,
如图1所示,设人AB在灯0正下方向前移动至A'B',设移动距离为s,即BB',此时人影的顶端C点位置如图所示.从图可知人影的顶端C点距离还需灯与人的高度,我们
点评:本题特点之一——很多物理量未知,在这种情况下我们可以去假设,构造出数学模型,在诸多物理量之间,有的物理量可以消去,而有些物理量是恒量,物理问题尤其是物理奥赛题难就难在建立物理或数学模型.这些物理问题我们能够用图来表达的尽量先用图来描述,找出隐含的物理、数学规律.
二、相对运动模型建立
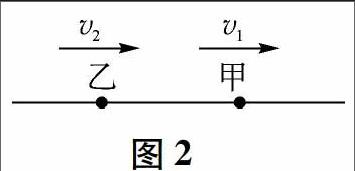
例2 如图2甲物体在前方以初速度为v1,加速度为a1,做匀加速运动,同时在甲后面s处乙初速度v2,加速为a2,做匀加速运动,问:此后甲乙可能相遇几次?
解析 按常规思路,甲、乙相遇时在空间上看位于同一位置,如果建立数学模型,也就是建立坐标轴,甲乙在该坐标轴运动过程中某时刻相遇则坐标相同,表达式有解,这就需要较强的数学功底.
其实,在运动学中讨论一个物体运动要比两个物体运动要来得更简单一些,如图2所示为甲、乙开始的位置.
那么我们不妨研究乙,以甲为参照物,则相对速度为
(1)v2-v1>0
①a2 -o.>0:这种情况也就是乙相对于甲做初速度为v2-v1、加速度为a1-a1的向右匀加速运动,显然只相遇一次.
②a2-a1=0:这种情况也就是乙相对于甲做速度为v2-v1,匀速运动,显然只相遇一次.
③a2-a1<0:这种情况也就是乙相对于甲做初速度为v2-v1、加速度为a2-a1,向右作匀减速运动,如果速度足够大则会超过甲,但会返回,这种情况类似于竖直上抛运动,这时就会相遇两次.
但速度如偏小则不相遇,也可能速度大小恰好,则相遇一次,而该临界速度为:(v2-v1)2=-2(a2-a1)s.
(2)v2-v1=0
①a2-a1>0:这种情况也就是乙相对于甲向右做初速度为0、加速度为a2-a1匀加速运动,显然只相遇一次.
②a2-a1=0:这种情况为乙相对于甲的相对速度为0、加速度为0,即相对静止,二者不可能相遇,
③a2-a1<0:这种情况是相对速度为0、而加速度为a2-a1<0的运动,由于a2-a1<0<0,则乙相对于甲是远离,那么二者不可能相遇.
(3)v2-v1<0
由于v2-v1<0,则乙相对于甲向左运动,即开始是远离运动,当
①a2-a1>0:乙向左做匀减速运动,但当速度减小为0后又向右加速运动,则甲与乙必相遇:
②a2-a1=0:乙向左做匀速运动,则甲与乙肯定不会相遇;
③a2-a1<0:乙向左做初速度为v2-v1、加速度为a2-a1匀加速运动,则甲与乙肯定不会相遇;
这种分析也许相对于单纯从数学分析思考有点烦琐,但物理意义显得更为清晰.
例3 有一小孩掉进河里后抱住了一根圆木随水向下飘流(与水流速度相等且一起运动),有三条船A、B、C在正对河岸P点的地方同时与圆木相遇,但三条船上的船员都没有注意到圆木上的小孩.A、B两船逆水上行,C船顺水下行,相对水的速度B船是A船的1.2倍,C船是B船的1.2倍.当三条船离开P点行驶30分钟的时候,船员们从收音机里听到圆木上有小孩需要救助的消息,三条船都立即调转船头,驶向圆木.在离P点6千米的地方,小孩被船员救起.试回答三条船到达小孩和圆木的先后次序如何?
解析 由于本题中涉及到A、B、C及水流(即小孩)的运动,即使通过作图也较为复杂:A、B、C三者各自都存在顺水运动与逆水运动,这样就存在六个速度,而原来在静水中还有一速度.前面我们就已讨论过借助于相对运动可以使问题简单化,由于A、B、C三者是运动是具有相似特征,而水、孩子不是我们所重点讨论的,那么我们不妨以小孩为参照物,这样水流(即小孩)就是静止状态,而A、B、C三者在远离小孩子时时间相等,运动后再各自返回,返回的距离就是原来远离小孩时的距离,那么各自所用的返回的时间与原来各自运动的时间相等,这样他们重新回到小孩位置处所用时间相等,即三条船同时到达小孩位置.
相对运动的方法在分析多个物体运动时简洁、直观,无论是匀速运动还是匀变速运动,在一条直线上还是不在一条直线上都可以用相对运动来分析,两物体速度方向不平行时相对速度计算在以后学习中可以会学习到,因此以后在分析多个物体运动时优先想到相对运动法.
三、图象模型建立与应用
图象法也是我们处理问题常用的方法,在运动学部分最常见的有速度一时间图象、位移一时间图象.在分析和应用图象时我们要充分注意到图象斜率、交点的意义,图象“面积”的意义、图象横轴和纵轴截距(即图象与横轴、纵轴交点)的意义.其实除了这些图象以外还有其它类似图象,这些图在物理学中经常用到.
例4 有甲、乙、丙三辆车以相同的速度通过A点,此后甲匀速运动、乙先匀加速后又匀减速,丙则先匀减速后匀加速,三辆车到达B点时恰好速度相等,那么哪辆车先到达B点?
解析 按照常规的思路,题目未知任何物理量的大小,我们先设出物体的初速度,经过的总位移、两个变速运动的加速度,存在两个加速时的加速度及减速时的加速度,看起来未知量太多,处理难度较大.我们不妨用运动学的速度一时间图象,图象的“面积”表示位移的大小.
如图4所示,设甲、乙、丙三者同时到达B点,从图中可见,三者在这段时间里通过的
例5 如图6、7、8三个物体甲、乙、丙分别沿所示三个光滑斜面,斜面高度相同,且两个斜面的坡面长度相等,即MN=AB+BC=OP+PQ,已知斜面倾斜角越大加速度越大、两物体分别沿两斜面滑到底端时速度大小相等,那么哪个先到达底部.位移也不等,问题关键在于乙、丙不是做的直线运动.但由于MN=AB+BC=OP+PQ,也不是说路程相等,因此我们可以作出的v-t图表示速率一时间图,那么图象的“面积”表示路程.
由于三个物体到底部时速率相等,设三个物体同时到达底部,则速率一时间图象如图9所示,从图中明显可以看出乙的“面积”最大,为了使面积相等,可以将乙时间缩短、丙的时间加长,如图10所示,这样可以保证三者“面积”相等.可见,t丙>t甲t乙,即乙先到达B点.
例6 一只老鼠从老鼠洞沿直线爬出,已知爬出的速度大小与距离老鼠洞的距离成反比,当老鼠到达距中心距离是x1=1m的A点时,速度大小为20cm/s,问当老鼠与距离老鼠洞中心是x2=2m,B点时的速度大小v2,是多少?老鼠从A点运动到B点所用时间是多少?
解析 因为老鼠从老鼠洞沿直线爬出,已知爬出的速度与通过的距离成反比,则不可能用匀速运动、匀变速运动的公式来求解,但可以通过图象法求解.因为
四、转换研究参量
在研究、分析问题时,我们习惯的思路是哪个物理量未知我们就去研究这个物理量,找出题中各种条件列出关系式,有时这种分析方法显然烦琐,而当们设一些其它中间相关量时解题反而会更加快捷,采用这种迂回的战术大大降低了分析的难度.
例7 一火车沿直线轨道从静止发出,由4地驶向B地,并停止在B地. AB两地相距x,火车做加速运动时,其加速度最大为a1.,做减速运动时,其加速度的绝对值最大为a2,由此可以判断出该火车由A到B所需的最短时间为____.
解析 我们可以通过作图知道火车运动分成两个过程,整个过程中火车先做匀加速运动,后做匀减速运动.在该过程中加速度越大、所用时间越短,两个过程时间分别为
上面解析思路清晰,但涉及到未知量较多,以时间为参量突破解题计算烦琐,但我们如果设在转折时速度为突破口,则可知:
物理模型的建构是一个难度较高的要求,但对物理有浓厚兴趣的学生尤其是要参加物理奥赛学习的同学来说,这种能力要及时自我培养,这会对自己物理学习有着极大的帮助.



直线运动是力学问题分析的基础,也是物理奥赛题的基础部分内容.学习这部分内容对适应物理奥赛有着重要意义.这部分问题的特点主要体现在:(1)物理模型理解与构建.物理模型是物理学重要的思想方法.物理模型有实物模型,如运动中遇到的质点,我们以后还会在热学部分学到理想气体等;过程模型,如运动学中的匀速运动、匀加速运动;数学模型,建立一数学规律,如图象、函数等、等效法等,随着大家所学内容不断增加,知识不断丰富,不断总结,这样大家处理问题的能力会不断提高.(2)数学建模与数据处理能力要求加强,当我们建立物理模型后,还需要对数据进行分析,而数据分析会综合应用各种数学技巧.(3)物理问题化归与建模,这是我们中学教学中常用的技巧,这种方法其实就是将我们遇到的各类问题分成各种类型,在运动学中如追及问题、避免碰撞问题、平抛与类平抛等,
问题模型化后,可以使问题大为简化,从中较为方便地得出物体运动的基本规律.模型的建构与应用在物理学发展历史上,伟大的科学家往往都是善于提出恰当的理想模型的科学家,如爱因斯坦提出“光子说”成功地解释了光电效应现象而获得诺贝尔奖,卢瑟福提出原子的“核式结构模型”成功地解释了原子物理的一些现象,人类从而进入研究原子物理时代,同时建构主义心理学理论认为:模型的建构是心理学中人们对事物认构的心理模式.因此对初学奥赛的同学来说,了解这类问题特点尤为重要,下面我们就来举例感悟一下其中的魅力.
一、运动物理模型建立
例1 一个人在灯正下方向前匀速运动,求证人影的顶端点是做匀速直线运动.
解析 需要论证的问题是——匀速直线运动.在运动学中匀速直线运动的关键是位移与时间是一次函数关系.那么我们得找出位移与时间关系,
如图1所示,设人AB在灯0正下方向前移动至A'B',设移动距离为s,即BB',此时人影的顶端C点位置如图所示.从图可知人影的顶端C点距离还需灯与人的高度,我们
点评:本题特点之一——很多物理量未知,在这种情况下我们可以去假设,构造出数学模型,在诸多物理量之间,有的物理量可以消去,而有些物理量是恒量,物理问题尤其是物理奥赛题难就难在建立物理或数学模型.这些物理问题我们能够用图来表达的尽量先用图来描述,找出隐含的物理、数学规律.
二、相对运动模型建立
例2 如图2甲物体在前方以初速度为v1,加速度为a1,做匀加速运动,同时在甲后面s处乙初速度v2,加速为a2,做匀加速运动,问:此后甲乙可能相遇几次?
解析 按常规思路,甲、乙相遇时在空间上看位于同一位置,如果建立数学模型,也就是建立坐标轴,甲乙在该坐标轴运动过程中某时刻相遇则坐标相同,表达式有解,这就需要较强的数学功底.
其实,在运动学中讨论一个物体运动要比两个物体运动要来得更简单一些,如图2所示为甲、乙开始的位置.
那么我们不妨研究乙,以甲为参照物,则相对速度为
(1)v2-v1>0
①a2 -o.>0:这种情况也就是乙相对于甲做初速度为v2-v1、加速度为a1-a1的向右匀加速运动,显然只相遇一次.
②a2-a1=0:这种情况也就是乙相对于甲做速度为v2-v1,匀速运动,显然只相遇一次.
③a2-a1<0:这种情况也就是乙相对于甲做初速度为v2-v1、加速度为a2-a1,向右作匀减速运动,如果速度足够大则会超过甲,但会返回,这种情况类似于竖直上抛运动,这时就会相遇两次.
但速度如偏小则不相遇,也可能速度大小恰好,则相遇一次,而该临界速度为:(v2-v1)2=-2(a2-a1)s.
(2)v2-v1=0
①a2-a1>0:这种情况也就是乙相对于甲向右做初速度为0、加速度为a2-a1匀加速运动,显然只相遇一次.
②a2-a1=0:这种情况为乙相对于甲的相对速度为0、加速度为0,即相对静止,二者不可能相遇,
③a2-a1<0:这种情况是相对速度为0、而加速度为a2-a1<0的运动,由于a2-a1<0<0,则乙相对于甲是远离,那么二者不可能相遇.
(3)v2-v1<0
由于v2-v1<0,则乙相对于甲向左运动,即开始是远离运动,当
①a2-a1>0:乙向左做匀减速运动,但当速度减小为0后又向右加速运动,则甲与乙必相遇:
②a2-a1=0:乙向左做匀速运动,则甲与乙肯定不会相遇;
③a2-a1<0:乙向左做初速度为v2-v1、加速度为a2-a1匀加速运动,则甲与乙肯定不会相遇;
这种分析也许相对于单纯从数学分析思考有点烦琐,但物理意义显得更为清晰.
例3 有一小孩掉进河里后抱住了一根圆木随水向下飘流(与水流速度相等且一起运动),有三条船A、B、C在正对河岸P点的地方同时与圆木相遇,但三条船上的船员都没有注意到圆木上的小孩.A、B两船逆水上行,C船顺水下行,相对水的速度B船是A船的1.2倍,C船是B船的1.2倍.当三条船离开P点行驶30分钟的时候,船员们从收音机里听到圆木上有小孩需要救助的消息,三条船都立即调转船头,驶向圆木.在离P点6千米的地方,小孩被船员救起.试回答三条船到达小孩和圆木的先后次序如何?
解析 由于本题中涉及到A、B、C及水流(即小孩)的运动,即使通过作图也较为复杂:A、B、C三者各自都存在顺水运动与逆水运动,这样就存在六个速度,而原来在静水中还有一速度.前面我们就已讨论过借助于相对运动可以使问题简单化,由于A、B、C三者是运动是具有相似特征,而水、孩子不是我们所重点讨论的,那么我们不妨以小孩为参照物,这样水流(即小孩)就是静止状态,而A、B、C三者在远离小孩子时时间相等,运动后再各自返回,返回的距离就是原来远离小孩时的距离,那么各自所用的返回的时间与原来各自运动的时间相等,这样他们重新回到小孩位置处所用时间相等,即三条船同时到达小孩位置.
相对运动的方法在分析多个物体运动时简洁、直观,无论是匀速运动还是匀变速运动,在一条直线上还是不在一条直线上都可以用相对运动来分析,两物体速度方向不平行时相对速度计算在以后学习中可以会学习到,因此以后在分析多个物体运动时优先想到相对运动法.
三、图象模型建立与应用
图象法也是我们处理问题常用的方法,在运动学部分最常见的有速度一时间图象、位移一时间图象.在分析和应用图象时我们要充分注意到图象斜率、交点的意义,图象“面积”的意义、图象横轴和纵轴截距(即图象与横轴、纵轴交点)的意义.其实除了这些图象以外还有其它类似图象,这些图在物理学中经常用到.
例4 有甲、乙、丙三辆车以相同的速度通过A点,此后甲匀速运动、乙先匀加速后又匀减速,丙则先匀减速后匀加速,三辆车到达B点时恰好速度相等,那么哪辆车先到达B点?
解析 按照常规的思路,题目未知任何物理量的大小,我们先设出物体的初速度,经过的总位移、两个变速运动的加速度,存在两个加速时的加速度及减速时的加速度,看起来未知量太多,处理难度较大.我们不妨用运动学的速度一时间图象,图象的“面积”表示位移的大小.
如图4所示,设甲、乙、丙三者同时到达B点,从图中可见,三者在这段时间里通过的
例5 如图6、7、8三个物体甲、乙、丙分别沿所示三个光滑斜面,斜面高度相同,且两个斜面的坡面长度相等,即MN=AB+BC=OP+PQ,已知斜面倾斜角越大加速度越大、两物体分别沿两斜面滑到底端时速度大小相等,那么哪个先到达底部.位移也不等,问题关键在于乙、丙不是做的直线运动.但由于MN=AB+BC=OP+PQ,也不是说路程相等,因此我们可以作出的v-t图表示速率一时间图,那么图象的“面积”表示路程.
由于三个物体到底部时速率相等,设三个物体同时到达底部,则速率一时间图象如图9所示,从图中明显可以看出乙的“面积”最大,为了使面积相等,可以将乙时间缩短、丙的时间加长,如图10所示,这样可以保证三者“面积”相等.可见,t丙>t甲t乙,即乙先到达B点.
例6 一只老鼠从老鼠洞沿直线爬出,已知爬出的速度大小与距离老鼠洞的距离成反比,当老鼠到达距中心距离是x1=1m的A点时,速度大小为20cm/s,问当老鼠与距离老鼠洞中心是x2=2m,B点时的速度大小v2,是多少?老鼠从A点运动到B点所用时间是多少?
解析 因为老鼠从老鼠洞沿直线爬出,已知爬出的速度与通过的距离成反比,则不可能用匀速运动、匀变速运动的公式来求解,但可以通过图象法求解.因为
四、转换研究参量
在研究、分析问题时,我们习惯的思路是哪个物理量未知我们就去研究这个物理量,找出题中各种条件列出关系式,有时这种分析方法显然烦琐,而当们设一些其它中间相关量时解题反而会更加快捷,采用这种迂回的战术大大降低了分析的难度.
例7 一火车沿直线轨道从静止发出,由4地驶向B地,并停止在B地. AB两地相距x,火车做加速运动时,其加速度最大为a1.,做减速运动时,其加速度的绝对值最大为a2,由此可以判断出该火车由A到B所需的最短时间为____.
解析 我们可以通过作图知道火车运动分成两个过程,整个过程中火车先做匀加速运动,后做匀减速运动.在该过程中加速度越大、所用时间越短,两个过程时间分别为
上面解析思路清晰,但涉及到未知量较多,以时间为参量突破解题计算烦琐,但我们如果设在转折时速度为突破口,则可知:
物理模型的建构是一个难度较高的要求,但对物理有浓厚兴趣的学生尤其是要参加物理奥赛学习的同学来说,这种能力要及时自我培养,这会对自己物理学习有着极大的帮助.

