整体视角下的初中数学复习课教学

2023.09.07

张维

[摘? 要] 文章以整体教学的课堂设计为载体，重视学生知识的整体构建，引领学生深度思考，形成知识体系，为后续学习奠定坚实的基础，为后续的发展提供持续的动力.

[关键词] 整体教学;复习;教学设计

复习课是回顾、组织与运用的一个综合过程. 而复习课中最重要的知识回顾不应该只是点状的、孤立的复述过程，更多地应从学科内涵与价值角度出发，指向学习结果发生发展规律，将知识串联在一起，最终形成结构化的知识. 因此我们的复习课教学设计应充分考虑与小学已学知识的联系，通过知识迁移、类比来复习与梳理初中相关知识，最终为高中及后续的学习服务.

整体构建相对完整是数学学科的重要特点，章建跃老师特别强调数学教学应该重视其整体性. 《数学课程标准》对整体性教学也提出了具体的要求：我们的教学要注重知识的生长与延伸，将各知识置于整体框架中并注重内在联系，处理好知识点之间的关系，引导学生感受数学整体美.

整体性复习课教学应注意的几个问题

复习课教学过程中容易忽视知识内在的关联性，轻视知识的形成与发展过程中的逻辑关系，不重视知识在整个教材体系中的地位和作用，出现“只见树木，不见森林”的教学状态，以致学生孤立所得的知识碎片而不能正确地应用到整体任务中，导致学习迁移度低. 所以我们的复习课要有整体架构，设计要注重整体性. 那什么是整体性教学设计？目前，还没有形成一个统一的定义，结合学者观点笔者认为，整体教学设计是构建结构的“系统”相关知识，以“学习中心”用已掌握的知识辅助学习新知识、解决新问题，将相同结构的内容关联思考、整体设计. 从整体性角度来看，以构建知识为目的，教师对学生进行有效的自我探索指导，这是教学设计完整性的核心. 那么在教师的精心指导下，如何将学生已获取的基础知识和基本方法运用到陌生的情境中去，进而实现有效迁移，便成为数学教学开展整体性教学的必要途径.

整体视野下的复习课教学设计必然关注知识的整体、结构和关联.

1. 整体性

（1）目标的整体性

《数学课程标准》从“知识技能、数学思考、问题解决、情感态度”四个维度进行阐述，它们是密切联系、相互交融的整体. 我们的复习课教学设计要始终关注四项目标的达成，始终关注“数学素养”这一总目标的达成，所以教学设计要围绕目标整体性展开.

（2）教学的整体性

初中数学复习课教学设计是通过整体构建教学来实现的. 整体教学本身是一种整体存在，整个教学过程始终围绕“整体”展开. 我们的教学设计应摆脱片段的、孤立的教学模式，关注各部分与知识结构之间的紧密联系. 构建复习课时，教师应始终强调知识间的内在联系，通过思想、方法等主线贯通知识模块，在联系中层层递进，整体构建学生的知识框架与认知结构. 对于学生的认知结构，我们要帮助其建立知识框架，整体构建，因此，我们的教学必须注重整体性.

2. 结构性

“结构性”更大程度上是由数学课程本身所决定的. 帮助学生有效构建合理的认知结构是教学的根本任务. 因此，我们的教学设计始终围绕“结构性”展开，设计促进学生建构合理的知识构建的结构化学习资源. 它主要表现在以下几个方面：

（1）数学知识结构性

数学知识之间总是存在着千丝万缕的联系，知识本身的逻辑性造就了知识之间固有的内在联系. 数学知识既包括“客观性知识”，也包括“主观性知识”. 数学的思想、方法、规律使数学知识之间实现了很好的贯通. 我们的数学复习课教学设计要紧紧围绕“数学知识结构”这一主题展开.

（2）数学认知结构性

奥苏贝尔的研究表明，教材知识构建是学生数学认知结构形成的基础. 学生的数学知识要经历重新组织和融合来纳入原有的知识结构中，所以我们的复习课教学设计要围绕数学认知结构展开，要帮助学生造就属于自己的数学认知结构. 初中生的认知结构还未达到螺旋上升，所以教学设计要针对数学认知结构性.

（3）数学教学结构化

整体教学的整体性不仅仅体现在“整体”的教学思路上，还体现在整个复习教学的结构性上. 正因为这种结构性的存在，才保证了教学的整体性存在. 教学过程的各个方面是密切相关的结构，紧扣每个结构与整体的关系使其形成一个紧固结构. 同时，教学的结构化是实现学生数学知识结构化、数学认知结构化的保障.

3. 关联性

联系是分割的结果，如果没有分割，就没有联系，而过度分割却会让数学知识变得零星、细碎. 数学教学总是期望通过零星、细碎的知识使学生的学习变得简单明了. 但问题是，分割直接导致割裂和孤立，分割的知识、分割的教学使学生头脑中的知识变得零星、细碎，难以重新组装在一起，导致调用不灵活，不能举一反三，难以融会贯通，这正是低效复习课的症结所在. 初中数学复习课教学设计，重在帮助学生回到整体，即便是部分的学习，也应将知识置于系统之中，在系统的整体轮廓下理解部分. 分割是还原论惯用的手段，只有关联才能使分割后的部分再次“还原”为整体.

关联性特征是“整体性”“结构性”的根本. 因此，關联性是初中数学复习课教学设计的核心特征，缺少了关联，整体也便不复存在了. 鉴于上述特点，我们的复习课教学设计应遵循一定的流程：首先将问题情境形成和同化成新的对象，接着由先行组织者进行类比获得整体认识，整体认识包含研究对象、研究过程和研究方法，然后进行局部研究，以问题为载体，以过程为主线，以方法为指导，最后构建知识体系，达到整体效果.

我们的教学设计只有注重整体性、结构性和关联性，才是高效的教学设计，才能更好地为教学服务，为学生服务.

构建以生为本的整体性复习课

教学设计路径

1. 借前测，忆旧知

为了了解学情，设计“直角三角形”复习的前测问题4题如下.

1. 在Rt△ABC中，直角边AC=2 cm，BC=3 cm，那么斜边AB的长度为（? ? ? ）

A. 1 cm? ? ? ? ? B. 5 cm

C. cm? ? ? D. ?cm

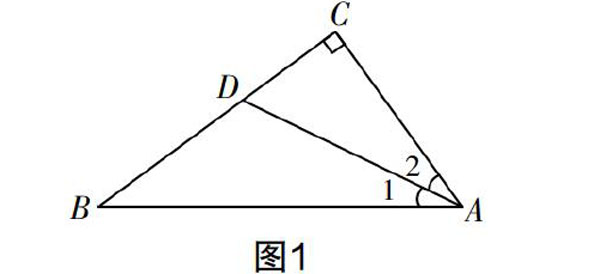
2. 如图1，在Rt△ABC中，∠ACB=90°，AD平分∠BAC交BC于点D. 如果BC=8 cm，BD=6 cm，那么点D到AB的距离为（? ? ？摇）

A. 1 cm? ? ?B. 2 cm

C. 2?cmD. 3 cm

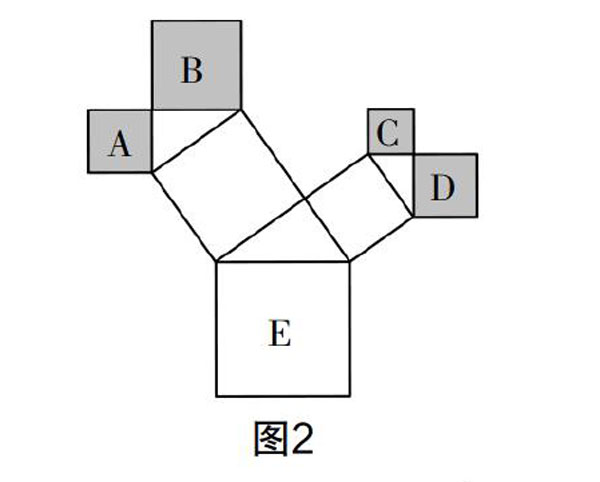
3. 如图2，勾股树中正方形A，B，C，D的面积分别为4 cm2，8 cm2，2 cm2和4 cm2，则最大的正方形E的面积为________cm2.

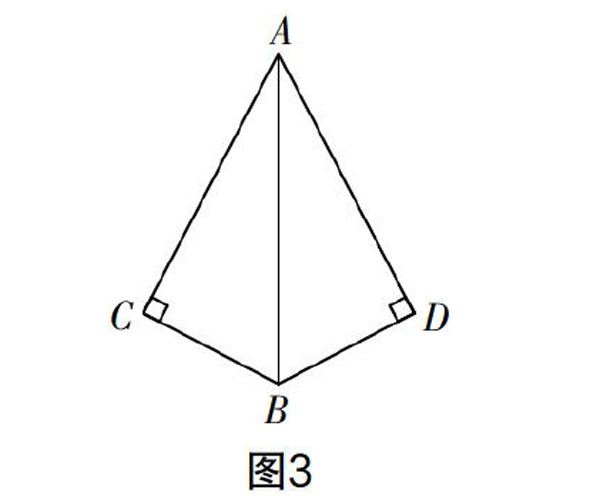
4.如圖3，若只添加一个条件，就能运用“HL”来判定Rt△ABC与Rt△ABD全等，则添加的条件是______.

设计意图通过前测，复习直角三角形的基本知识：勾股定理、直角三角形全等的证明等，以达到忆旧知的目的.

2. 练双基，促提升

问题1：如图4，给出Rt△ABC，你能得出哪些结论？这些结论有什么特殊性？

设计意图借助问题，回忆直角三角形的相关知识，但此时的知识是散状的、点状的，我们应该从边、角的方向引导、归纳，便于学生形成知识结构.

3. 解原题，提新问

（添加一个条件后再解题）

问题2：如图5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6.

（1）求△ABC的面积;

（2）过点C作CD⊥AB，垂足为D，求CD的长.

设计意图从定义和性质（边、角）两方面进行归纳.

问题3：（1）如图5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，点D是AB边上一个动点，则线段CD的取值范围是多少？

（2）如图5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，点D在AB边上，当CD为∠ACB的平分线时，求CD的长.

（3）如图6，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，点G在AC边上，当BG为∠ABC的平分线时，求BG的长.

设计意图通过问题3，引导学生对三种特殊线段进行复习，注重方法的积累与提升.

4. 炼精华，拓思维

问题4：如图7，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，AC边上有一个动点G. 沿直线BG将△BGA翻折到△BGA′，A′B与AC交于点E，当AG为何值时，△A′GE为直角三角形？

设计意图让学生从特殊线的角度构建知识体系. 熟悉直角三角形中三条新的特殊线是指斜中线=，斜高=和角平分线，原有知识结构进一步完整.

5. 重今生，续来世

通过对称轴，于横向，可由直角三角形知识过渡到等腰三角形，而等腰三角形的复习也可以从定义、性质、判定三个角度来形成框架;于纵向，过渡到平行四边形、矩形、菱形、正方形，仍用定义的属性转换，再从边、角、特殊线三个方向深入串联，最终形成知识体系. 从而达到直角三角形到等腰三角形，以及三角形到四边形的整体架构，达到几何图形认识“重今生，续来世”的目的.

结束语

注重教学设计的整体性，正如章建跃所说：教学建立在前后一致、合乎逻辑和连贯的学习过程中，使学生在掌握知识的同时学会思考，使学生有知识的整体把握，能够将零散知识进行关联与整合，友好延伸形成合理而良好的知识结构，进而生长、丰富新的认知结构，使发展学生的学习力和创新力能在复习课堂上有效落实.

因此，我们的学习过程要强调构建有层次的思维，解决拓展类问题. 整体性教学设计的实施要帮助学生避免因知识结构缺乏认识而产生孤立、分割的散状学习;要帮助学生避免“未能顾及知识的前后联系”而将教学内容以点状形式进行传递;要帮助学生进行有效的学习，提升数学品质和素养;要帮助学生在后续的学习过程中奠定坚实的知识和能力.