关于“图形的旋转”的教学设计与探讨

    葛余芳

    

    

    

    [摘? 要] “图形的旋转”是“空间与图形”领域的重要内容，教学中需要联系生活实际，让学生感知旋转;通过辨析探讨，完成概念定义;开展演示探究活动，掌握旋转性质;渗透数学思想，提升学生思维. 文章基于上述四个方面开展教学探讨，精设教学环节，与读者交流学习.

    [关键词] 图形;旋转;概念;性质;探究

    “图形的旋转”是苏教版八年级上册的重要内容，图形旋转是初中数学需要掌握的三大图形变换之一，同属“空间与图形”领域. 其中旋转的概念和性质是探究的重点，除了需要掌握上述重点知识外，还需要培养学生空间几何观，学会用变化的观念来分析问题，提升相应的数学思维. 该章节的动态内容对于学生而言，理解起来存在一定的难度，教学中建议遵循“学生为主体，教师为主导，数学活动为主线”的指导思想，采用知识探究的教学方式.

    联系实际，新知引入

    “图形的旋转”是继平移、翻转后需要学生掌握的另一种图形变换，教学引入阶段可以参考前面两大知识内容，充分联系实际，从学生接触、观察到的事物和现象出发，利用具体、感性的实物来初步认识旋转.

    引入阶段可以设置两个实践活动，包括利用多媒体演示生活中常见的与旋转相关的图片，以及借助教具近距离展示图形旋转.

    活动一：利用多媒体展示图1所示生活中的一些旋转现象.

    活动二：准备一把常用的直角三角板，教师演示直角三角板绕着直角顶点旋转，让学生观察直角板旋转的过程.

    教学指导：（1）引导学生观察上述图形变化，对比平移、翻转，分析是否与之前学习的相同，并举例生活中其他的旋转现象;（2）分析上述动图及直角板移动过程，引导学生从移动距离和转动角度来确定这种变化.

    学生对图形旋转还很陌生，利用动图展示和实物旋转的方式，学生可以直观地认识旋转与平移、翻转不同，积累相关的认识经验. 同时由具体中抽象，由感性到理性过渡的过程有助于学生后续利用理论来分析实际，进而为后续的概念、性质的探索做铺垫.

    辨析探讨，概念生成

    理解旋转的概念、掌握旋转的三要素是教学的重要内容之一，也是生活实际向数学理论的重要过渡. 旋转的概念与生活实际联系紧密，三要素是数学上对旋转本质特征的定义，因此教学中需要分为图形旋转分析和数学定义两个阶段，结合学生的认知能力，教学中建议利用平面直角坐标系，采用“引导设问”的方式提取旋转的三要素，完成概念定义.

    1. 直观呈现，感知差异

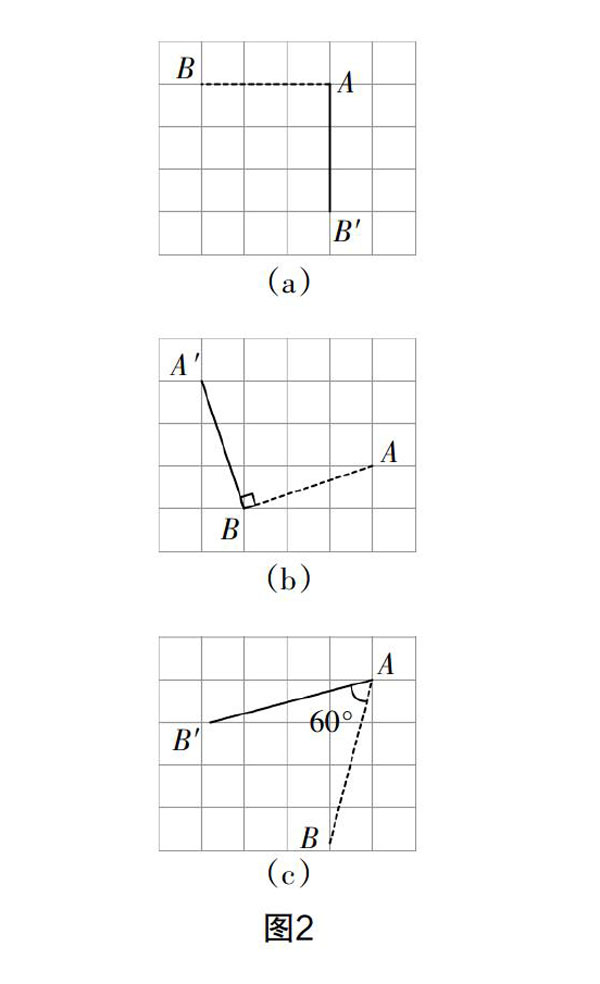
    活动：利用投影在屏幕上展示3条旋转的线段，逐一演示线段绕着点A逆时针旋转90°、绕着点B逆时针旋转90°、绕着点A顺时针旋转60°，如图2所示.

    直角坐标系可以对线段进行定位，因此有利于学生观察图形变化，在设计时建议针对旋转的三要素展开多类别呈现，变换旋转中心、旋转方向和旋转角度，引导学生全面认识旋转.

    2. 设问引导，分析要素

    通过上述线段在直角坐标系中的旋转，学生对其有了直观的感受，教学中有必要围绕旋转的三要素进行分析讨论，理解旋转过程，掌握旋转概念.

    设问1：对比图（a）和图（c），观察两条线段旋转过程有何相同点？（均围绕点A旋转）

    设问2：对比图（a）和图（b），观察两条线段的旋转方向是否相同？（旋转方向不一致）

    设问3：对比图（b）和图（c），观察两条线段的旋转角度是否相同？（旋转角度不一致）

    教学中通过对比分析的方式，引导学生关注图形旋转过程中的“旋转中心”“旋转方向”和“旋转角度”，然后结合三要素来概括旋转的概念，即在平面内，将一个图形绕着一个定点转动一定的角度，这样的图形运动称为图形的旋转，这个定点称为旋转中心，旋转的角度称为旋转角.

    3. 控制变量，理解内涵

    “旋转中心”“旋转方向”和“旋转角度”是旋转的三要素，三要素的综合才能诠释旋转的概念. 在教学中需要强调三要素之间的关系，理解其内涵，可以设计定向活动，使学生理解“三要素”缺失其中任何一个图形旋转的情形均不唯一. 可以设计如下活动并思考，准备一个△ABC，进行如下操作：

    （1）让三角形围绕点A旋转30°，可以得到怎样的情形，旋转后的位置是否唯一？

    （2）让三角形分别围绕点A和点B进行逆时针旋转，旋转角度为30°，旋转后的图形位置是否唯一？

    （3）让三角形绕着点A逆时针旋转，分析旋转后的图形位置是否唯一？

    （4）思考给定哪些条件才可以确保图形旋转后的位置唯一？

    上述活动通过缺失条件可使学生认识到“三要素”缺一不可，深刻理解图形旋转概念的内涵，为后续的性质学习提供条件.

    整体演示，性质探究

    图形旋转的性质同样是该部分探究的核心，对于后续几何旋转问题的突破有着关键作用. 图形旋转是动态变化的过程，提取性质实则就是探究旋转中的不变性，因此教学中需要设计活动呈现图形整体变化的过程，引导学生分析图形旋转前后的不变性质.

    设置如下两个探究活动：

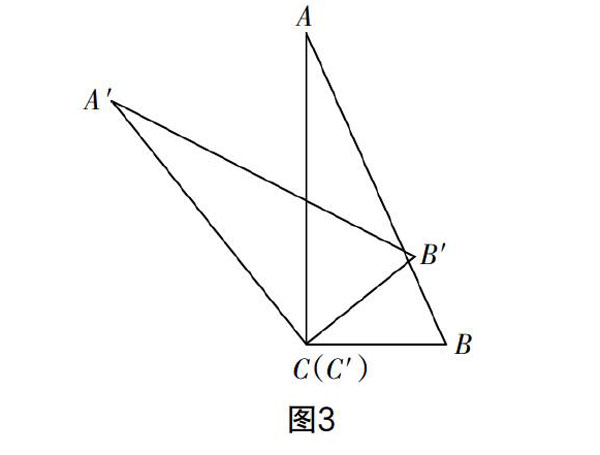
    活动一：利用直角三角形教具，设定为△ABC，用图钉固定一点C为旋转中心，将△ABC围绕点C按照逆时针的方向进行旋转，旋转后设定为△A′B′C′，如图3所示，让学生思考图形旋转前后的哪些性质有改变，哪些性质没有改变.

    引导学生思考时关注旋转过程中的两点：一是位置，二是三角形的特性. 学生很容易可以发现仅是圖形的位置发生了变化，而三角形的大小和形状没有变. 为使学生深入理解旋转时对应点、线的变化，还需深入呈现旋转的轨迹，引入旋转角度，探究旋转过程中角度、线段长的相关性质.

    活动二：呈现△ABC绕平面内一点O旋转任意角度的过程，并绘制对应点的旋转轨迹，如图4所示. 分析图形上每个顶点、边长的旋转角度是否相同，对应的顶点到点O的距离是否相同，你可以得出怎样的结论？

    引导学生标出旋转前后的对应边和对应点，然后提取对应边和对应点的旋转角度，进而得出结论;也可以随机在图形上取一点，以及旋转后的对应点，让学生观察其转化角度.

    根据上述两个活动，学生对图形旋转的性质必有一个初步的了解，性质归纳时引导学生从以下两方面进行：（1）整体上，图形的大小和形状;（2）局部中，对应点到旋转中心的距离，对应点的旋转角度. 通过实践、观察、归纳等探究活动，学生可以积累众多与旋转本质属性相关的经验，在此基础上进行分类归纳性质更为条理、清晰，也有助于提升学生的探究能力.

    渗透思想，发展思维

    “着眼生活实际，体验探究过程，发展数学思维”是该章节对学生情感方面的要求. 在旋转概念、性质的教学中需要合理渗透数学思想，提升学生的综合素养. 本章节的教学需要渗透的思想有模型思想、数形结合思想、抽象思想、归纳思想等.

    模型思想和抽象思想则主要体现在教学引入阶段，需要联系实际，基于实际问题来抽象问题模型. 例如，对于图5中的时钟，设定其中心为O，指针为线段OP，旋转后到达OP′的位置. 则可以构建线段OP围绕旋转中心O顺时针旋转∠POP′的旋转过程. 数形结合思想主要渗透在旋转性质的探究中，根据图形的旋转过程可以绘制图形的旋转轨迹，根据图像则可以获得相应的几何关系，包括线段长、角度、图形形状等. 如图6中△ABC顺时针旋转α得到了△A′B′C′，根据图像可知如下关系：△ABC≌△A′B′C′，AB=A′B′，AC=A′C′，BC=B′C′，∠AOA′=∠BOB′=∠COC′，从而完成图形旋转到等量关系的提取. 而最后的概括中体现了归纳思想，上述利用高度凝练的语言对旋转的概念和性质进行了概括，如结合三要素的核心内容来概括旋转的定义，根据旋转特性的不变量关系来概括其性质.

    这些数学思想对于提升学生的思维有着极大的帮助，数学的探究活动是低层次的，学生仅可以从中获得一些较为“粗糙”的经验，但渗透了数学思想的实践活动则可以将活动经验与人的心智、情感、思维相关联，丰富活动内容，提升活动层次，培养学生的学科素养.

    综上，对“图形的旋转”章节内容进行了新知引入、概念探讨、性质探究以及思想渗透，从生活经验中凝练知识，在觀察、分析中获得了旋转的概念和性质. 一系列的探究活动有效提升了学生发现、分析、解决问题的能力，充分感受到图形旋转的魅力，从而获得深入学习的动力.