多目标规划在黑龙江地质灾害应急物资调运中的应用

    王强 任泽洙 徐惠坚 张瑜

    

    

    

    摘? ?要：通过针对黑龙江省地质灾害的特点和赈灾物资的生产、调运情况，通过对多产品、多阶段供应链最优运作决策问题进行建模，并以实例计算证明应急物流算法的优越性与有效性。同时，通过对对偶问题进行分析，为各应急物流参与主体实现最大效益值提出了合理建议。

    关键词：灾害应急物流;供应链管理;多目标规划

    中图分类号：F252? ? ? 文献标志码：A? ? ? 文章编号：1673-291X（2019）35-0037-03

    引言

    黑龙江省地处我国北部边陲，全省共有地质灾害隐患点2 344处，其中崩塌615处、水土侵蚀620處、不稳定斜坡446处、泥石流204处、塌岸209处、地面塌陷210处、滑坡32处、地裂缝8条，地质灾害区域分布具有较明显的空间特征。受地形地貌、地质条件和人类工程活动影响，有五类灾害分布区：丘陵山地崩塌、滑坡、泥石流为主的地质灾害分布区，四大煤城地面塌陷为主的地质灾害分布区，江河沿岸塌岸为主的地质灾害分布区，山前台地、丘陵前缘水土侵蚀为主的地质灾害分布区，平原地区缓变性的地质灾害为主的分布区。2006—2014年共发生地质灾害21起。地质灾害发生之后，应急物资调运是应急救援的主要工作之一，强化供应链管理能力关系到安全监管部门和应急救援部门对于赈灾指挥决策的及时性和准确性，更关系到应急救援队伍的整体救援能力。

    从黑龙江省地质灾害分布及其产生因素看，突发性地质灾害种类主要是崩塌、不稳定斜坡、泥石流和地面塌陷为主。灾害发生之后，灾区急需物资往往为单一物资，如发电机、帐篷、饮用水、方便面、毛毯（被子）、手电筒、消毒用品等。除应急物资集散部门能够批量采购的成品外，发电机、帐篷、饮用水、毛毯（被子）、消毒用品等，该省均有较快速独立生产能力。同时，因赈灾时间紧迫，该省能够快速独立生产的产品往往由单一制造商进行生产，并由一个物资集散部门进行调运，单一制造商和单一集散部门便构成了一条单一类型的供应链。针对单一类型供应链，国内一些学者采用了目标规划思想进行管理决策建模，但这些模型对约束条件往往缺乏应有的针对性思考。考虑到黑龙江省地质灾害应急供应链上各决策者的决策将影响到其他决策者目标函数的实现问题，所以本文采用了双层多目标规划的思想来实现最优物资调运决策模型的构建，并对对偶问题进行了充分的讨论。

    一、问题描述

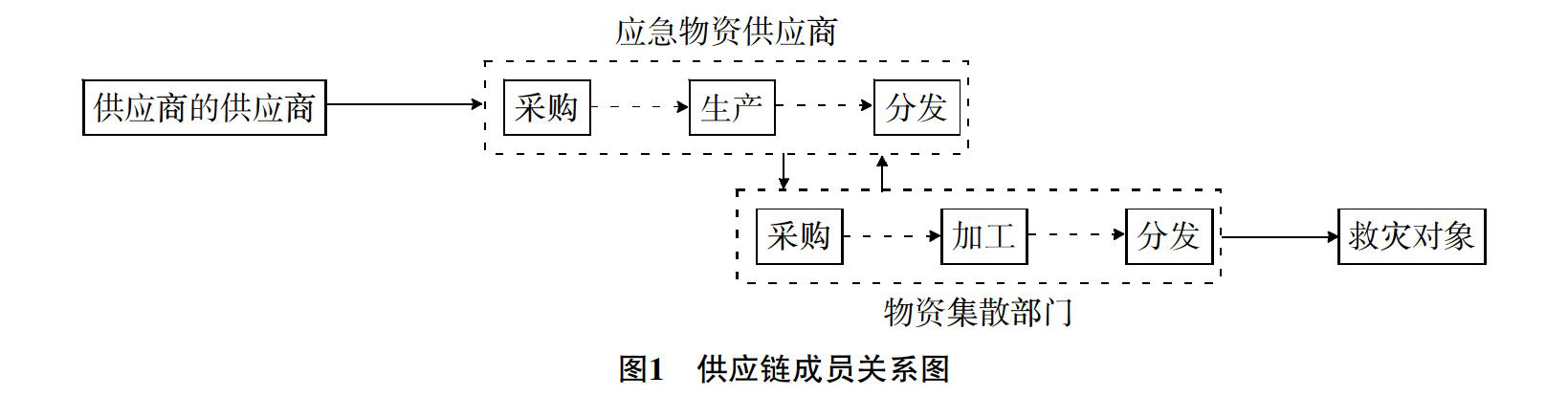
    本文所研究供应链结构如图1所示。

    （一）符号说明

    下标：j—集散部门的最终产品，j=1，2，…，J;i—集散部门的分包原料（物资供应商的产品），i =1，2，…，I;h—物资供应商的原材料，h=1，2，…，H;t—阶段，t=0，1，2，…，T（0表示初始阶段）。

    上标：s代表销售，p代表制造，w代表库存，b代表订购，v代表价格，c代表成本，r代表消耗，l代表损失，i代表效益值，max代表最大值，2代表该量与产品有关，1代表该量与原料有关。

    （二）模型描述

    为保证供应链参与主体间的协调性、连续性，假定物资供应商的交付量不低于集散部门的订购量。同时以追求过剩交付量尽可能小为目标（这样可降低库存成本），用模型表示如下：

    其中，P1为优先因子，是一个任意大的常数，M是一个给定的正数，作为供应链追求的总效益值，d+、d-为供应链实际效益值对于M的超过量与不足量。

    设效益值为第一优先级，则P1>>P2且目标函数有如下形式：

    除以上目标约束外，还需要以下系统约束：

    集散部门各阶段生产能力：

    集散部门各阶段产品库存：

    集散部门各阶段原料库存：

    物资供应商各阶段生产能力：

    物资供应商各阶段产品库存：

    物资供应商各阶段原料库存：

    各阶段物资供应商的原料的供应：

    二、应用举例

    为验证模型的优越性与合理性，对各参数赋值如下：

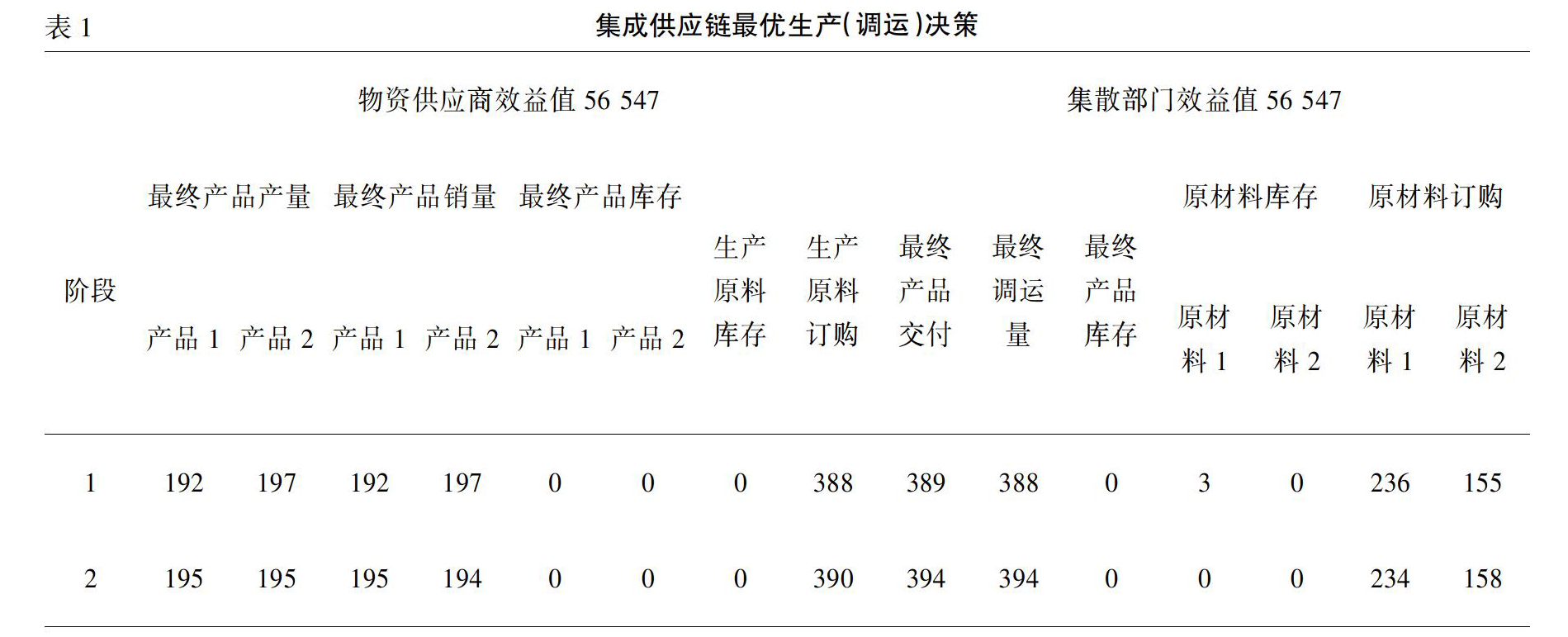
    利用以上数据，通过使用MATLAB运算，获得集成供应链最优生产（调运）决策如表1所示。

    表1中产品2在第二阶段的产量比供应量大1，而库存仍为0，是由于四舍五入的缘故，其余类似的现象解释相同。

    从效益值方面看，模型所提供的决策实现了供应链参与主体的双赢。通过对比决策方案与初始参数值可知效益值之和已经达到最大，因为原材料市场对于原材料的供应量已被充分利用，而产品的市场容量、生产能力及库存能力并未对产品的销售（调运）、生产及库存构成约束，且各库存量已达到最小（说明过剩交付量也已达到最小）。

    “零库存”本应作为决策目标之一体现在模型中，但由效益值最大化及过剩交付量最小化共同保证了库存量最小化，这体现了经营目标间的交互影响。

    三、对偶问题

    运用MATLAB解上述应用举例中问题的对偶问题（由于篇幅所限，在此不再列出对偶问题），所得目标函数的最优值与原问题目标函数最优值相同，由对偶理论知，原问题与对偶问题所得解均为最优解，基于影子价格理论可作出如下决策：

    14个对偶变量的取值为零，所以这14个对偶变量所对应的资源在生产中未被充分利用，因而不需要购进这14种资源。它们是集散部门的调运能力、产品库存能力、原料库存能力，物资供应商的生产能力、产品库存能力、原料库存能力，原材料市场上原材料2在第一、二阶段的供应量。对于生产能力及库存能力中未利用部分，可以出租以获利，闲置则会付出维护费用。

    原材料市场上，原材料1在第一、二阶段的供应约束所对应的对偶变量的绝对值，分别为99 480 000、94 980 000，表明原材料1在两个阶段的影子价格远高于市场价格30、35，这时应该购进这种资源以扩大生产，从而获取更多效益值。但此时原材料市场已无法提供更多的原材料1，这也是影子价格会如此高的原因。

    四、结论

    从以上讨论中可以看出，该模型为整条供应链的运作提供了最优决策，表明了模型的优越性与合理性。对于对偶问题的分析可以为企业（集散部门）的决策提供更多的思路，可以使企业（集散部门）的生产（调运）能力、库存能力得到充分利用，从而最大限度地获取效益值。针对黑龙江省突发性地质灾害种类主要是崩塌、不稳定斜坡、泥石流和地面塌陷为主，灾害发生之后，发电机、帐篷、饮用水、毛毯（被子）、消毒用品该省均有快速制作生产能力，使用该模型必将有助于提高赈灾物资生产、调运能力，有利于提升防灾减灾救灾能力，确保人民群众生命财产安全和社会稳定。

    参考文献：

    [1]? 史成东.集成供应链管理的多目标规划研究[J].计算机工程与应用，2009，（9）：33-36.

    [2]? 徐家旺，黄小原.市场供求不确定供应链的多目标鲁棒运作模型[J].系统工程理论与实践，2006，（6）：35-40.

    [3]? 常良峰.供应链优化及主从对策问题应用研究[D].沈阳：东北大学，2003.

    [4]? 黑龙江地质环境特征与主要地质灾害[J].中国地质灾害与防治学报，2011，（9）：101-105.

    [5]? Chopra S，Meindi P.Supply Chain Management：Strategy，Planning and Operation[M].Upper Saddle River，NJ：Prentice-Hall，2001.

    [6]? Grout J R.A Model of Incentive Contracts for just-in-time Delivery[J].European Journal of Operational Research，1996，（96）：139-147.