正交分解法的另类用途
李斌

相对速度的求解问题是高中物理学习中一个难以回避的难点,常常困扰了很多学生,尤其是高一的初学者,对矢量运算法则尚未能熟练运用,更加难以人手.本文尝试用正交分解法给出一个求相对矢量的另类途径.
一、求相对矢量的一般方法
图1所示的矢量分别为A、B.若求A相对B的矢量,则一般解法为:将矢量B平移,使B的矢尾与A的矢尾相连;B的矢端指向A的矢端的矢量,即为4相对B的矢量C,如图2所示.该方法称作矢量加减的三角形法则.在平时的教学实践中,笔者发现学生在用此法时常常出错,其原因或是此法难记易忘,或是矢量求和与矢量求差相混淆.
3.先分解再合成的相对量求解
1、2中相对量求解易于掌握,因此我们想到:对于不在同一直线上的矢量A、B的相对量,可以将A、B分解到x与y轴上,分别求出x、y轴上的分矢量的相对量,再将两个分相对矢量合成得到最后的相对量.图7所示得到两个分相对矢量,图8所示为分相对量合成后的相对量.
由上可见,正交分解法把矢量相减转化为同一直线上的矢量运算,因而容易理解并掌握.
三、相关案例的讨论
以下三道例题均涉及相对量的求解.本文止于提供正交分解的思路帮助突破题目障碍,读者可以自己解完相关题目.
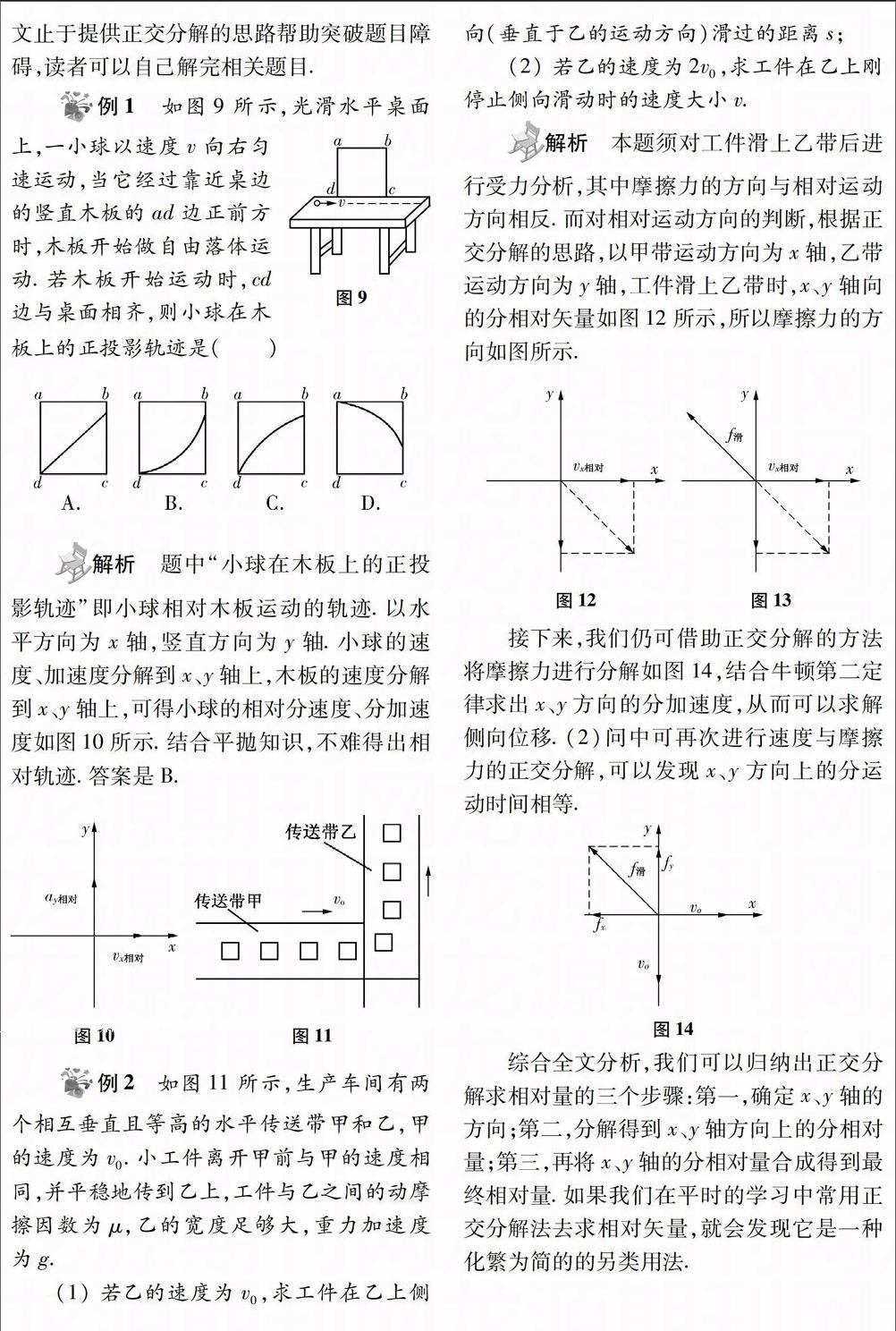
例1 如图9所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板的ad边正前方时,木板开始做自由落体运动.若木板开始运动时,cd边与桌面相齐,则小球在木板上的正投影轨迹是(
)
解析 题中“小球在木板上的正投影轨迹”即小球相对木板运动的轨迹.以水平方向为x轴,竖直方向为y轴.小球的速度、加速度分解到x、y轴上,木板的速度分解到x、y轴上,可得小球的相对分速度、分加速度如图10所示.结合平抛知识,不难得出相对轨迹.答案是B.
例2 如图11所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0.小工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与乙之间的动摩擦因数为μ,乙的宽度足够大,重力加速度为g.
(1)若乙的速度为v0,求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s;
(2)若乙的速度为2vo,求工件在乙上刚停止侧向滑动时的速度大小v.
解析 本题须对工件滑上乙带后进行受力分析,其中摩擦力的方向与相对运动方向相反.而对相对运动方向的判断,根据正交分解的思路,以甲带运动方向为x轴,乙带运动方向为y轴,工件滑上乙带时,x、y轴向的分相对矢量如图12所示,所以摩擦力的方向如图所示.
接下来,我们仍可借助正交分解的方法将摩擦力进行分解如图14,结合牛顿第二定律求出x、y方向的分加速度,从而可以求解侧向位移.(2)问中可再次进行速度与摩擦力的正交分解,可以发现x、y方向上的分运动时间相等.
综合全文分析,我们可以归纳出正交分解求相对量的三个步骤:第一,确定x、y轴的方向;第二,分解得到x、y轴方向上的分相对量;第三,再将x、y轴的分相对量合成得到最终相对量.如果我们在平时的学习中常用正交分解法去求相对矢量,就会发现它是一种化繁为简的的另类用法.


相对速度的求解问题是高中物理学习中一个难以回避的难点,常常困扰了很多学生,尤其是高一的初学者,对矢量运算法则尚未能熟练运用,更加难以人手.本文尝试用正交分解法给出一个求相对矢量的另类途径.
一、求相对矢量的一般方法
图1所示的矢量分别为A、B.若求A相对B的矢量,则一般解法为:将矢量B平移,使B的矢尾与A的矢尾相连;B的矢端指向A的矢端的矢量,即为4相对B的矢量C,如图2所示.该方法称作矢量加减的三角形法则.在平时的教学实践中,笔者发现学生在用此法时常常出错,其原因或是此法难记易忘,或是矢量求和与矢量求差相混淆.
3.先分解再合成的相对量求解
1、2中相对量求解易于掌握,因此我们想到:对于不在同一直线上的矢量A、B的相对量,可以将A、B分解到x与y轴上,分别求出x、y轴上的分矢量的相对量,再将两个分相对矢量合成得到最后的相对量.图7所示得到两个分相对矢量,图8所示为分相对量合成后的相对量.
由上可见,正交分解法把矢量相减转化为同一直线上的矢量运算,因而容易理解并掌握.
三、相关案例的讨论
以下三道例题均涉及相对量的求解.本文止于提供正交分解的思路帮助突破题目障碍,读者可以自己解完相关题目.
例1 如图9所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板的ad边正前方时,木板开始做自由落体运动.若木板开始运动时,cd边与桌面相齐,则小球在木板上的正投影轨迹是(
)
解析 题中“小球在木板上的正投影轨迹”即小球相对木板运动的轨迹.以水平方向为x轴,竖直方向为y轴.小球的速度、加速度分解到x、y轴上,木板的速度分解到x、y轴上,可得小球的相对分速度、分加速度如图10所示.结合平抛知识,不难得出相对轨迹.答案是B.
例2 如图11所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0.小工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与乙之间的动摩擦因数为μ,乙的宽度足够大,重力加速度为g.
(1)若乙的速度为v0,求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s;
(2)若乙的速度为2vo,求工件在乙上刚停止侧向滑动时的速度大小v.
解析 本题须对工件滑上乙带后进行受力分析,其中摩擦力的方向与相对运动方向相反.而对相对运动方向的判断,根据正交分解的思路,以甲带运动方向为x轴,乙带运动方向为y轴,工件滑上乙带时,x、y轴向的分相对矢量如图12所示,所以摩擦力的方向如图所示.
接下来,我们仍可借助正交分解的方法将摩擦力进行分解如图14,结合牛顿第二定律求出x、y方向的分加速度,从而可以求解侧向位移.(2)问中可再次进行速度与摩擦力的正交分解,可以发现x、y方向上的分运动时间相等.
综合全文分析,我们可以归纳出正交分解求相对量的三个步骤:第一,确定x、y轴的方向;第二,分解得到x、y轴方向上的分相对量;第三,再将x、y轴的分相对量合成得到最终相对量.如果我们在平时的学习中常用正交分解法去求相对矢量,就会发现它是一种化繁为简的的另类用法.

