将命题交给学生,让课堂在作业中延伸
李华


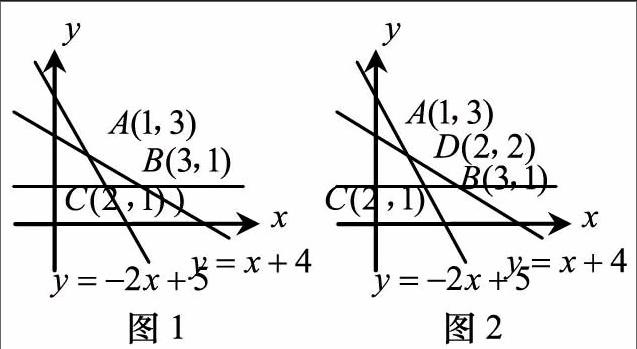
作为课堂教学的反馈和延伸,作业设计是教学环节的一个重要组成部分,提高作业设计的针对性、层次性、创新性是提高教学实效性的重要环节.目前作业形式较广泛使用的是学校根据学情编写的导学案、校本作业等,笔者在实践中探索并尝试了由学生自主命题、解答、批改的开放式作业设计,
题后反思是纠错、总结、提升的有效途径,而这些反思心得往往需要及时地回到实际问题中通过练习进一步检验和巩固,这一后续环节通常我们会为学生设计好题组或变式.笔者在某次习题课的作业设计中尝试让学生以例题为题源,通过整理做过的同类题、查阅教辅教参或者自行改编等方式,生成一道检测题或变式题,收获了意外的惊喜,
解析方法1目标函数的几何意义(略);
方法2转化为单变量函数(略);
小结(生1)目标函数非线性时,最值点不一定在平面区域的顶点;
(生2)若目标函数具有较明显的几何意义,可以通过数形结合的方法求出最值点;
(生3)若目标函数的几何意義不明显,可以从函数的角度,转化为单变量函数.
各学习小组由该题源出发选题甚至改题、编题,提交的当日作业形成了一个题组.笔者将其中质量较高的题组成一份检测卷作为第二天的作业,如:其中一个小组将题源条件保持不变,问题稍加修改成以下的变式l,并分别给出两种方法的解答过程;另一小组则认为,虽然目标函数的几何意义可以从图形快捷地得到最值点,但更多时候目标函数的几何意义不明显或较复杂,函数方法适用情况更广些,同样保持题源的条件,问题改成了变式2.
第二天的作业即检测卷,笔者继续尝试,在全班范围内流水批改,每个小组负责批改本组出的题,在批改过程中既能看到其他同学对本组所出题目的疑问与评价意见,也能补充完善不同的解法.比如对于变式2,该小组批改后综合同学的做法,给出了较完整的解答过程:
除了解答,对他组题目的思考,也促进了同学们对问题不同层次的探索,比如对于变式2,有的小组发现如果目标函数关于某个变量单调,最值点就在边界上,只需将边界曲线方程代入目标函数即可转化成单变量函数的最值问题,于是将问题修改成关于两个变量均不单调:
随着变式的展开,问题慢慢演变为探究性作业了.此时笔者抓住时机肯定表扬了该小组,鼓励有兴趣的学生继续探讨解决这个问题,并将该题加入班级的“数学周报”,在积极性调动下,同学们经过思考交流,给出了以下解答:
回顾这样一次作业设计,笔者总结了几点体会:(1)选题或改编题促进学生进行题后反思,同时题后反思也在选改编题的过程中得到加强,这样的作业设计用于易错题或典型例题有较强的针对性;(2)尽管同一题源,各小组的选题自主、开放,不同于以往统一的作业形式,而是更加灵活多样;(3)将各小组的题目重新组卷、交换批改,这样的二次交流容易调动学生的积极性;(4)对题目或解答的优化完善过程往往充满了探究性,符合了不同层次学生的认知要求.当然,这样的作业设计需要解决的问题也很多,需要教师从整体上把握,但从中我们更深刻地体会到作业设计对课堂教学的重要性,充分调动学生积极性的作业设计是课堂教学的有效反馈和延伸,在今后的实践中需要继续做更多的探索.



作为课堂教学的反馈和延伸,作业设计是教学环节的一个重要组成部分,提高作业设计的针对性、层次性、创新性是提高教学实效性的重要环节.目前作业形式较广泛使用的是学校根据学情编写的导学案、校本作业等,笔者在实践中探索并尝试了由学生自主命题、解答、批改的开放式作业设计,
题后反思是纠错、总结、提升的有效途径,而这些反思心得往往需要及时地回到实际问题中通过练习进一步检验和巩固,这一后续环节通常我们会为学生设计好题组或变式.笔者在某次习题课的作业设计中尝试让学生以例题为题源,通过整理做过的同类题、查阅教辅教参或者自行改编等方式,生成一道检测题或变式题,收获了意外的惊喜,
解析方法1目标函数的几何意义(略);
方法2转化为单变量函数(略);
小结(生1)目标函数非线性时,最值点不一定在平面区域的顶点;
(生2)若目标函数具有较明显的几何意义,可以通过数形结合的方法求出最值点;
(生3)若目标函数的几何意義不明显,可以从函数的角度,转化为单变量函数.
各学习小组由该题源出发选题甚至改题、编题,提交的当日作业形成了一个题组.笔者将其中质量较高的题组成一份检测卷作为第二天的作业,如:其中一个小组将题源条件保持不变,问题稍加修改成以下的变式l,并分别给出两种方法的解答过程;另一小组则认为,虽然目标函数的几何意义可以从图形快捷地得到最值点,但更多时候目标函数的几何意义不明显或较复杂,函数方法适用情况更广些,同样保持题源的条件,问题改成了变式2.
第二天的作业即检测卷,笔者继续尝试,在全班范围内流水批改,每个小组负责批改本组出的题,在批改过程中既能看到其他同学对本组所出题目的疑问与评价意见,也能补充完善不同的解法.比如对于变式2,该小组批改后综合同学的做法,给出了较完整的解答过程:
除了解答,对他组题目的思考,也促进了同学们对问题不同层次的探索,比如对于变式2,有的小组发现如果目标函数关于某个变量单调,最值点就在边界上,只需将边界曲线方程代入目标函数即可转化成单变量函数的最值问题,于是将问题修改成关于两个变量均不单调:
随着变式的展开,问题慢慢演变为探究性作业了.此时笔者抓住时机肯定表扬了该小组,鼓励有兴趣的学生继续探讨解决这个问题,并将该题加入班级的“数学周报”,在积极性调动下,同学们经过思考交流,给出了以下解答:
回顾这样一次作业设计,笔者总结了几点体会:(1)选题或改编题促进学生进行题后反思,同时题后反思也在选改编题的过程中得到加强,这样的作业设计用于易错题或典型例题有较强的针对性;(2)尽管同一题源,各小组的选题自主、开放,不同于以往统一的作业形式,而是更加灵活多样;(3)将各小组的题目重新组卷、交换批改,这样的二次交流容易调动学生的积极性;(4)对题目或解答的优化完善过程往往充满了探究性,符合了不同层次学生的认知要求.当然,这样的作业设计需要解决的问题也很多,需要教师从整体上把握,但从中我们更深刻地体会到作业设计对课堂教学的重要性,充分调动学生积极性的作业设计是课堂教学的有效反馈和延伸,在今后的实践中需要继续做更多的探索.

