勾股定理教学中的核心素养培育

    徐萍

    

    [摘 ?要] 在初中数学教学中，要建立对核心素养的准确理解，应当结合具体的教学初中来进行. 勾股定理是初中数学中的重要知识点，也是充满探究意味的学习过程. 在这样的过程中，可以发掘到核心素养培育的多个元素. 站在学生的角度来看，学生经历了从生活事物到数学对象的转变，经历了在生活事物中发现数学规律，并通过数学运算、数据分析、逻辑推理得出这个数学规律的数学表达，于是就真正实现了用数学语言去描述数学规律的教学目标. 学生看到直角三角形后的第一反应往往就是勾股定理，这就是数学学科核心素养的表现.

    [关键词] 初中数学;勾股定理;核心素养

    在当前比较热门的核心素养的讨论语境当中，笔者感觉作为初中数学教师，需要清醒地认识到：核心素养的概念提出，固然是教育教学的一大进步，其具体到数学学科的六个要素（数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析）的表述，更加是为数学教学指明了目标;同时应当注意到的是，核心素养的培育不应当是一个空洞的过程，任何离开了数学知识学习与运用过程的教学目标，都是无法达成的，核心素养也不可能例外. 基于这一认识，笔者以为在初中数学教学中，要建立对核心素养的准确理解，还应当结合具体的教学来进行.

    勾股定理是初中数学中的重要知识点，也是充满探究意味的学习过程，在这样的过程中，可以发掘到核心素养培育的多个元素. 反之，如果从核心素养的角度去审视勾股定理的教学，并将这些环节明晰化，那么对核心素养的培育也是非常有帮助的. 本文就以勾股定理为例，谈谈笔者的相关思考.

    核心素养的培育需要基于知识教学

    强调核心素养的培育需要基于数学知识的教学，主要是从数学学科核心素养的六个要素来看，其都必须依靠具体的知识教学过程而进行，而初中数学因其知识内容相对较为抽象，核心素养的培养更加需要采取科学、合理的教学方式. 那么，基于知识教学的核心素养培育，还需要建立什么样的理解呢？笔者在分析了相关的理论研究成果与自身的实践案例的基础上，提出了如下几点认识：

    一是数学学科核心素养与数学知识之间是“神”“形”关系. 这个判断其实很容易理解，以数学抽象为例，数学抽象的对象是什么？是对生活事物、事例的抽象;数学抽象的目标是什么？是凸显生活事物、事例中的数学元素，并且用数学语言来描述;数学抽象的方法是什么？是包括分析与综合，是归纳，是逻辑推理等;数学抽象的结果是什么？是建立数学研究对象（常常以数学模型的形式存在）.

    在“勾股定理”的教学中，教学常常以毕达哥拉斯研究生活中的实例来创设情境. 当学生进入这个情境后，首先思考的是实例中的内容，在思考的过程中，会将实例抽象成图形，然后去寻求其中的数量关系（这也就实现了数形结合）. 通过这样的分析就可以看出，这样的一个学习过程中，学生的思维就已经经历了数学抽象、逻辑推理等过程，相应的这两个核心素养就可以得到培养.

    二是在数学知识生成的过程中建立核心素养视角，是核心素养落地的重要保证. 笔者在教学分析的过程中，有一个观点越来越清晰，那就是在核心素养提出之前，数学教学中并非不存在核心素养培育的环节，只不过在那样的教学情境中，核心素养可能被其他概念进行表述，也有可能是没有被教师和学生认识到，但其应当是存在的，否则就无法说明为什么传统的数学教学同样培养出了那么多优秀的人才. 但这种隐性的存在，对于教学来说最大的不足，就是不能将核心素养更加显著地凸显出来，因而也就不能针对核心素养的落地进行有针对性的教学. 因此在初中数学教学中，将核心素养作为教学及其研究的视角，让核心素养培育变得更加显性化，就可以保证核心素养的落地.

    “勾股定理”教学中培育核心素养的分析

    笔者在“勾股定理”的教学中，尝试以核心素养的视角去设计并实施，取得了较好的教学效果. 当然，这个过程中有对他人研究成果的借鉴，比如说有同行提出在“勾股定理”的教学中，通过创设教学情境，设计系列问题，引导学生探索、发现勾股定理，并引导学生从特殊到一般，用度量、数格子、拼图等多种方法验证、证明勾股定理，这样就可以让学生经历勾股定理建构的过程. 而且在这一过程中，可以让学生更积极地思考、尝试、探索，以一个创造者的身份探究知识，激发学生的学习热情，这样就可以发展学生的数学学科核心素养. 笔者在教学中，对其中的这样几个环节重点进行了引导：

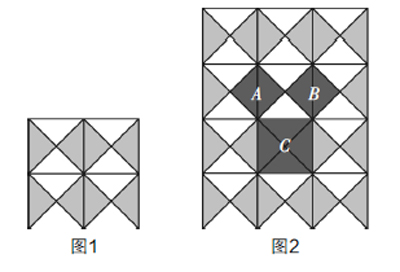
    在创设情境环节，笔者用现代教学手段向学生展示如图1所示的地面砖，然后用颜色凸显出其中的关键图形，如图2. 在这个过程中，学生对图1的观察，对图2的分析，其实就是一个数学抽象的过程，因为图1是实物，而图2是数学，从实物到数学，就是数学抽象的基本体现.

    在探究的环节：其后，笔者引导学生对A，B，C三个图形进行分析，尤其是从面积关系的角度进行分析，其实就是在数形结合的基础上，通过逻辑推理、数学运算、数据分析等，去发现数量关系（面积关系）. 当学生基于这个图形得出a2+b2=c2时，还有两个重要的核心素养培育的契机：一个就是对于其他普通的直角三角形，这个结论是否成立，这是从特殊到一般的演绎，而演绎原本就是思想方法之一，也是逻辑推理的体现之一;另一个就是证明勾股定理的新的方法的探究，因为勾股定理的证明方法非常多，适当地介绍或者是让学生探究新的证明方法，对于拓展初中学生的思维是非常有好处的，这是可以提升学生的数学学习品质的，因此是核心素养培育的空间之一，即使学生不能自主想出证明方法，教师向学生介绍“赵爽弦图”之类的数学史料，对于学生的数学思维拓展来说，也是非常有益的.

    在这样的教学过程中，可以发现数学抽象、逻辑推理、数学运算、数据分析非常丰富. 而当勾股定理的表达式最终出现并确认为定理时，其实际上又成为学生分析直角三角形的工具，是以模型的形态存在的，是数学建模的体现. 除此之外，在上述教学过程中，还应当结合数学实验来进行教学，因为数学实验能够促进学生的数学体验. 事实证明，将实验巧妙地与数学探究相结合，可以极大地激发学生学习数学的兴趣，通过学生主动参与实践过程，有利于深入探究解决问题，明确数学知识的来源、发展和应用，形成数学知识体系的核心素养.

    站在学生的角度来看，通过上述教学过程的参与，学生经历了从生活事物到数学对象的转变，经历了在生活事物中发现数学规律，并通过数学运算、数据分析、逻辑推理去得出了这个数学规律的数学表达，于是就真正实现了用数学语言去描述数学规律的教学目标. 从此以后，学生看到直角三角形，往往第一反应就是勾股定理所描述的关系，这显然是数学学科核心素养的表现. 即使从更为宏观的核心素养的角度来看，在这样的过程中，学生也更容易形成关键能力，且数学史的加入与数学探究的经历，对于培养学生的必备品格也多有帮助.

    初中数学教学中培育核心素养的分析

    勾股定理只是研究中的案例之一，当然也是较为成功的案例之一. 通过勾股定理的教学，来思考初中数学教学中核心素养的培育，笔者以为关键在于数学教学传统与数学学科核心素养的衔接. 也就是说，只有真正发掘传统教学中的核心素养培育因子，然后对其进行研究与表达，这样才可以让数学教师在教学中形成更加清晰的核心素养培育意识.

    这一点其实非常关键，因为只有教师自身具有了核心素养培育的意识，那么在实际教学中才有可能捕捉到核心素养培育的时机，学生也才有可能经历核心素养培育的過程. 特别需要指出的是，在数学学科核心素养的六个要素中，对学生来说最直接、最重要的可能应当是逻辑推理. 在勾股定理的教学中可以发现，正是逻辑推理衔接了前面的数学抽象与后面的数学建模，正是逻辑推理使得学生有进行数学运算与数据分析的空间，因此逻辑推理常常是打开数学学科核心素养培育的钥匙. 而且，逻辑推理其实可以向演绎推理与合情推理延伸. 众所周知，演绎推理和合情推理是数学核心素养下推理的重要组成部分，合情推理用于发现结论，培养学生的创新意识，演绎推理用于证明结论，培养学生严谨的分析问题、解决问题的能力. 显然，推理的过程也是推动核心素养落地的重要动力.

    由此也可以认为，在包括勾股定理在内的初中数学教学中，核心素养的培育与数学知识的教学，应当成为数学课堂上的两条主线，这两条主线互相影响、互相促进，两者之间的螺旋交替、螺旋上升的关系，实际上就印证了学生的核心素养落地的一个个步骤. 如此，核心素养落地自然也就有了空间.