思维的“种芽枝树花果”
李宾 周露
[摘 ?要] 中国学生的核心素养以培养“全面发展的人”为核心,其中表现之一是学会学习,因此对于数学学习更应该以培养学生学会思考,发展学生的思考力为目标. 文章以一节“平行四边形”习题课为例,发现通过课本一道习题的不断变式,起于课本、变于课本、生长于课本、发展于课本,对学生思考力的发展有很大的提升.
[关键词] 中国学生;核心素养;核心竞争力;思考力
教科书编者在编写教材时,会根据学生年龄结构的特征及学生对现有知识的储备,将知识点按照由浅入深、由易到难、由简单到复杂的螺旋上升的形式呈现. 因此,抓住教材中的典型习题,深入思考、适度变式探究,对调动学生的学习积极性、培养学生的思维品质、提高学生的数学素养具有重要的作用,同时教师的专业素养也能得到发展.
以一节“平行四边形”的习题课为例,对于一节几何习题课的教学,作为教师不能就题解题,应该关注所选的题型要巩固所学知识,更应该关注学生思维的生长. 笔者在本节教学中发现题型的不断演变对学生思考力的培养和提升有很大的作用.
播下思维的“种”——原型题
“思维的种子”指数学中的基本知识点、基本模型、基本问题,或是指一个问题的基本细节、部分或步骤等;换言之,“种子”指基本知识点或问题起始点,它是问题的根.
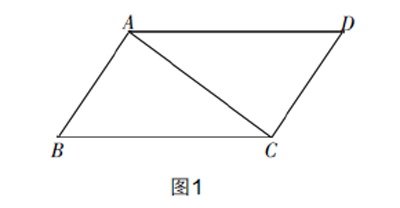
已知:AB=DC,AD=BC.
求证:△ABC≌△CDA.
本题是课本的一道基础题,是学生思维的起点,是对全等三角形判定的考察,绝大部分的学生对这个证明是没有问题的,设置本题的目的一方面是要调动学生的积极性与自信心,另一方面是提出基本问题为后面的探究做铺垫,从效果上来看还是非常好的,每一位学生都能积极参与进来.
发出思维的“芽”——变结论
“思维的芽”指在数学基本问题的基础上进行演变发展,问题有层次,但跳跃性不大,学生能够够得着,容易想到,学生的思维正以小坡度慢慢生长.
已知:AB=DC,AD=BC.
求证:AB∥DC,AD∥BC.
本题在前一题的基础上变了结论,条件没有变;结论在原有的基础上再递进了一步,培养学生在解决几何问题时不仅仅证出结论即可,而是要让学生养成一种思考的习惯,“在这个结论的基础上我还能够得到哪些新的结论?”“如果将条件再变一个还会有哪些新的结论?”长期通过这种生长性学习,学生很容易想到由“全等”得到“角等”,进而得出“线平行”. 通过习题的改编发展学生的思考力,问题的层层推进,同时又保持适当的距离,学生既不能轻易得手,又不觉得无计可施,使探究更具操作性. 数学的学习应该是以思维活动为核心的学习,在数学教学过程中,教师的重要任务就是培养和激发学生的探究欲望,寻求问题的发展和解决的过程.
抽出思维的“枝”——变图(课本P24,练习2)
“思维的枝”是指问题各部分或相关联问题之间的功能、作用及其相互关系等,它是一种联系,一种内在思维的脉络.
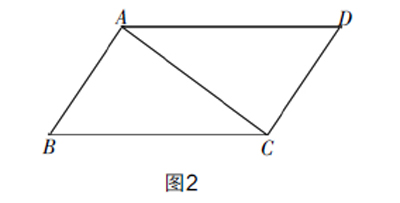
已知:AB=DC,AD=BC.
求证:AB∥DC,AD∥BC.
本题是在上一题的基础上进行了“变图”生长至课本P24的练习2,目的在于培养学生的构图能力. 从目标结论出发,要证“线平行”就要找“角相等”,从而想到全等,再来构造出两个三角形. 有了前面两题的铺垫,学生很容易想到作辅助线“连接AC”(或者“连接BD”),将本问题转化成上一个问题来解决. 本题通过变图发展学生的归纳思维能力,帮助学生的视角由整体走向局部,能够对图形进行分析和思考,提升学生的思维水平.
长出思维的“树”——逆命题考察(补充习题P08,题1)
“思维的树”指通过由浅入深、由易到难、由简单到复杂、由正向到逆向不断地以螺旋上升的方式呈现出来的完整的思维结构;问题的纵向设计与拓展,横向关联与变式,可以将简单问题延伸拓展作為复杂问题的基础,也可将复杂问题进行分解或转化为基本的、一些部分或步骤来分析与解决,进而形成思维的正向与逆向双向关联.
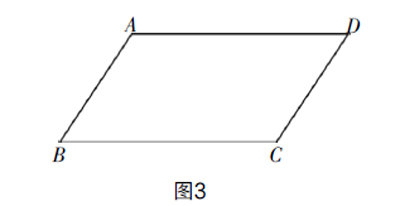
已知:AB∥DC,AD∥BC.
求证:AB=DC,AD=BC.
条件与结论互换,建立原命题的逆命题,是几何教学中最为常见的一种变式方法. 本题是上一个命题的逆命题,在前三个问题的基础上,学生容易想到做辅助线“连接AC”将图形分割成两个三角形,由“线平行”得到“角相等”,从而证明出三角形全等,得到“对应边相等”;此外,还会有部分学生是从目标结论出发,分析推理问题,在上一个问题的基础上学生逆向思考,要证“线相等”,只要证“三角形全等”,从而找“角等”,最后回到已知条件“线平行”上. 本题通过逆命题培养学生的逆向思维能力,不仅对提高解题能力有帮助,而且可以改善学生的思维方式,激发学生的创新精神,培养良好的思维品性,促进学生思维完整.
开出思维的“花”(课本P18,例4)
“思维的花果”指以教材习题为依托,将其往纵向挖掘,往横向延展,对相关内容进行整合、变形、变式、引申、拓展,把思维提升至学生的最近发展区,活化思维.
已知:△ABC,D是BC的中点,DE∥AC,DF∥AB.
求证:BE=DF,DE=CF.
本题看似与前几题图形有较大的不同,但通过前面几题画图、描图、作标记、析图的过程,学生的头脑里已经初步建立了模型,能够从较复杂的图形中剥离出基本图形. 由上一题生长至课本18页的例题,巩固学生的思维成果. 从课堂效果来看,通过前面几题的铺垫和变式,绝大部分学生都能够掌握了. 从基本图形出发逐渐改变图形,让学生清晰地了解图形的基本要素之间的关系,然后逐渐拓展延伸基本图形,使学生的思维更具有灵活性.
结出思维的“果”
前一题的结论证明出来后,在这个基础上让学生继续思考还能得出哪些结论. 以下面的变式1为例,引导学生的思维到达“三角形中位线”的最近发展区.
变式1:求证:E,F分别是AB,AC的中点.
在前一题的基础上学生已经得出BE=DF,DE=CF,要证E,F分别是AB,AC的中点,只要证AE=DF,DE=AF即可,这时就会发现只要将图①、图②遮住,这个问题其实就是第三题的原题. 通过大半节课的学习,原图的思维种子已经在学生的头脑里生根、发芽、成枝了,再通过读题、描图、作标记,学生很快就会发现这个图中隐藏的平行四边形,问题就迎刃而解了. 接下来的探究问题不再是给定的了,而是放手让学生自主去挖掘探究,让不同的学生都能以探究者的姿态出现,去体验创造成功的感受,定能让学生的思维得到锤炼,创造性思维得到发展. 从课堂效果来看,学生的思维已经达到高潮,非常的活跃.
“连接EF”后这个图形被分成了四个小三角形,由前面的证明已经知道①和②是全等的,③和④是全等的,大部分学生立即猜想这四个小三角形是否都全等?学生通过演绎推理能够轻松地证明四个三角形全等,视角已经能够由局部走向整体. 在这样的探究劲头下,有学生发现EF∥BC,这时教师适当加以追问“EF在位置上是平行于BC,在数量上是什么关系呢?其他两条线段DE,DF也有同样的发现吗?”虽然没有给出定义,但这时学生的思维层次已经达到了解三角形中位线的水平了. 此外,还有四个小三角形的周长、面积与大三角形的周长和面积之间的关系,学生都能够发现并说理出来. 虽然下课铃已经响起来了,但学生探究的热情并没有结束,一节好课的最高境界不是“我会了”,而是“我还想学”.
整节课教学思路清晰,由课本的一道原题,通过“低起点、小坡度、有高度”不断变式、拓展将学生的思维提升至三角形中位线的水平,甚至“生长”到九下相似三角形的性质的位置;几个变式图成系统,有主线,每一个题目的过渡自然流畅,符合学生的认知规律和思维水平;内容上丰富多样,涵盖课本、补充习题上的所有同类型的题目. 在整节课中通过描图、作标记、析图的过程培养学生抽象建模的能力,通过“一题多变”促进学生的数学思维能力、演绎推理能力和口头表达能力的提高. 在教学中应关注学生发现问题、提出问题、分析问题、解决问题的能力,关注思维的方向性、层次性、灵活性、品质性,才能优化学生主动建构知识的过程,提升思考力,激发智慧.
《义务教育数学课程标准》指出:数学知识的教学,要注重知识的“生长点”与“延伸点”,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解.
思考力的提升是一个积累的过程,要想学好数学,要想成为一个独立思考的人,思维训练必不可少,尤其对于几何这部分的教学,更需要借助對题型的不断演变,发展学生的思维. 题型的演变必须以“低起点、小坡度、上高度”为主线,让不同水平的学生都能得到一定的发展. 因此教师在数学教学过程中要把发展学生思考力作为重要的目标,借助典型的问题,引导学生运用已有的知识经验,将不熟悉的问题与熟悉的问题进行类比;在教学设计时善于将教学内容“生长”下去,促进学生新、旧经验的相互作用丰富或调整原有的认知结构,顺利进行知识建构. 使学生能不仅更系统的、完整的掌握数学知识,更为数学思维的发展打下坚实的基础.

