模型思想，发现图形的美

    李维

    

    

    

    [摘? 要] 模型思想是初中数学学习的重要思想之一，在数学课堂教学中，数学思想的渗透与感悟是践行学生核心素养落地生根的关键. 教师需要将思想镶嵌到情境中，启发学生发现情境中的数学问题，并将问题转化成数学模型，从而通过模型思想和数学工具一一突破问题. 教师要让学生在长期的学习与应用之中，提升对模型思想的感悟与应用，将思想转变成一种应用能力与一种学习习惯.

    [关键词] 模型思想;图形;初中数学;能力;素养

    数学模型就是用数学语言和数学符号所构建的科学模型，模型思想就是构建数学模型的思想. 在数学学习中，模型思想是一种重要的思想，也是一种常用的方法，更是一种实用的工具，尤其在解决问题的过程中，有着不可替代的作用. 简言之，模型思想就是在解决问题时，根据问题所提供的信息及其特征，抽象出数学基本模型，从而使问题由繁化简、由难化易. 对于初中数学而言，模型思想在几何问题解决中的重要作用尤为突出，下面结合初三一轮复习专题“线段和的最值”（苏科版），谈谈笔者的感悟.

    模型1：“将军饮马”模型

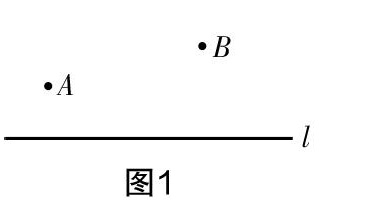
    将军饮马模型是路径最短问题中的经典模型，抽象成几何模型即为：如图1，点A，B是直线l同一侧的两个点，在直线l上求一点P，使AP+BP的值最小.

    利用轴对称的性质，作点A关于直线l的对称点A′（如图2），则AP的长度可以转化为A′P的长度. 利用“两点之间，线段最短”，可知当A′，P，B三点共线时，AP+BP的值最小.

    例1如图3，在∠AOB的内部有一点P，分别在OA，OB上各找一点M，N，使△PMN的周长最小.

    分析上述问题显然和“将军饮马”的“两定一动”模型有所区别，此题属于“一定两动”，但思路却是相通的. 如图4，分别作点P关于直线OA，OB的对称点P′，P″，则MP可以转化成MP′，NP可以转化成NP″，△PMN的周长即为P′M+MN+NP″. 连接P′P″，依据“两点之间，线段最短”，即可找到M，N的确切位置，使△PMN的周长最小.

    例2如图5，∠AOB的边OA，OB上分别有点M，N，且OM=1，ON=3，P，Q分别是OB，OA上的动点，已知∠AOB=30°，试求MP+PQ+QN的最小值.

    分析该问题属于“两定两动”问题. 根据将军饮马模型的思路，只需作M关于直线OB的对称点M′，N关于直线OA的对称点N′（如图6），则MP+PQ+QN=M′P+PQ+QN′. 连接M′N′，则M′N′的长度即为MP+PQ+QN的最小值. 易证∠N′OM′=90°，由对称的性质知OM′=OM=1，ON′=ON=3，所以M′N′=.

    “两点之间，线段最短”是将军饮马模型的依据，几何图形中能够快速发现该模型的方法就是找点，通常具备“两定一动”“两动一定”和“三动”特征的点时，即可利用该模型来求解.

    模型2：垂线段最短

    “直线外一点到直线上所有点的连线中，垂线段最短”是基本定理，将此定理运用于几何图形中，即可成为一个解决线段之和最短问题的基本几何模型.

    例3如图7，∠AOB的边OB上有一定点C，在OA，OB上分别求一点M，N，使CM+MN的值最小.

    分析首先利用轴对称作点C关于直线OA对称的点C′（如图8），则CM即可转化为C′M. 当C′，M，N三点在同一条直线上时，CM+MN有最小值，即C′N的长. 由于点N不固定，所以线段C′N的长度也在不断地发生变化，但当C′N⊥OB时，线段C′N的长度最小，此时正是CM+MN的最小值.

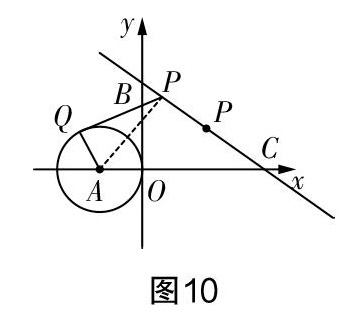
    例4如图9，在平面直角坐标系中，☉A的半径为1，圆心A的坐标为（-1，0），点P为直线y=-x+3上的一个动点，过点P作☉A的切线，切点为Q，在点P运动的过程中，切线PQ的长度也在不断变化，这个长度是否存在最小值？請说明理由.

    分析根据切线长的计算公式，无论点P在何位置，PQ=总成立. 由图10可知，点P运动时，☉A的半径不变，所以当PA取得最小值时，PQ也取得最小值. 依据“垂线段最短”可知，当AP⊥BC时，PA的长度最小，此时切线PQ的长度也最小. 要求此时PQ的长，可以先证△COB≌△CPA，从而得到PA=OB=3. 再利用勾股定理，即可求出PQ==2.

    针对动态问题，“动中求静”是一种策略. 在上述模型中，“动”中的“定”通常是一个定点，找准定点后利用对称的方法将线段之和转化成一条线段，再根据“线段最短”，即可解决问题.

    模型3：圆上的最近点（最远点）

    如图11，点P是☉O外一点，A，O，B，P四点共线，则点P与圆上所有点的连线段中，PA最长，PB最短. 当点P是☉O内一点时，结论依然成立（如图12，当然，此时点P离点B更近一些）.

    例5如图13，在边长为4的正方形ABCD的边AD上任取一点E，连接BE，过点A作BE的垂线，垂足为F，点P是AD边上另一动点，连接PF，PC，求PC+PF的最小值.

    分析由AF⊥BF可知点F的运动轨迹为以AB为直径的半圆弧. 在正方形ABCD的左边作一个与之全等的正方形AB′C′D，连接PC′，则PC=PC′，PC+PF=PC′+PF. 所以当C′，P，F三点共线时，PC+PF取得最小值. 于是问题转化成当点F在什么位置时，C′F的值最小. 由上述模型可知，连接C′O（其中O为AB的中点），其与半圆弧的交点即为所求的点F. 利用C′F=CO-FO可以求出此时C′F的长.

    因为圆上的最近点和最远点都与圆有关，所以在问题中发现“隐圆”非常重要，而该圆通常是点的轨迹. 所以，当几何问题中出现圆时，可以考虑利用这一模型来求解.

    模型4：三角形

    “两边之和大于第三边”是三角形的三边关系，从另外一个角度可以描述为“三角形的一条边小于另外两条边之和”，这便可以成为线段和最值问题的一个几何模型.

    例6如图15，△ABC为等腰直角三角形，∠ACB=90°，AC=BC=4，D为线段AC上任意一点，连接BD，过点C作BD的垂线，垂足为H，连接AH，求AH的最小值.

    分析题中无法直接看出何时AH的值最小，根据所给条件“CH⊥BD”可知△CBH为直角三角形，如图16，取BC的中点G，连接HG可知HG为直角三角形CBH斜边上的中线，因此HG=BC为定值. 若AH取得最小值，则AH+HG取得最小值. 连接AG，得到三角形AGH，根据AG

    例7如图17，☉O是半径为1的圆，MN是它的直径，点A是圆上一点，且∠AMN=30°. 已知=，P是直径MN上的一个动点，求PA+PB的最小值.

    分析图中A，B为定点，可以作点B关于直线MN对称的点B′，则PA+PB=PA+PB′. A，P，B′可以构成一个三角形模型，根据“两边之和大于第三边”可以判定，当A，P，B′三点共线时，PA+PB的值最小，于是可确定点P的位置. 计算PA+PB的最小值，就是计算AB′的长. 根据同弧所对的圆心角与圆周角的关系可知∠AON=2∠M=60°，由对称可知∠B′ON=∠BON=∠AON=30°，所以△AOB′为等腰直角三角形，AB′=. 所以PA+PB的最小值为.

    “两边之和大于第三边”模型与“将军饮马”模型有相通之处，它们的实质都是“两点之间，线段最短”，同时它们也存在细微的区别. “将军饮马”模型突出对称，而“两边之和大于第三边”中三角形的存在较为明显. 解决问题时，应仔细观察图中隐含的图形，或构造目标模型，或找到三角形运用“两边之和大于第三边”模型来解决问题.

    灵活、多变是数学问题的特征，“变”让几何图形千姿百态. 正是这些“变幻莫测”的几何图形，有时让学生觉得难以突破. 诚然，几何图形的变化有规律也有依据，这个依据便是基本几何模型，所以挖掘条件，分解图形，找到复杂图形中隐含的几何模型，是解决几何问题的基本思路. 对于教师而言，在教学中应渗透模型思想，力争让学生发现图形的美，发现数学的美，攻克数学问题，从而爱上数学.