对一道抛物线综合题的思路突破与思考
罗晓峰
[摘? 要] 以抛物线为载体考查学生信息提取和转化的能力、数学模型构建能力的综合类考题成为近几年中考的压轴题之一. 该类考题一般涉及众多的知识点,问题类型多样,如基本点和函数解析式的求解,以及复杂度较高的存在性问题,前者只需要考生按照基本的解题步骤解决即可,而后者就需要對问题结构有充分的认识. 文章对一道抛物线综合题展开思路探析与解后思考,并提出相应的教学建议供读者参考.
[关键词] 抛物线;存在性;定理;转化;模型
考题呈现
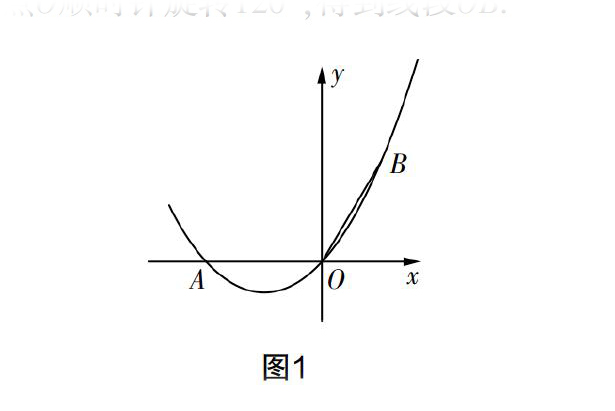
试题 如图1,在平面直角坐标系中,点A的坐标为(-2,0),线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标.
(2)若某抛物线的图像经过A,B,O三点,试求该抛物线的解析式.
(3)(2)问所求的抛物线的对称轴上是否存在一点C,使得以B,O,C为顶点的△BOC的周长最小?如果存在,请求出此时点C的坐标;如果不存在,请说明理由.
(4)若点P是(2)问所求抛物线上一个动点,且该点位于x轴下方,试分析以P,A,B为顶点的△PAB的面积是否存在最大值. 如果存在,请求出此时点P的坐标和△PAB的最大面积;如果不存在,请说明理由.
思路突破
1. 第一步:巧借性质,构建模型
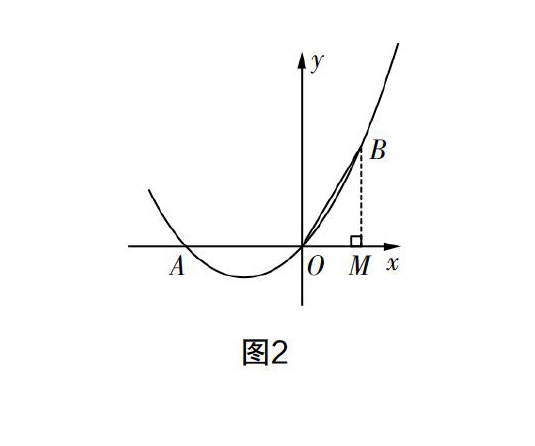
对于第(1)问,要求点B的坐标,首先要理解点B获得的过程. 考虑到OB是由线段OA绕点O顺时针旋转120°得到的,因此需要充分利用几何旋转的性质来构建相应的模型. 过点B作BM⊥x轴于点M,如图2,则求点B的坐标实际上就是求线段OM和BM的长. 由线段旋转的性质可知,OA=OB=2,又∠AOB=120°,所以∠BOM=60°. 在Rt△OBM中使用三角函数,得OM=OB·cos60°=1,BM=OB·sin60°=,所以点B的坐标为(1,).
2. 第二步:待定系数,常规求解
第(2)问求经过A,B,O三点的抛物线的解析式,一般需要将其设为y=ax2+bx+c(a≠0),其中a,b,c是抛物线的特征参数. 从方程角度思考,要求未知数a,b,c,需要构建相应的方程组,进一步分析,则需要得到抛物线上三个点的坐标. 已知该抛物线经过A,B,O三点,所以可以分别将其坐标代入. 将原点O的坐标代入解析式,可求得c=0,再将A,B两点的坐标代入解析式,可构建方程组4a-2b=0,
3. 第三步:问题转化,定理突破
第(3)问是在第(2)问的基础上进行的点存在性问题探讨,该问有两个关键条件需要处理:一是点C在抛物线的对称轴上,其横坐标必然为一定值,设点时应充分利用;二是要确保△BOC的周长最小,这需要构建相应的几何模型,将几何问题转化为相应的代数问题.
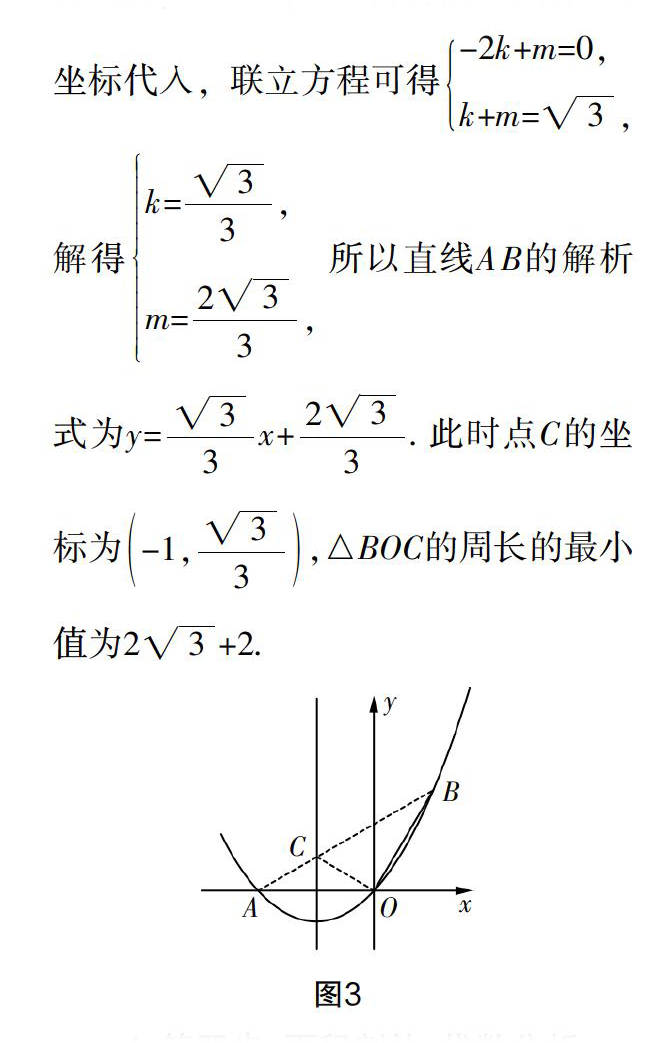
易求得抛物线的对称轴为直线x= -1,于是设点C的坐标为(-1,yC). 对于△BOC,边OB为定值,则要使△BOC的周长最小,就必须确保CO+CB的值最小,因此问题转化为求线段和的最小值. 对于该问,可以借助“两点之间,线段最短”的原理来求解,即在对称轴的另一侧构建与CO等长的线段. 已知点A和点O关于抛物线的对称轴对称,又点C在抛物线的对称轴上,所以OC=CA. 于是问题进一步转化为求BC+CA的最小值. 因此,当A,C,B三点在同一条直线上时(如图3),BC+CA取得最小值. 连接AB,AB与直线x=-1的交点就是满足条件的点C. 设线段AB所在的直线的解析式为y=kx+m(k≠0),将点A和点B的坐标代入,联立方程可得-2k+m=0,
4. 第四步:面积割补,代数分析
第(4)问的点P为抛物线上一个动点,分析△PAB的面积是否存在最大值,首先需要设出点P的坐标,然后相应地构建△PAB的面积模型,将其转化为关于点P坐标参数的二次函数,然后通过研究二次函数的性质来分析面积的最值.
假设存在满足条件的点P. 根据题意,设点P的坐标为x,
解后反思
1. 关键步骤的分析
从问题类型来看,上述考题的第(3)(4)问均属于最值存在性问题,解题突破时,均存在几个关键步骤. 第(3)问求三角形周长的最小值,结合三角形的周长公式可知,该问题实际上就是求线段和的最小值,解题需要构建线段和的最小值模型,解题的关键一步就是基于几何定理分析线段的最小值. 而第(4)问分析三角形面积的最大值,以及对应的点P的坐标,对于该类问题,需要结合代数进行分析. 考虑到三角形为一般三角形,因此突破该问的关键步骤有两个:一是如何构建三角形的面积模型——割补法,二是如何分析最值问题——函数性质.
2. 存在性问题的策略
近几年的中考压轴题越发注重考查学生的综合思维,以动点为背景的存在性问题是其中的一类,该类考题一般为分析满足某种条件的情形是否存在,如上述求三角形的周长最小值和面积的最大值. 问题一般分为两类:一类是肯定性问题,另一类是否定性问题,本考题就属于肯定性问题. 对于肯定性问题,一般存在三种解题策略:一是直接由条件入手,逐层突破,试求满足条件的问题情形;二是假设结论存在,然后根据已知条件,结合数学公式、定理,构建相应的问题模型,采用推理演绎的方法加以论证;最后一种则是采用反证法,假设所要分析的对象不存在,然后对其加以否定淘汰,从而证明结论. 上述三种方法并不是完全独立的,有时也可以结合起来综合推理,如上述考题第(4)问就采用首先假设动点存在,然后由条件出发构建面积模型,进而论证动点存在的方式. 因此,在后续解析动点存在性问题时,要充分利用已知条件,采用合理的解题策略来突破.
教学建议
1. 辨识考题,合理转化
以抛物线为载体的存在性考题是中考数学压轴题的典型问题之一,该类考题需采用合理的解题策略逐层剖析,合理转化,因此在审题阶段准确定位考题类型十分重要,其是后续解析、转化的基础. 在教学中,教师要注重引导学生掌握考题辨识的方法,按照“条件解读→图形绘制→问题分析”的步骤来充分认识考题,尤其要在对条件和问题的辨识过程中引导学生仔细提取其中的关键词,从中提炼出具有鲜明代表的词汇,如“是否”“存在”“若”等. 一般存在性考题的综合性很强,需要对问题进行充分转化,如上述利用数学公式转换几何周长、面积,利用割补的方法转化面积等,因此在教学中要引导学生强化基础知识,充分理解数学的公式、定理,并灵活运用,从而帮助学生获得破题的方向和转化的方法.
2. 善构图形,充分思考
抛物线存在性问题的一个典型特点是考题一般与图形紧密联系,这是因为利用图形不仅可以直观地呈现考题条件,还可以通过图形的阅读来考查学生的读图能力. 而对于考生来说,充分利用考题图像,构建相应的解题模型,则成为考题突破的重要环节,这也是该类综合题突破的难点所在. 在初中阶段,数形结合分析考题主要有三个角度:一是以数驭形,二是以形助数,三是数形互通. 在解题教学中,教师可以引导学生将其分为三个阶段:首先,充分读取题干条件,根据条件信息绘制相应的图像,然后结合图像进一步分析考题,充分挖掘其中的隐含信息,最后采用数形对照的方式来转化考题,构建相应的解题思路. 在上述解题过程中,学生的思考逻辑极为重要,要引导学生掌握利用图像信息进行思考推演的方法,掌握图像模型构建的基本策略.

