立足特征,把握联系,突破综合
王一欣
[摘? 要] 几何图形与函数相结合的综合题,一般题型结构复杂、注重知识联系、问题变化多样,以考查学生的综合能力为命题根本. 文章以一道几何与二次函数综合题为例,探析解题思路,分析解题策略,并提出相应的教学建议.
[关键词] 二次函数;平行四边形;性质;联系;综合题
问题的提出
近几年的中考命题逐渐向着知识综合的方向发展,以考查学生的综合能力,在中考压轴题中存在这样一类问题——几何图形与二次函数相综合,其中以基本图形最为普遍,如平行四边形与二次函数相综合. 对于该类问题的分析首先需要对平行四边形和二次函数的性质特征,以及两者之间的关联性有所了解,下面将对其进行深入探析.
性质特征的解读
在初中教材中将有一组对边平行且相等的四边形或两组对边分别平行的四边形称之为平行四边形,这是对平行四边形的基本定义. 对于该定义我们需要从如下角度进行理解,首先要明确平行四边形异于普通四边形的根本,即定义中的“平行”二字,需要满足两组对边均平行. 当满足上述条件后平行四边形的两组对边就存在相等的性质,即平行四边形的对边平行是其根本性质,而对边相等是其核心性质,在研究与平行四边形相关的题目时可以从上述两点进行.
考题的探究
中考中平行四边形与二次函数的综合题,除了考查图形特征和函数性质外,另一个重点是对两者关联性的考查,解题的关键也是把握联系,明晰结构,下面将对一道考题进行探究.
(2)分析是否可能存在由PA,PB,PC和PD构成平行四边形,需要从平行四边形的性质出发,一旦存在一条不满足平行四边形的条件即可证明不能构成. 考虑到题干给出的是线段长,则可以考虑从平行四边形的对边相等角度来分析. 根据问题可知需要分为点P位于正方形的EF和FG上两种情形:①当位于EF上时,连接PM,如图3所示,由于点E,F和B三点共线,而点C在y轴上,则PB
解后思考
1. 解题思路的反思
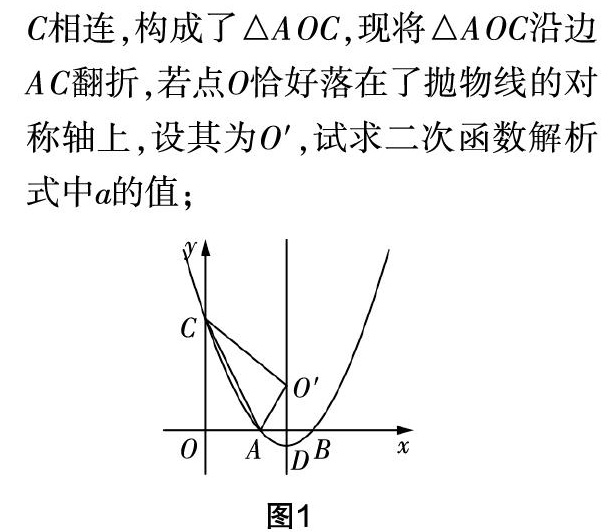
上述考题是二次函数与几何图形的综合题,第一问以图形翻折为背景,考查结合几何性质求解二次函数的解析式. 根据题干的文字叙述显然需要从图形翻折中分析线段长的几何关系,然后从点坐标与线段的联系性入手构建解析模型,进而确定求解参数a的关键点. 该问的关键在于敏锐发现直角三角形中线段的特殊关系,分析其内角,确定线段长,即直角三角形中30度角所对的边等于斜边的一半.
而考题的第二、三问均是分析平行四边形存在性,对于该问的求解需要从平行四边形的定义入手. 考虑到问题给出了线段的长,因此从边长角度来考虑更为简洁,上述无论是对比线段长,还是分析实数a是否存在都是基于该定义来开展的. 解题的关键均是利用图像中点坐标与线段长之间的关系,构建相应的分析模型,其中第三问构建的代数方程模型是该类问题常见的解法思路,是函数与几何综合题转化的重要策略.
2. 解题思想的反思
函数知识是几何与代数的综合,这也是中考常将二次函数与几何图形相结合命制考题的关键,因此分析该类问题最为关键的思想就是数形结合思想,即借助图像的直观性分析图形关系,然后基于图形关系采用代数分析的方式来精准求解. 该思想的使用有两个过程:一是利用题干的信息绘制相应的图像,二是分析图像中的圖形关系,并结合函数的性质特征转化为相应的代数问题,可以直观比较代数值的大小,也可以构建求解相关参数的代数方程,总之通过代数的运算分析来完成求解. 在实际解题中不仅需要懂得数形结合的思想内涵,还需要掌握数形结合思想运用的思路,领悟思想的精髓,内化为解题策略.
教学建议
1. 扎实学生基础,注重知识融合
几何图形与二次函数的综合题涉及平面几何与二次函数众多的知识点,该类问题求解的基础依然是对几何与函数两大模块知识内容有着充分的了解,能够灵活运用其中的知识内容求解基础问题. 如上述考题涉及求直角三角形的线段长、证明四边形为平行四边形、求函数解析式的顶点、交点和对称轴等. 因此在教学中需要教师充分利用数学教材,从基础内容出发,帮助学生扎实基础,然后在此基础上开展知识的融合教学,挖掘知识间的联系,帮助学生完善知识体系,为后续求解综合问题打下基础.
2. 掌握解题方法,形成解题策略
综合题求解的难点在于解题思路的构建,一般求解综合问题需要经历问题转化与拆分、关键条件探寻、条件与问题重构以及构建解题模型四个阶段. 思路构建的过程包括了对问题的思考、条件的分析、联系性构建和模型选取,对学生的思维要求较高. 因此在解题教学中,教师应该偏重解题思路的引导,使学生经历思维分析的各个阶段,充分感知问题的分析过程,必要时可以引导学生分析错解的原因,加深理解. 解一题,通类题,引导学生掌握解题的方法策略远比学解一道例题重要,提升学生解题的思维远比掌握考题的解法重要.

