分层走班是一道靓丽的风景线
丁同军


[摘? 要] 分层走班教学符合新课改的发展要求,体现了因材施教、以人为本的教学原则. 分层教学充分认识差异、尊重差异、研究差异,并针对不同层次的学生进行分层备课、分层教学、分层命题、分层作业、分层辅导……能真正提高课堂效率.
[关键词] 目标分层;教学分层;作业分层;辅导分层
古人云“孔子教人,各因其材”,指的是教学应从学生的个性特点出发,有的放矢地进行差异化教学,以使每个学生都能得到最佳发展[1]. 随着数学的难度逐渐增大,优生吃不饱、差生吃不了的问题日益突出,于是我们進行了分层走班教学初探.
基础扎实,学习能力突出的尖子生划为A班;基础一般,学习能力不突出的中等生划为B班;基础欠缺,学习能力较差的后进生划为C班. 对目标进行分层:A班除了完成“课标”规定的教学任务之外,还需在深度上挖掘,在广度上拓展,加强能力培养;B班要立足课本,夯实基础,注重知识、技能的训练;对于C班的教学,则要强化学法指导,培养学生的兴趣,树立学生的信心.
案例1? ? ?九年级数学“垂径定理”的目标分层设计.
从知识、技能、能力和思想方法等方面提出分层要求:A班学生在充分理解、掌握垂径定理的基础上,会灵活应用定理解决问题,让学生经历“实验—观察—猜想—验证—归纳”的研究过程,培养学生动手实践、观察分析、归纳问题和解决问题的能力,灌输勇于探索的精神;B班学生在理解、掌握垂径定理的基础上,灵活运用定理解决问题,通过圆的轴对称性探究圆的相关性质,进一步体会和理解研究几何图形的方法,培养学生实事求是的科学态度和积极主动的参与精神;C班学生理解勾股定理并基本掌握垂径定理,能应用垂径定理解决简单的问题,让学生动手、动口、动眼、动脑,培养学生的能力,激发学生的求知欲,让学生感受数学与生活的紧密联系.
课堂教学是分层教学的主阵地,是决定分层成败的关键. 教师应深入研究教材教法、学生学情,精心设计不同层次的课堂. A班的教学要少干涉多放手,让学生在独立探究和合作交流中学习;B班的教学则要紧扣基础,强化能力训练,培养良好的学习习惯;C班的教学需低起点、低要求,不违背规律,不揠苗助长.
案例2八年级数学“全等三角形的判定”教学分层设计.
C班按照“课标”要求分5个课时按部就班地教学. A班则把四个定理放在同一课时中呈现,利用问题“一块三角形玻璃摔成两块,带哪一块去配和原来一样的三角形玻璃”引出新课,诱导学生分析判断两个三角形全等的条件. 从三边三角的元素中选3个,其中有4种情况可以判定两个三角形全等,进而归纳出全等三角形的4个判定定理. 还要求A班学生能辨别“AAA”和“SSA”不一定能证明两个三角形全等. 最后通过2节习题课巩固、提高. 这样的设计,3节课就完成了5节课的任务,既提高了课堂效率,又增强了知识之间的联系. B班学生的水平介于A班和C班之间,教师可以根据需要把A班或C班的成功经验推广到B班教学中.
为了巩固和延续课堂教学效果,作业也要分层:基础性作业主要针对的是后进生,考查基本概念、公式、性质等,以巩固基础、培养习惯为目的;提高性作业主要针对的是中等生,以能力发展、拓展延伸类试题为主,训练解题素质;创新性作业主要针对的是优生,以中上难度题为主,培养综合思维能力.
分析题目:本题主要考查圆周角定理、勾股定理等知识.
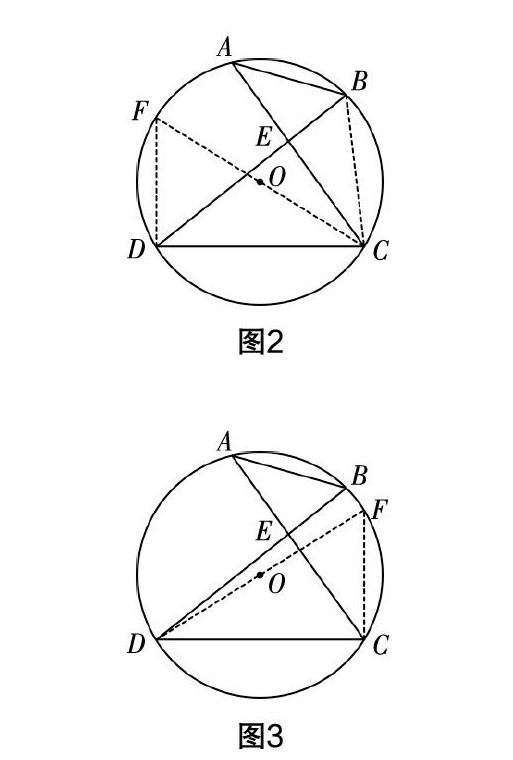
分层辅导:(1)对A班学生的辅导:A班学生的解题能力强,教师应放手让学生自主学习,并适当提示. 本题由问题引出,让学生探索辅助线的作法——如图2的CF或图3的DF,构造Rt△CDF. 图2由圆周角定理知∠F=∠DBC,再利用等角的余角相等得∠FCD =∠BCA,从而推出DF=AB=2. 同理,可得图3中的弦FC=AB=2,最后可用勾股定理求出直径.(2)对B班学生的辅导:对于B班的学生,教师应给予更多的帮助,应预设解题铺垫,让学生拾阶而上. 可运用分析法引导学生添加直径,如图2中的CF或图3中的DF,构造出Rt△CDF,再利用圆周角定理推出DF=AB=2(图2),最后用勾股定理算出直径. 如果时间允许,可让B班学生和A班学生一样,尝试添加图3中的辅助线来求解. (3)对C班学生的辅导:C班学生解这道题难度较大,需做到以下几点:①由易到难,先预先铺垫好本题相关的知识点,增设过渡学习的缓冲区;②循循善诱,切勿急于求成,可从添加辅助线的方法到圆周角定理推出弦长,最后通过勾股定理求出直径;③及时鼓励,要善于发现学生的闪光点并及时给予表扬;④题后小结,解题后要及时归纳方法,形成经验.
今后,我们将继续开展分层走班研究,不断地改进分层走班教学,让分层走班成为校园中一道靓丽的风景线.
参考文献:
[1]李庾南. 自学·议论·引导教学论[M]. 北京:人民教育出版社,2013(7).
[2]李庾南,陈育彬. 中学数学新课程教学设计30例——学力是这样发展的[M]. 北京:人民教育出版社,2007.

