用叠加模式将数学史融入数学教学
孙雨琴 朱哲

【摘 要】 ?数学史的融入方式直接影响着数学教学的质量.文章以“顺应——重构”叠加模式将数学史融入到数学教学中,以“导数的几何意义”为例设计一则教学案例,再从“整理史料、问题驱动、重构再现、反思升华”四个模块进行分析,从而得到一些启示,以期为数学史融入数学教学起到些许借鉴作用.
【关键词】 ?叠加模式;数学史;数学教学;导数的几何意义;教学设计
以HPM视角融入到教材设计和课堂教学,日益受到一线教育工作者的关注.2016年在德国汉堡大学举行的第十三届国际数学教育大会中第25个研究专题强调,要认识数学史在数学课堂和教学中的作用 [1].
根据汪晓勤教授的划分,数学史融入到数学教学的模式可分为以下四种:分别是附加式、复制式、顺应式和重构式.其中重构式指借鉴或重构知识发生、发展的历史,浓缩概念发展的过程,让学生经历概念的形成过程,其教学目的主要为加深对概念的纵向与横向的理解.其更注重的是将数学史知识融入在认知方面的作用.而顺应式主要指改编历史上的数学问题、方法,提炼其背后的数学思想,其教学目的主要是在教学过程中渗透重要的数学思想.两者虽各有所长,但彼此也都存在一些缺陷.比如,重构式难度较大,缺少直观性,易使课堂枯燥;而顺应式较浅显,不易挖掘出知识的内涵.现今,我国中学数学教材对于数学史的融入大都以单独的方式,如若将它们结合起来,在“顺应式”中融入“重构式”,显然会使教学更优化.因此,笔者将以“导数的几何意义”教学设计及分析为例来探讨“顺应——重构”叠加模式的运用.
1 切线概念的发展历史
通过数学史的简单介绍,笔者了解到切线概念的形成过程,是经历了由静态到动态的一个发展过程.古希腊数学家欧几里得最早定义了圆的切线,接着阿波罗与阿基米德用欧几里得的方法定义了圆锥曲线与螺线曲线,而那时在古代数学中,切线的定义还局限于静态的定义——与曲线只有一个公共点且位于曲线一侧(或“不穿过”曲线)的直线.
直到17世纪,数学家相继发现和研究了一般曲线的不同构造法.其中,巴罗利用“特征三角形”的概念——实质上把切线看作是割线的极限位置.而直到17世纪下叶,切线为割线之极限位置的思想才成为数学家的共识.德国数学家莱布尼茨将曲线的切线定义为“连接曲线上无限接近两点的直线”,或“曲线的内接无穷多边形的一条连续边” [2].法国数学家洛必达在其《无穷小分析》中亦将曲线的切线定义为曲线的内接“无穷多边形”一边的延长线 [3].
可见,切线定义从静态走向动态跨越了数千年的岁月,而了解切线的发展历史,有利于教师把握学生的认知起点,也为教学设计打开了新的视野.
2 学生的认知起点
学生对切线的认知起点是圆的切线,因而教师首先可以从圆出发,让学生回顾圆的切线的定义.圆的切线主要有3种定义方式,分别为:与圆只有一个公共点的直线;过圆上一点且垂直于该点与圆心连线的直线;到圆心的距离等于圆的半径的直线.其次,让学生反思,上述定义是否适用于圆锥曲线呢?显然不适用,以抛物线为例,对称轴与抛物线只有一个交点,但不是切线.学生很自然会对定义添加约束条件,得到“与曲线只有一个公共点且不穿过曲线的直线”.这就是古希腊数学家给出的适用于圆锥曲线的切线定义,但是适用于更为一般的曲线吗?反之,直线与三角函数y=sinx的图象有不止一个交点,它是曲线的切线吗?所以,切线概念的教学必须让学生认识到“是否只有一个公共点”也不是切线的判别标准,激发学生寻求新的切线定义,为形成“切线是割线的极限位置”这一切线的动态定义埋下伏笔.
导数教学是高中数学教学的重要构成内容,而其中导数的几何意义是刻画函数单调性的重要工具,也是沟通初等数学与高等数学的桥梁.但在实际的教学中,忽视了研究曲线的切线的数学背景,没有对曲线的切线做明确定义,因此很多学生对通过割线来引入切线产生了困惑,以及导致学生容易将其和其他概念相混淆,从而缺乏严谨性.所以,笔者希望通过以下这个教学设计可以更深刻地让学生理解切线的定义.
3 教学设计
通过对切线概念的历史发展过程以及学生认知起点的分析,笔者将从五个环节对“导数的几何意义”进行教学.
3.1 回顾旧知,引入新课
师:在物理课上,我们学过平面镜光的反射,那么要是在凹凸镜上,光是如何反射的呢?
若已知一小球做平拋运动,我们又如何确定它的速度方向呢?
我们很容易确定斜坡的坡度,但拱桥的坡度又如何确定呢?
师:用我们现有知识,以上几个问题能解决嘛?
生:不能.
师:是的,但我们今天所学的内容就可以解决以上问题.进入新课之前,我们先来回顾下初中学过的一个知识.
师:在初中,同学们接触过圆的切线概念 ,那么“圆的切线”有哪几种定义呢?
生1:与圆只有一个公共点的直线称为圆的切线.
生2:与圆心的距离等于半径长的直线称为圆的切线.
生3:过圆半径的外端,且垂直于半径的直线称为圆的切线.
师:对的,那圆的切线定义是否适用于圆锥曲 线呢?
生:不适用.
师:那什么定义能适用于圆锥曲线的切线?
生:与曲线只有一个公共点且不穿过曲线的 直线.
师:同学们刚刚所说的定义就是古希腊数学家给出的适用于圆锥曲线的切线定义,但是适用于更为一般的曲线吗?例如,曲线y=x3的切线.
生:不适用.
师:结合以上问题,今天我们就一起来探索新的切线定义.
3.2 引导探究,获得新知
师:在中国古代有一位著名的数学家刘徽,他用割圆术探求圆心到其多边形一边所在直线的距离.他这样写道:“以六觚之一面乘半径,因而三之,得十二觚之幂.若又割之,次以十二觚之一面乘半径,因而六之,则得二十四觚之幂.割之弥细,所失弥少.割之又割,以至于不可割,则与圆合体,而无所失矣.”
师:下面,我们用几何画板动画模拟割圆术的变化过程.
师:通过这个动画演示,同学们有什么发现呢?
生1:圆内接多边形逐渐与圆合并一起.
生2:圆的切线是圆内接无穷多边形一边所在的直线.
师:很好,那同学们根据自己的观察,能否概括出一般曲线的切线的定义吗?
生:曲线上B点无限逼近A点,割线AB趋近于确定的位置AD,这个确定位置上的直线AD称为点A处的切线,如图1.
师:对的,也就是说,圆的切线是割线的极限位置.且这个结论适用于所有曲线.
3.3 分层解析,巩固理解
师:由切线的定义,接下来我们重点探索切线与导数的关系.
(1)分层解析
题型1:已知过曲线上一点,求切线方程.
过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.
例1 如图2,求曲线C:y=2x3在点(1,2)处的切线方程.
题型2:已知某曲线,求该曲线在某处的导数.
例2 f(x)= 9-x2 ,求f′(2).
(2)思考小结
切线的斜率与导数的符号表达的是同一对象的两个不同侧面,在解决问题过程中要注重它们之间的相互转化.
3.4 思考探究,深化理解
例3 已知f(x)= 1 2? 9-x2 ,求f′(1).思考:函数f(x)= 1 2? 9-x2 的图像是什么曲线?
师:光照射在椭圆上点A处的反射效果与光照射在椭圆在点A处的切线上的反射效果相同,为什么?
师:若将椭圆放大一百倍(图4),我们将会发现什么?
生:椭圆在点A附近的曲线段与椭圆在点A处的切线段重合.
师、生:光照射在曲线段上与切线段上的效果 一致.
师:这就是微积分中重要的以直代曲的数学 思想.
师:在刘徽的割圆术中同样也包含着重要的微积分思想,同学们知道是什么思想吗?
生:以直代曲思想.
师:对的,“割之弥细,所失弥少.割之又割,以至于不可割,则与圆合体,而无所失矣”这段话表达的就是以直代曲思想.
3.5 归纳总结,深化认识
(1)知识:
①切线的定义;
②函数f(x)在x=x 0处的导数f′(x 0)的几何 意义.
(2)思想:体会极限、以直代曲等思想方法.
(3)应用:①“切点—斜率—切线”知一求二;②学生归纳出求切线的一般步骤.
4 叠加模式解析
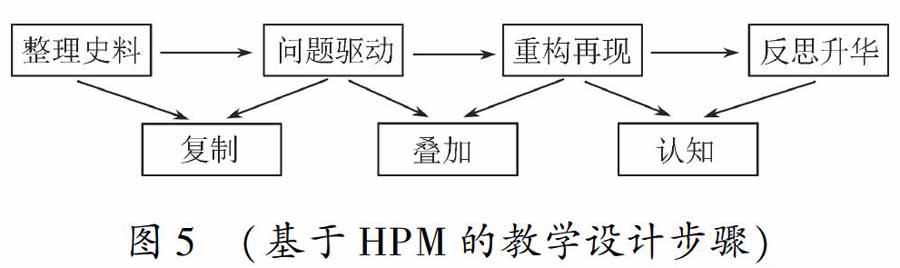
数学史与数学教学的融入是个综合的过程,首先需要对数学史料进行深入的挖掘以及提炼,其次将其融入教材,最后再由教师进行加工运用到教学中.教师运用和加工现有的史料和教材,可以发现一个普遍的教学设计步骤(图5).
下面笔者将基于本文的教学设计就如何挖掘史料,如何将数学史融入教材,从四个环节进行具体的解析,分别是:整理史料→问题驱动→重构再现→反思升华.
整理史料:在对某一个知识的讲解希望加入数学史时,你不能仅仅满足教材上提供的一些历史资料,而需要大量搜索与该知识有关的历史资料.因此,在材料的选取上需要做到以下几点:(1)思考你需要设置什么样的情境,哪些材料具有代表性适合放入情境中;(2)在相关历史材料中,提炼出符合要求的历史材料,从而为情境设置做準备;(3)厘清知识的发展过程,并整理出一条主“脉络”,为重构做准备.
问题驱动:从问题出发,创设情境,从而呈现给学生刺激性数学历史,引起学生学习数学的兴趣,激起学生的好奇心、发现欲,产生认知冲突,诱发质疑猜想,唤醒强烈的问题意识,从而使其发现和提出数学问题,解决数学问题.利用已整理好的史料,根据课程需要达到的效果,直接引用或适当改编史料,设置一个有历史,有故事,有启发的情境为重构做准备.故事情境是为了文化的显性表现,重构则是为了文化的隐性再创造.
重构再现:根据情境中产生的问题,引导学生按照整理史料环节所制定知识的历史“脉络”(引导的方法可多样化,可通过启发、游戏、实践等方式)重构对于这部分知识的发现过程.上述教学设计中,以通过对光的反射问题、速度方向问题以及曲线夹角问题的重构,激发学生的求知欲,再通过教师的巧妙引导,让学生探究求解过程,实现重构.
反思升华:在学生经过亲身体验、深刻领悟后,引导学生回顾该知识的产生过程、发明历史,并让学生自己总结在这一过程中发现了什么,怎么发现的,有什么启发.从而挖掘出其中的数学思想,体味数学的文化,巩固新建构的认识.
5 反思总结
本节课主要通过顺应——重构的叠加模式将数学史融入数学教学.整体上看,先回顾已有圆的切线概念,接着用几何画板演示刘徽的割圆术,以探索新的切线的定义;然后通过两个例子来探索切线与导数的关系,利用几何画板探索以直代曲的数学思想;最后归纳总结整个过程,再现了导数几何意义的历史发展过程,属于重构式.从局部看,重构历史上的数学问题,提炼其背后的数学思想,使历史上的数学问题符合学生现实生活的背景与认知能力,属于顺应式.历史故事作为情境,可以让学生再次回到历史创造环境氛围中去,仿佛身临其境.而后为了解决情境中的问题,教师通过设疑,提示,引导学生重回历史发展之路,探索重构导数的几何意义.数学史中包含着丰富的教学素材和思想养料,包含着不同时代,各个数学家的探索精神和创新思维.如果全然抛弃这些历史素材,数学课堂就变成了一个“模仿作坊”,学生学习到的只是单调的定理,公式,学到的只是一具数学的躯壳,没有灵魂的数学.自然,学生无法体会到历史中数学家的思维之妙,也不能感受多元文化.“重构——顺应”叠加式融入数学史,这一模式,既有“重构”让学生再创造式的探索发现知识,又有“顺应”让学生体会到数学的历史、文化,体会到数学家们精妙的思想,感受数学的魅力.在这样模式下,数学史能更真正有效地服务于教学,HPM也能越走越远.
参考文献
[1] 徐斌艳.2016年相聚在第十三届国际数学教育大会[J].中学数学月刊,2016.
[2] Struik D J. A Source Book in Mathematics, 1200–1800[M]. Inceton: Princeton University Press, 1986.
[3] L Hospital G. Analyse des Infiniment Petits[M]. Aris: De LImprimerie Royale, 1696.
[4] 王芳.数学史融入导数教学的行动研究[D].华东师范大学,2012.


【摘 要】 ?数学史的融入方式直接影响着数学教学的质量.文章以“顺应——重构”叠加模式将数学史融入到数学教学中,以“导数的几何意义”为例设计一则教学案例,再从“整理史料、问题驱动、重构再现、反思升华”四个模块进行分析,从而得到一些启示,以期为数学史融入数学教学起到些许借鉴作用.
【关键词】 ?叠加模式;数学史;数学教学;导数的几何意义;教学设计
以HPM视角融入到教材设计和课堂教学,日益受到一线教育工作者的关注.2016年在德国汉堡大学举行的第十三届国际数学教育大会中第25个研究专题强调,要认识数学史在数学课堂和教学中的作用 [1].
根据汪晓勤教授的划分,数学史融入到数学教学的模式可分为以下四种:分别是附加式、复制式、顺应式和重构式.其中重构式指借鉴或重构知识发生、发展的历史,浓缩概念发展的过程,让学生经历概念的形成过程,其教学目的主要为加深对概念的纵向与横向的理解.其更注重的是将数学史知识融入在认知方面的作用.而顺应式主要指改编历史上的数学问题、方法,提炼其背后的数学思想,其教学目的主要是在教学过程中渗透重要的数学思想.两者虽各有所长,但彼此也都存在一些缺陷.比如,重构式难度较大,缺少直观性,易使课堂枯燥;而顺应式较浅显,不易挖掘出知识的内涵.现今,我国中学数学教材对于数学史的融入大都以单独的方式,如若将它们结合起来,在“顺应式”中融入“重构式”,显然会使教学更优化.因此,笔者将以“导数的几何意义”教学设计及分析为例来探讨“顺应——重构”叠加模式的运用.
1 切线概念的发展历史
通过数学史的简单介绍,笔者了解到切线概念的形成过程,是经历了由静态到动态的一个发展过程.古希腊数学家欧几里得最早定义了圆的切线,接着阿波罗与阿基米德用欧几里得的方法定义了圆锥曲线与螺线曲线,而那时在古代数学中,切线的定义还局限于静态的定义——与曲线只有一个公共点且位于曲线一侧(或“不穿过”曲线)的直线.
直到17世纪,数学家相继发现和研究了一般曲线的不同构造法.其中,巴罗利用“特征三角形”的概念——实质上把切线看作是割线的极限位置.而直到17世纪下叶,切线为割线之极限位置的思想才成为数学家的共识.德国数学家莱布尼茨将曲线的切线定义为“连接曲线上无限接近两点的直线”,或“曲线的内接无穷多边形的一条连续边” [2].法国数学家洛必达在其《无穷小分析》中亦将曲线的切线定义为曲线的内接“无穷多边形”一边的延长线 [3].
可见,切线定义从静态走向动态跨越了数千年的岁月,而了解切线的发展历史,有利于教师把握学生的认知起点,也为教学设计打开了新的视野.
2 学生的认知起点
学生对切线的认知起点是圆的切线,因而教师首先可以从圆出发,让学生回顾圆的切线的定义.圆的切线主要有3种定义方式,分别为:与圆只有一个公共点的直线;过圆上一点且垂直于该点与圆心连线的直线;到圆心的距离等于圆的半径的直线.其次,让学生反思,上述定义是否适用于圆锥曲线呢?显然不适用,以抛物线为例,对称轴与抛物线只有一个交点,但不是切线.学生很自然会对定义添加约束条件,得到“与曲线只有一个公共点且不穿过曲线的直线”.这就是古希腊数学家给出的适用于圆锥曲线的切线定义,但是适用于更为一般的曲线吗?反之,直线与三角函数y=sinx的图象有不止一个交点,它是曲线的切线吗?所以,切线概念的教学必须让学生认识到“是否只有一个公共点”也不是切线的判别标准,激发学生寻求新的切线定义,为形成“切线是割线的极限位置”这一切线的动态定义埋下伏笔.
导数教学是高中数学教学的重要构成内容,而其中导数的几何意义是刻画函数单调性的重要工具,也是沟通初等数学与高等数学的桥梁.但在实际的教学中,忽视了研究曲线的切线的数学背景,没有对曲线的切线做明确定义,因此很多学生对通过割线来引入切线产生了困惑,以及导致学生容易将其和其他概念相混淆,从而缺乏严谨性.所以,笔者希望通过以下这个教学设计可以更深刻地让学生理解切线的定义.
3 教学设计
通过对切线概念的历史发展过程以及学生认知起点的分析,笔者将从五个环节对“导数的几何意义”进行教学.
3.1 回顾旧知,引入新课
师:在物理课上,我们学过平面镜光的反射,那么要是在凹凸镜上,光是如何反射的呢?
若已知一小球做平拋运动,我们又如何确定它的速度方向呢?
我们很容易确定斜坡的坡度,但拱桥的坡度又如何确定呢?
师:用我们现有知识,以上几个问题能解决嘛?
生:不能.
师:是的,但我们今天所学的内容就可以解决以上问题.进入新课之前,我们先来回顾下初中学过的一个知识.
师:在初中,同学们接触过圆的切线概念 ,那么“圆的切线”有哪几种定义呢?
生1:与圆只有一个公共点的直线称为圆的切线.
生2:与圆心的距离等于半径长的直线称为圆的切线.
生3:过圆半径的外端,且垂直于半径的直线称为圆的切线.
师:对的,那圆的切线定义是否适用于圆锥曲 线呢?
生:不适用.
师:那什么定义能适用于圆锥曲线的切线?
生:与曲线只有一个公共点且不穿过曲线的 直线.
师:同学们刚刚所说的定义就是古希腊数学家给出的适用于圆锥曲线的切线定义,但是适用于更为一般的曲线吗?例如,曲线y=x3的切线.
生:不适用.
师:结合以上问题,今天我们就一起来探索新的切线定义.
3.2 引导探究,获得新知
师:在中国古代有一位著名的数学家刘徽,他用割圆术探求圆心到其多边形一边所在直线的距离.他这样写道:“以六觚之一面乘半径,因而三之,得十二觚之幂.若又割之,次以十二觚之一面乘半径,因而六之,则得二十四觚之幂.割之弥细,所失弥少.割之又割,以至于不可割,则与圆合体,而无所失矣.”
师:下面,我们用几何画板动画模拟割圆术的变化过程.
师:通过这个动画演示,同学们有什么发现呢?
生1:圆内接多边形逐渐与圆合并一起.
生2:圆的切线是圆内接无穷多边形一边所在的直线.
师:很好,那同学们根据自己的观察,能否概括出一般曲线的切线的定义吗?
生:曲线上B点无限逼近A点,割线AB趋近于确定的位置AD,这个确定位置上的直线AD称为点A处的切线,如图1.
师:对的,也就是说,圆的切线是割线的极限位置.且这个结论适用于所有曲线.
3.3 分层解析,巩固理解
师:由切线的定义,接下来我们重点探索切线与导数的关系.
(1)分层解析
题型1:已知过曲线上一点,求切线方程.
过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.
例1 如图2,求曲线C:y=2x3在点(1,2)处的切线方程.
题型2:已知某曲线,求该曲线在某处的导数.
例2 f(x)= 9-x2 ,求f′(2).
(2)思考小结
切线的斜率与导数的符号表达的是同一对象的两个不同侧面,在解决问题过程中要注重它们之间的相互转化.
3.4 思考探究,深化理解
例3 已知f(x)= 1 2? 9-x2 ,求f′(1).思考:函数f(x)= 1 2? 9-x2 的图像是什么曲线?
师:光照射在椭圆上点A处的反射效果与光照射在椭圆在点A处的切线上的反射效果相同,为什么?
师:若将椭圆放大一百倍(图4),我们将会发现什么?
生:椭圆在点A附近的曲线段与椭圆在点A处的切线段重合.
师、生:光照射在曲线段上与切线段上的效果 一致.
师:这就是微积分中重要的以直代曲的数学 思想.
师:在刘徽的割圆术中同样也包含着重要的微积分思想,同学们知道是什么思想吗?
生:以直代曲思想.
师:对的,“割之弥细,所失弥少.割之又割,以至于不可割,则与圆合体,而无所失矣”这段话表达的就是以直代曲思想.
3.5 归纳总结,深化认识
(1)知识:
①切线的定义;
②函数f(x)在x=x 0处的导数f′(x 0)的几何 意义.
(2)思想:体会极限、以直代曲等思想方法.
(3)应用:①“切点—斜率—切线”知一求二;②学生归纳出求切线的一般步骤.
4 叠加模式解析
数学史与数学教学的融入是个综合的过程,首先需要对数学史料进行深入的挖掘以及提炼,其次将其融入教材,最后再由教师进行加工运用到教学中.教师运用和加工现有的史料和教材,可以发现一个普遍的教学设计步骤(图5).
下面笔者将基于本文的教学设计就如何挖掘史料,如何将数学史融入教材,从四个环节进行具体的解析,分别是:整理史料→问题驱动→重构再现→反思升华.
整理史料:在对某一个知识的讲解希望加入数学史时,你不能仅仅满足教材上提供的一些历史资料,而需要大量搜索与该知识有关的历史资料.因此,在材料的选取上需要做到以下几点:(1)思考你需要设置什么样的情境,哪些材料具有代表性适合放入情境中;(2)在相关历史材料中,提炼出符合要求的历史材料,从而为情境设置做準备;(3)厘清知识的发展过程,并整理出一条主“脉络”,为重构做准备.
问题驱动:从问题出发,创设情境,从而呈现给学生刺激性数学历史,引起学生学习数学的兴趣,激起学生的好奇心、发现欲,产生认知冲突,诱发质疑猜想,唤醒强烈的问题意识,从而使其发现和提出数学问题,解决数学问题.利用已整理好的史料,根据课程需要达到的效果,直接引用或适当改编史料,设置一个有历史,有故事,有启发的情境为重构做准备.故事情境是为了文化的显性表现,重构则是为了文化的隐性再创造.
重构再现:根据情境中产生的问题,引导学生按照整理史料环节所制定知识的历史“脉络”(引导的方法可多样化,可通过启发、游戏、实践等方式)重构对于这部分知识的发现过程.上述教学设计中,以通过对光的反射问题、速度方向问题以及曲线夹角问题的重构,激发学生的求知欲,再通过教师的巧妙引导,让学生探究求解过程,实现重构.
反思升华:在学生经过亲身体验、深刻领悟后,引导学生回顾该知识的产生过程、发明历史,并让学生自己总结在这一过程中发现了什么,怎么发现的,有什么启发.从而挖掘出其中的数学思想,体味数学的文化,巩固新建构的认识.
5 反思总结
本节课主要通过顺应——重构的叠加模式将数学史融入数学教学.整体上看,先回顾已有圆的切线概念,接着用几何画板演示刘徽的割圆术,以探索新的切线的定义;然后通过两个例子来探索切线与导数的关系,利用几何画板探索以直代曲的数学思想;最后归纳总结整个过程,再现了导数几何意义的历史发展过程,属于重构式.从局部看,重构历史上的数学问题,提炼其背后的数学思想,使历史上的数学问题符合学生现实生活的背景与认知能力,属于顺应式.历史故事作为情境,可以让学生再次回到历史创造环境氛围中去,仿佛身临其境.而后为了解决情境中的问题,教师通过设疑,提示,引导学生重回历史发展之路,探索重构导数的几何意义.数学史中包含着丰富的教学素材和思想养料,包含着不同时代,各个数学家的探索精神和创新思维.如果全然抛弃这些历史素材,数学课堂就变成了一个“模仿作坊”,学生学习到的只是单调的定理,公式,学到的只是一具数学的躯壳,没有灵魂的数学.自然,学生无法体会到历史中数学家的思维之妙,也不能感受多元文化.“重构——顺应”叠加式融入数学史,这一模式,既有“重构”让学生再创造式的探索发现知识,又有“顺应”让学生体会到数学的历史、文化,体会到数学家们精妙的思想,感受数学的魅力.在这样模式下,数学史能更真正有效地服务于教学,HPM也能越走越远.
参考文献
[1] 徐斌艳.2016年相聚在第十三届国际数学教育大会[J].中学数学月刊,2016.
[2] Struik D J. A Source Book in Mathematics, 1200–1800[M]. Inceton: Princeton University Press, 1986.
[3] L Hospital G. Analyse des Infiniment Petits[M]. Aris: De LImprimerie Royale, 1696.
[4] 王芳.数学史融入导数教学的行动研究[D].华东师范大学,2012.

