以数轴之引，渗透“用字母表示数”

    丁增宝 刘斌 高圣前 胡平

    

    

    

    [摘要]从引入的真正目的为出发点，思考引入在一节课所处的位置和扮演的角色，悟出“引入观”，据此想法设计教学案例《用字母表示数》，以数轴为媒介，让引入的作用发挥到极致，对学生学习新知、后续学习将产生积极的促进作用，并通过两次教学实践。再次印证“引入观”是值得深思的。

    [关键词]引入，数轴，用字母表示数，初高中联系

    1 笔者的“引入观”

    优秀文学作品的开头是全文的精髓，是引线，表达着作者的态度和思想，全文延续着开头的态势持续发展，如《三国演义》《红楼梦》均是如此，故笔者之思考，教学中的引入应如文学作品的开头一般，上引听者之心，下引内容之魂，教师在教学时。应该让引入具有“灵魂性”，笔者所指“灵魂性”，蕴含三个观点：一是引入应该体现教学内容的前后联系，起到承上启下的作用：二是引入应该为理解新知提供一种新的视角和解决问题的路径，有效促进顺向迁移的作用：三是引入与新课相互融合应该为后续学习做好充分的准备，起到铺垫作用，本文以沪科版第二章第一节“用字母表示数”为案例，具体阐述笔者的“引入观”。

    2 教学设计

    本节“用字母表示数”是初中生从数到代数的第一课，是具体到抽象的飞跃，是知识螺旋式上升的体现，因为在小学已经初步了解“用字母表示数”，并会字母进行简单的列式，因此人教版、沪科版和北京教育出版社的教材在引入环节均采用小学的列式，然后逐步理解用字母表示数，利用与小学知识的相互联系，的确是一种很好的引入方式。但是从时间和空间上看，这种引入显得有些遥远和刻意，能否用“就近”的知识引入本节课呢？笔者认为“数轴”就是一个妥当的选择，首先，从宏观（学习内容编排）上看，用字母表示数是在有理数学习之后。因为这遵循学生的认知发展规律：从具体到抽象，从微观上看，有理数可以用数轴上的点表示，事实上，数轴上的点不仅可以表示数，也可以表示一个代数式，这是数与代数式（非数）的共性，何不利用这种共性呢？这也是笔者提到的“承上启下”，其次，从学生的角度思考，数轴是学生今后解决问题的常用工具，甚至到高中仍有着一席之地，后文有说明，因为数轴体现了数形结合思想，使得抽象的数或代数式用一种直观的图象展示，更有助学生理解难点，鉴于此。笔者设计本节的引入，限于篇幅，本文只展示部分教学内容。

    （1）以数轴之引，引入新知

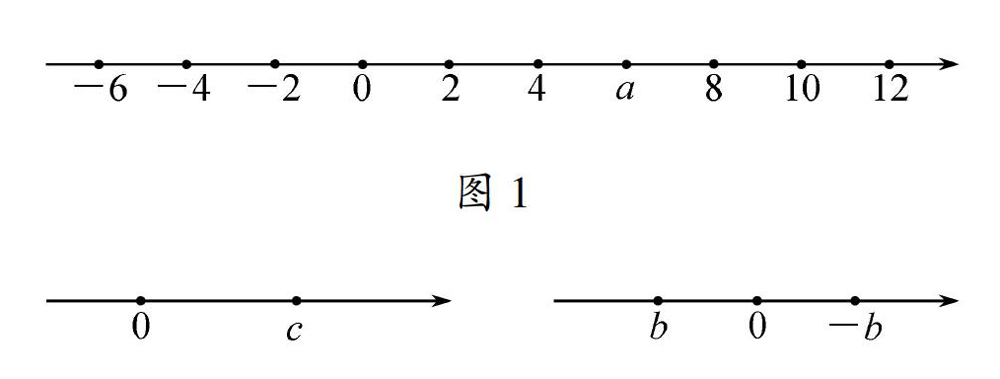
    有理数可以用数轴上的点表示，这是学生在学习数轴时已经掌握的基本事实，数轴的出现，让空洞的有理数变得可形象，可操作。可直观，其实，在学习数轴时，学生已经接触了用字母表示数，如图1、图2、图3均是用字母表示数的雏形，这些题目已经在渗透用字母表示数的思想，因此在本节知识的引人时，我们何必苦苦思索呢？利用数轴的即可完成引入，

    教师：前面一章已经学习了有理数，并且知道有理数可以用数轴上的点表示，请看图1、图2、图3.你们知道这些字母都代表什么意思吗？

    学生1：a表示数6.C表示任意的正数，b与-b表示互为相反数，

    教师：由此可见，这里的字母都表示什么？

    学生（共同）：都表示数，

    教师：这也就是今天所要学习的“用字母表示数”。

    设计意图 新课的引入是一节课的伊始，从时间分配上大概是3分钟，但是新课的引入是为了什么？引入的真正的作用是什么？以笔者之陋见，引人是能启发学生想象力、发散学生思维，激发学生学习的兴趣，激发学生探索新知的好奇心，这是“为什么要引人”，引入是将学生已经学习的旧知与新知充分联系起来，起到承上启下的作用，更是为新课打开一种视野，为探究新知提供一种方法，助于学生理解掌握新知，并在今后的解决问题时起到积极的促进作用，这是“引入真正的目的”，这是笔者提倡“引入观”的第一个观点：引入应该体现教学内容的前后联系，起到承上启下的作用，

    （2）以数轴之引，探究偶数

    因为数轴和图l、图2、图3的引入，使得数到字母的“无缝过渡”，从而，学生对抽象的概念“字母表示数”显得可触及，可操作，接下来。继续利用数轴探究新知：偶数，

    教师：请同学们看图1.我们把数轴无限拉伸，在非负半轴上显现出来的数分别为0.2.4.6.8.……，这些数在小学中我们称之为什么数？（教师把这些数用黑点标注出来）。

    学生2：都是偶数，

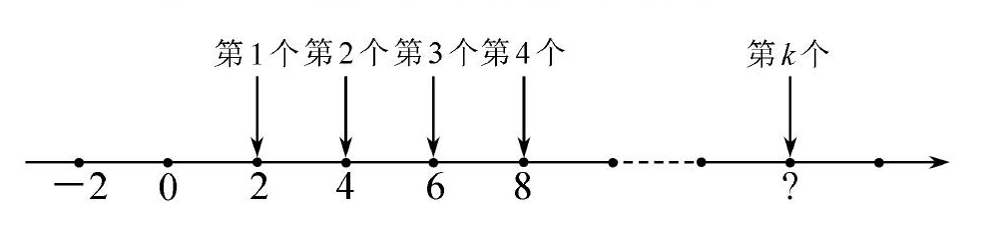
    教师：因为负数的学习，所以偶数不局限于正数，偶数的定义为：能够被2整除的数，故偶数分别为0.±2.±4.±6.…请同学们继续观察图4.你知道问号处表示多少吗？请说说你的想法，

    学生3：是2k，因为每一个对应的数均是第几个的2倍。所以为2k，

    教师：此时k是什么数？

    学生3：k是正整数，

    教师：那2k是偶数吗？

    学生4：是的，因为它满足偶数的定义：从数轴上看，它正好在偶数点上，

    教师：现在我们把上面的提示抹掉，只剩下单纯的数，当k是非正整数时，2k对应的是哪些数？你可以在数轴上表示出来吗？

    学生5：分别是0.-2.-4.-6等等，

    教师：请大家观察我们刚刚标出这些点，它们是什么数？

    学生6：都是偶数，

    教师：请思考，任何一个偶数，可以用什么形式表示出来呢？需要注意什么？

    学生7：2k，其中k为整数，

    教师：请大家继续观察这个数轴图5.能否说出点A、点B分别表示什么？

    学生8：A表示2K-2.O表示2K+2.

    教师：若k是任意的整数，那么2k-2和2k+2都可以表示任何一个偶数吗？请同學们小组讨论，

    经过小组的讨论和辩论，得出一致的结论：若k是任意的整数，那么2k-2和2k+2都可以表示任何一个偶数。

    教师：既然2k，2k-2和2k+2都可以表示任意的偶数，从形式的简洁性看，哪个形式更受欢迎？

    学生（共同）：2k，

    设计意图在小学，学生对偶数的概念仅仅停留在正偶数，学习有理数之后，偶数的范围扩大到整数范围内，那么借助于数轴认识偶数更直观，使得虚无缥缈的的负偶数变得可观察，学生理解偶数之后。可以继续利用数轴自主探究奇数，并且从数轴上观察奇数与偶数的排列，更能凸显奇偶数的规律和内涵，本环节，仅仅用一条数轴，就能引导学生认识偶数的一般形式，和初步理解字母表示数，这条数轴在后面将继续发挥作用。

    （3）以数轴之引，拓展新知

    学生在数轴的引导下。继续探究新知并由此应用新知，教师展示下面的例题。

    例1：观察图6中正方形四个顶点所标的数字规律，可知，数2016应标在（）。

    A，第504个正方形的左上角

    B，第504个正方形的右上角

    C，第505个正方形的左上角

    D，第505个正方形的右下角

    教师：根据观察，你有哪些发现？

    学生9：每个正方形右下角的数分别为0.4.8.12.…都是4的倍数，2016也能被4整除，

    教师：你能否把这些数标在数轴上？第n个如何表示？

    学生展示图7.

    教师：通过以上的分析。你能得出本题的选项？

    学生（共同）：选D。

    设计意图 若是把数标在数轴上，本题就转化为数轴上的数，从形式上化简，从难度上降低，如此观察，让规律更加显现，让字母表示数的内涵更加深入，表示4的倍数可以表示诸如4n，4n+4.4n-4（n为整数）的形式，这既是对偶数概念的巩固，也是对知识的应用和深化，在此特别说明。例1学生的生成的知识很多，与本文相关的只展示学生9的回答。

    将例题的数标在数轴上，也就是现在所学与已经学习的数轴建立相互联系，拓展了解题的思路，使得问题简单化，为本题提供一种解决问题的方法，这即是前文提到的第二观点：引人为理解新知提供一种新的视角和解决问题的路径，有效促进顺向迁移的作用，这样的教学让学生从心里上产生简单易学，对新知产生亲近感、无陌生感，在学习中，学生会发现，字母不仅可以表示数，亦可表示代数式，如一6.2k，4n-4等等，中考常常考察的探索规律的题目，让学生通过规律总结归纳出数列的通项公式，这何尝不是一种用字母表示数呢？形如an=4n-4（n为正整数），高中学生会明白这是一个以O为首项，以4为公差的等差数列，4n-4可以看成是等差数列的通项公式，只不过，在初中生的眼中，4n-4是4的整数倍，这既是与字母表示数的相互联系，也是初高中的相互联系，从理论上讲，等差数列的每一项都是数轴上一些等距离排列的点，从这个角度，数轴是连接数与代数式的纽带，借助数轴可以深化理解用字母表示数，

    3 为什么选择数轴作为引入

    其一，“用字母表示数”引入的方式有很多，如寻物启事、由小学所学知识、有理数的运算律等等，这都是常见的引入，这种引入都是从学生身边作为出发点，学生也非常认可这种引入，但是笔者看来，该引入的目的過于“单纯”，因为这种引入，在后面的新知探究所用甚少，此种引入仅仅是“因为新知的引用而引用”，引入的真正的作用是贯穿始终，如卫德彬在文中《数学开放型问题及其教学实践与思考》提供一种想法，引人的例题是开放型的问题，使得探究的问题有路径可循，在一定程度上，这种想法体现了积累数学活动经验的思想，使得后续的学习更为流畅和顺利，本文亦赞同这种思想，让引入的作用更宽广，更具有“延续性”，其二，数轴是学生前面已经学习的旧知，当教师把数和表示数的字母标在数轴上，使得本节知识丰富饱满、立体可见，从学生的理解角度上看，学生更乐于接受这种可见、可触摸的引入，让难点转化，其三，大部分的学生会接受

    4 实际情况与实践反馈

    笔者秉承本文中的思想，于2019年9月19日在合肥市第五十中学东校区（非笔者学校）把本节课完整地呈现给学生，由于开学只有短短的20天，事实上，学生并没有完整地学习完第一章节的内容，只学习了1.1正数和负数、1.2数轴、相反数和绝对值、1.3有理数的大小、1.4有理数的加减，学生在此期间，接触最多就是数轴，如借助数轴学习相反数、绝对值、及有理数的加减，所以，数轴在分析问题方面，起着重要的作用，从前文的阐述中，数轴除了帮助学生学习新知，在后面的继续学习中继续扮演中重要的角色，对学习起着积极的作用，因此萌发借助数轴认识“用字母表示数”，在学习有理数的大小时，学生已经接触过如“-b，a+b”等等在数轴上表示，这就是代数思想的萌芽，也是笔者选择数轴的初衷，评课教师用“耳目一新”来形容，评价本节课用一种全新的视角学习本节课，令抽象的、陌生的代数变得直观形象，现场的学生反馈就是更好的证明，笔者曾经疑虑：是否合肥市第五十中学的学生太“懂事”了，有意配合授课教师作出如此好的教学效果？于是，2019年9月23日，笔者整理本次课件，结合学生的情况。只对其中的练习题目作出适当的修改，并请本校教师一同听课，结果教学效果如19日当天一样，并收到听课教师的一致好评，两次实践，更令笔者坚信：实践出真知，以数轴之引，渗透“用字母表示数”是值得一试的教学尝试，也间接对笔者的引入观又一次肯定。