基于ADINA的桩土相互作用分析
崔春义 孟坤 程学磊 杨刚

摘要:基于大型通用数值计算平台ADINA建立三维数值模型,分别结合相互作用三维接触模型和p-y曲线简化分析模型模拟桩土系统在水平荷载作用下的桩顶位移变化规律,计算分析表明:计算结果与实际测量值基本一致,验证了两种建模方式的合理性和正确性。在此基础上进一步对p-y,曲线简化分析模型在不同水平荷载作用下的工作性状进行分析,计算结果表明p-y,曲线简化分析模型能较好地模拟桩土间的相互作用行为,将其应用到桩基相关抗震设计中能明显减少计算求解消耗。
关键词:ADINA;桩土相互作用;p-y曲线;三维数值分析
中图分类号:TU391;TU293.5 文献标识码:A 文章编号:1000-0666(2016)01-0096-05
0 引言
桩土相互作用在桥梁抗震分析中占有非常重要的地位,地震作用通过土运动将横向荷载传给桩基,分析水平荷载作用下桩土相互作用对桥梁抗震设计具有一定的指导意义。
桩基水平承载力的计算方法主要有3种,分别是有限元方法、弹性分析法和地基反力法。地基反力法即温克尔地基梁模型法(燕斌,2007),该法将桩视为埋置于土介质中的梁,桩周土体用相互独立的弹簧和阻尼器来表示,在考虑土抗力沿深度的变化同时还可以考虑土的非线性性质,但忽略了土的连续性。这一方法物理概念清晰,计算工作量少,在地基的设计和分析中被广泛地应用。
地基反力法中p-y曲线法是在水平力作用下,地面下深度z处的土抗力P与该点的挠度y之间的关系曲线,综合反映了桩周土的非线性,桩的刚度和外荷载作用性质等特点(肖晓春等,2002)。
以往的研究工作中由于当时计算理论和硬件条件限制,诸多桩土相互作用分析都对地基模型进行线性简化处理,或利用二维模型进行简化分析。本文将采用大型通用数值分析平台ADINA,对横向荷载作用下的桩土相互作用进行三维数值模拟,分析其在水平荷载作用下桩顶的最大位移。然后根据API规范规定的P-y曲线,用非线性弹簧模拟桩土的相互作用,建立桩土相互作用的简化分析模型,将其在水平荷载作用下的桩顶位移与三维数值模型以及实际测定值之间进行比较,说明API规范规定的p-y曲线的适用性。将p-y曲线简化分析方法应用到大型桥梁的抗震分析中,在保证计算精度的前提下能大大减少计算量,具有非常重要的工程实际意义。
1 数值分析模型
本文采用ADINA中的摩尔一库伦材料模拟土体。库伦摩擦定律是土力学中的一个基本定律,按照这个定律,破坏面上剪切应力τf与法向应力σf之间满足下列关系式:
τf=c+σftanφ. (1)式中,c为黏聚力,φ为内摩擦角。
用摩尔应力圆表示,上述条件相当于破坏应力圆将与一条称为强度包线的直线相切。用主应力表示,式(1)可改写为将上述摩尔-库伦强度理论推广于塑性应变理论,即假定屈服条件也不受中主应力的影响。具有这种性质的材料称为摩尔-库伦材料(刘成宇,华祖馄,2009)。
三维桩土数值模型的参数设置如下:桩周土范围取桩半径的20倍,很多理论分析和计算结果证明了当桩周土范围足够大时其边界对桩身位移的影响非常小,因此取边界条件为:模型底部以及桩周土均采用全约束(袁志林等,2011)。
考虑到模型的对称性,只建立一半的真实模型,所有对称面在外法线上的位移是约束的,但在对称面上可以自由移动,采用对称约束,模型顶面上所有节点在各个方向上都是自由的。
本文使用试桩资料来自江苏镇江大港(1982)地区的试验(陈洪,2004),试桩基本资料如表1所示,地质资料如图1所示。
在模型中,桩体和土体采用8节点实体单元,用各项同性模型进行模拟。土体的变形包括弹性应变和塑性应变,是一种典型的弹塑性介质。土体的材料特性复杂、种类繁多,根据已知土体的不同参数,所对应的本构模型也有所不同,计算结果存在差异。因此模拟桩土间的相互作用时恰当地选取土体的本构模型,对于整个数值分析过程非常重要(李海林,2006)。目前应用比较多的是摩尔一库伦材料,在ADINA中用摩尔一库伦材料模拟土体,各个土层的属性根据图1中的各层地质资料进行输入。
在ADINA中通过建立接触对模拟桩土间的相互作用,首先在桩土界面上建立接触面,然后建立相互对应的接触对。接触对中接触面的选择需要满足一定的原则,即选择刚度大、自由度相对较少的面即桩表面为Target Surface,土体刚度较小自由度相对较多为Contaetor Surface。桩土之间的库伦摩擦系数取为0.2(周月慧等,2007)。建立的三维有限元模型如图2所示。
2 p-y曲线简化分析模型
根据API规范中规定的软粘土的p-y曲线公式,计算出单位桩长的极限土抗力为式中,y为由地面到深度z处的土的平均有效重度;cu为土的不排水抗剪强度;z为土的深度;d为桩的边宽或直径;J为实验系数,一般J=1/2,较硬的土取J=0.25。
土阻力达到极限土阻力一半时的相应变位为式中,y50为被动侧土达到极限水平抗力的一半时相应深度处桩的侧向变形(胡胜刚,2005);ε50为约一半的最大主应力差时的土的应变值,按表2取值。
桩径d计算值(徐鹏举等,2010)按下面方法求得:(1)圆形截面桩:实际桩径D>1m时,取d=0.9(1+D);实际桩径D≤1m时,取d=0.9(0.5+1.5D)。(2)方形截面桩:实际桩宽B>1m时,计算桩宽取d=B+1;实际桩宽B≤1m时,取d=1.5B+0.5。
由此确定p-y曲线为当y=8y50时,土达到p/pu=1的极限,此后保持为定值。软粘土的p-y曲线如图3所示。
根据计算出的p-y曲线,转化出力与位移之间关系的具体数值,输入ADINA中,生成非线性弹簧,模拟桩土之间的相互作用。
桩体采用二维梁单元模拟,桩底为固定约束,桩土之间的相互作用通过p-y曲线生成的非线性弹簧来模拟。模型总共设置了15个弹簧单元,在桩上节点与大地之间设置弹簧,计算模型如图4所示:
3 计算结果分析
3.1 P-y曲线对比分析
按照试桩试验的加载方式,在有限元计算中,同样施加49.0kN、98.0kN、147.1kN、196.1kN和245.2kN的横向水平荷载,计算得出桩顶水平位移。
由计算结果可知,三维数值分析模型计算的桩顶水平位移更接近实测位移,计算结果较p-y曲线简化分析模型计算得出的桩顶水平位移小。三维模型计算结果差异性产生的原因主要有:三维分析模型土体本构关系的选取与实际土体存在一定的差异,接触面相关参数的选取同样会影响计算结果。
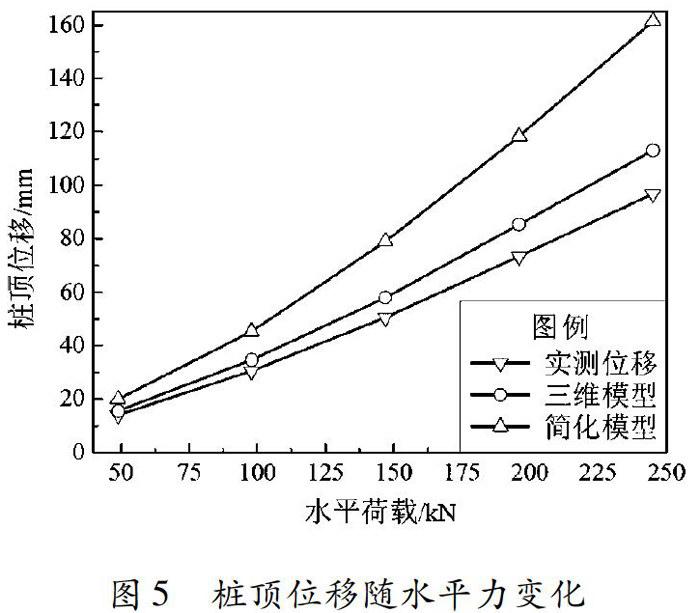
镇江大港试桩在各级荷载作用下桩顶水平位移的实测值与三维数值模型和P-y曲线简化分析模型计算结果的比较如表3所示。镇江大港桩顶位移随水平力变化如图5所示。
随荷载的增大p-y曲线模型的计算结果误差也越来越大,造成这一结果的原因主要有:非线性弹簧模拟桩土间相互作用本身的近似性因素(李炜等,2011),同时所采用的P-y曲线是根据美国Austin地区的试验资料构造,应用到其他地区会存在一定的误差(曹维科,2011)。因此想要更好地应用p-y曲线简化模型模拟桩土之间相互作用,必须根据试桩所在地的地质资料,寻找适合本地区的p-y曲线。
3.2 桩身变形分析
桩受到横向荷载作用时,桩身的变形主要为水平向的挠曲。在不同水平向荷载作用下桩土相互作用的P-y曲线简化分析模型中桩身的水平位移沿埋深的变化如图6所示。由图6可知,随着荷载的逐渐增大桩身位移越来越大,荷载增大到一定程度之后,桩顶的位移增大幅度呈增长趋势。桩身位移沿埋深的变化充分说明了桩土之间相互作用的非线性,当荷载增到一定程度之后,桩逐渐达到极限状态,趋于破坏,桩顶位移急剧增大。
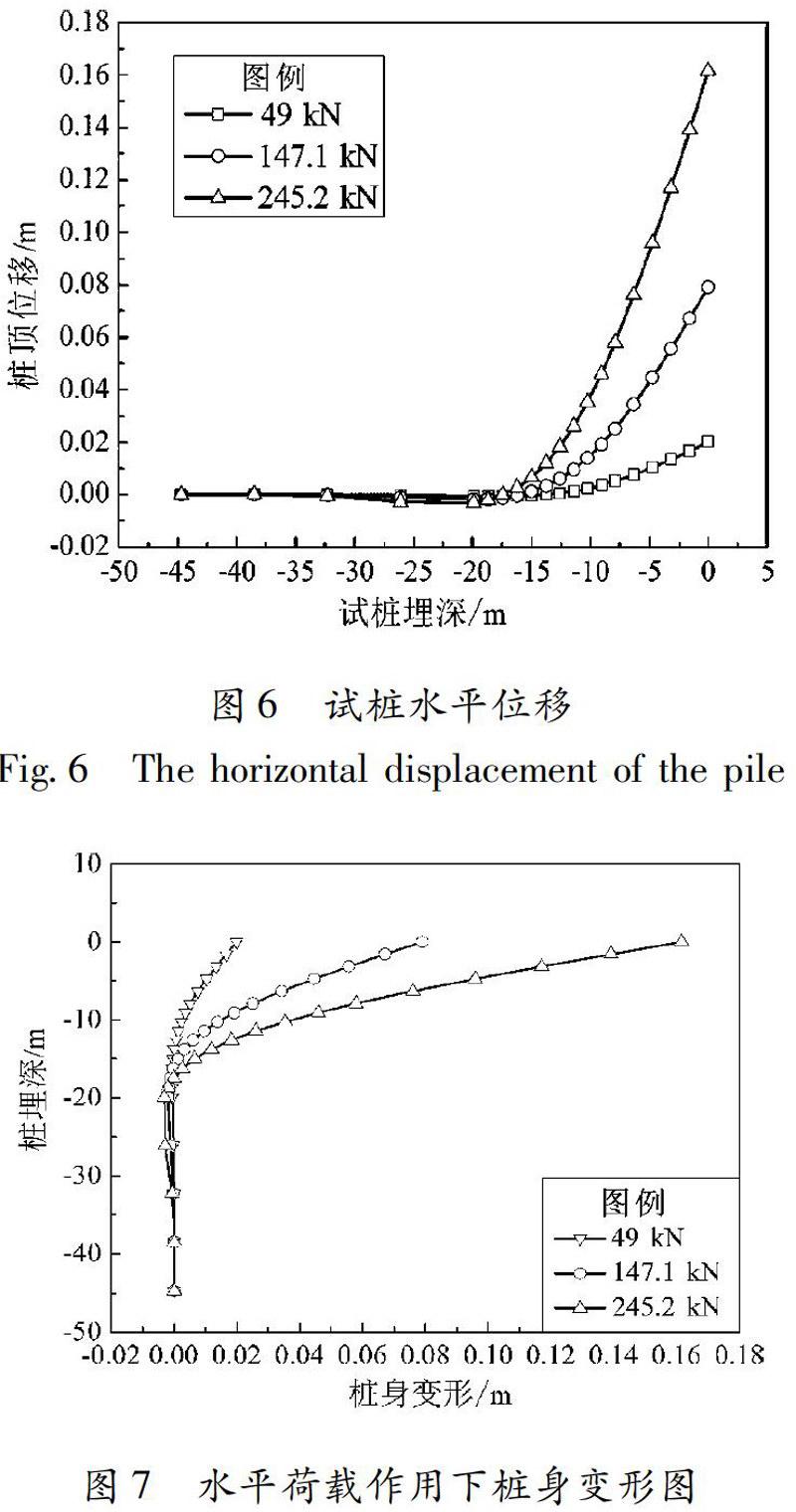
桩在49.0kN、147.1kN、245.2kN水平荷载作用下的桩身变形如图7所示,可以看出,桩顶位移随荷载的增大而增大,埋深达到15m后,桩身位移随荷载增大变化并不明显。桩身位移在桩顶处达到最大值,然后沿桩深逐渐减小,到桩体位移为零后,桩体位移开始反向增大,增大到一定值后又开始减小,到桩底时位移为零,很符合柔性长桩的特性(刘延芳,2014)。
4 结论
采用大型通用数值分析平台ADINA对水平荷载作用下桩基的工作性状进行分析,分别建立了横向荷载作用下的桩土相互作用三维有限元数值分析模型与p-y曲线简化分析模型。计算分析表明:
(1)三维有限元数值分析模型所得的计算结果与实际测量的结果基本一致,而应用API规范中规定的p-y曲线计算的桩顶位移与实测值之间相差较大,说明API规范中规定的p-y曲线有一定的局限性,只适用于与Austin地区地质情况大致相同的地区。
(2)p-y曲线模拟桩土间相互作用简化分析模型在不同水平荷载作用下的工作性状进行分析,计算结果与桩基实际受力性能基本一致,说明p-y曲线能较好地模拟桩土间的相互作用。这样,应用P-y曲线法须先根据本地区的地质资料由实验或者三维分析的方法求得适合本地区的p-y曲线。
(3)在保证计算精度的前提下,将P-y曲线模拟桩土间相互作用的简化计算方法应用到桩基抗震设计中能大大减少计算消耗,具有非常重要的工程现实意义。



摘要:基于大型通用数值计算平台ADINA建立三维数值模型,分别结合相互作用三维接触模型和p-y曲线简化分析模型模拟桩土系统在水平荷载作用下的桩顶位移变化规律,计算分析表明:计算结果与实际测量值基本一致,验证了两种建模方式的合理性和正确性。在此基础上进一步对p-y,曲线简化分析模型在不同水平荷载作用下的工作性状进行分析,计算结果表明p-y,曲线简化分析模型能较好地模拟桩土间的相互作用行为,将其应用到桩基相关抗震设计中能明显减少计算求解消耗。
关键词:ADINA;桩土相互作用;p-y曲线;三维数值分析
中图分类号:TU391;TU293.5 文献标识码:A 文章编号:1000-0666(2016)01-0096-05
0 引言
桩土相互作用在桥梁抗震分析中占有非常重要的地位,地震作用通过土运动将横向荷载传给桩基,分析水平荷载作用下桩土相互作用对桥梁抗震设计具有一定的指导意义。
桩基水平承载力的计算方法主要有3种,分别是有限元方法、弹性分析法和地基反力法。地基反力法即温克尔地基梁模型法(燕斌,2007),该法将桩视为埋置于土介质中的梁,桩周土体用相互独立的弹簧和阻尼器来表示,在考虑土抗力沿深度的变化同时还可以考虑土的非线性性质,但忽略了土的连续性。这一方法物理概念清晰,计算工作量少,在地基的设计和分析中被广泛地应用。
地基反力法中p-y曲线法是在水平力作用下,地面下深度z处的土抗力P与该点的挠度y之间的关系曲线,综合反映了桩周土的非线性,桩的刚度和外荷载作用性质等特点(肖晓春等,2002)。
以往的研究工作中由于当时计算理论和硬件条件限制,诸多桩土相互作用分析都对地基模型进行线性简化处理,或利用二维模型进行简化分析。本文将采用大型通用数值分析平台ADINA,对横向荷载作用下的桩土相互作用进行三维数值模拟,分析其在水平荷载作用下桩顶的最大位移。然后根据API规范规定的P-y曲线,用非线性弹簧模拟桩土的相互作用,建立桩土相互作用的简化分析模型,将其在水平荷载作用下的桩顶位移与三维数值模型以及实际测定值之间进行比较,说明API规范规定的p-y曲线的适用性。将p-y曲线简化分析方法应用到大型桥梁的抗震分析中,在保证计算精度的前提下能大大减少计算量,具有非常重要的工程实际意义。
1 数值分析模型
本文采用ADINA中的摩尔一库伦材料模拟土体。库伦摩擦定律是土力学中的一个基本定律,按照这个定律,破坏面上剪切应力τf与法向应力σf之间满足下列关系式:
τf=c+σftanφ. (1)式中,c为黏聚力,φ为内摩擦角。
用摩尔应力圆表示,上述条件相当于破坏应力圆将与一条称为强度包线的直线相切。用主应力表示,式(1)可改写为将上述摩尔-库伦强度理论推广于塑性应变理论,即假定屈服条件也不受中主应力的影响。具有这种性质的材料称为摩尔-库伦材料(刘成宇,华祖馄,2009)。
三维桩土数值模型的参数设置如下:桩周土范围取桩半径的20倍,很多理论分析和计算结果证明了当桩周土范围足够大时其边界对桩身位移的影响非常小,因此取边界条件为:模型底部以及桩周土均采用全约束(袁志林等,2011)。
考虑到模型的对称性,只建立一半的真实模型,所有对称面在外法线上的位移是约束的,但在对称面上可以自由移动,采用对称约束,模型顶面上所有节点在各个方向上都是自由的。
本文使用试桩资料来自江苏镇江大港(1982)地区的试验(陈洪,2004),试桩基本资料如表1所示,地质资料如图1所示。
在模型中,桩体和土体采用8节点实体单元,用各项同性模型进行模拟。土体的变形包括弹性应变和塑性应变,是一种典型的弹塑性介质。土体的材料特性复杂、种类繁多,根据已知土体的不同参数,所对应的本构模型也有所不同,计算结果存在差异。因此模拟桩土间的相互作用时恰当地选取土体的本构模型,对于整个数值分析过程非常重要(李海林,2006)。目前应用比较多的是摩尔一库伦材料,在ADINA中用摩尔一库伦材料模拟土体,各个土层的属性根据图1中的各层地质资料进行输入。
在ADINA中通过建立接触对模拟桩土间的相互作用,首先在桩土界面上建立接触面,然后建立相互对应的接触对。接触对中接触面的选择需要满足一定的原则,即选择刚度大、自由度相对较少的面即桩表面为Target Surface,土体刚度较小自由度相对较多为Contaetor Surface。桩土之间的库伦摩擦系数取为0.2(周月慧等,2007)。建立的三维有限元模型如图2所示。
2 p-y曲线简化分析模型
根据API规范中规定的软粘土的p-y曲线公式,计算出单位桩长的极限土抗力为式中,y为由地面到深度z处的土的平均有效重度;cu为土的不排水抗剪强度;z为土的深度;d为桩的边宽或直径;J为实验系数,一般J=1/2,较硬的土取J=0.25。
土阻力达到极限土阻力一半时的相应变位为式中,y50为被动侧土达到极限水平抗力的一半时相应深度处桩的侧向变形(胡胜刚,2005);ε50为约一半的最大主应力差时的土的应变值,按表2取值。
桩径d计算值(徐鹏举等,2010)按下面方法求得:(1)圆形截面桩:实际桩径D>1m时,取d=0.9(1+D);实际桩径D≤1m时,取d=0.9(0.5+1.5D)。(2)方形截面桩:实际桩宽B>1m时,计算桩宽取d=B+1;实际桩宽B≤1m时,取d=1.5B+0.5。
由此确定p-y曲线为当y=8y50时,土达到p/pu=1的极限,此后保持为定值。软粘土的p-y曲线如图3所示。
根据计算出的p-y曲线,转化出力与位移之间关系的具体数值,输入ADINA中,生成非线性弹簧,模拟桩土之间的相互作用。
桩体采用二维梁单元模拟,桩底为固定约束,桩土之间的相互作用通过p-y曲线生成的非线性弹簧来模拟。模型总共设置了15个弹簧单元,在桩上节点与大地之间设置弹簧,计算模型如图4所示:
3 计算结果分析
3.1 P-y曲线对比分析
按照试桩试验的加载方式,在有限元计算中,同样施加49.0kN、98.0kN、147.1kN、196.1kN和245.2kN的横向水平荷载,计算得出桩顶水平位移。
由计算结果可知,三维数值分析模型计算的桩顶水平位移更接近实测位移,计算结果较p-y曲线简化分析模型计算得出的桩顶水平位移小。三维模型计算结果差异性产生的原因主要有:三维分析模型土体本构关系的选取与实际土体存在一定的差异,接触面相关参数的选取同样会影响计算结果。
镇江大港试桩在各级荷载作用下桩顶水平位移的实测值与三维数值模型和P-y曲线简化分析模型计算结果的比较如表3所示。镇江大港桩顶位移随水平力变化如图5所示。
随荷载的增大p-y曲线模型的计算结果误差也越来越大,造成这一结果的原因主要有:非线性弹簧模拟桩土间相互作用本身的近似性因素(李炜等,2011),同时所采用的P-y曲线是根据美国Austin地区的试验资料构造,应用到其他地区会存在一定的误差(曹维科,2011)。因此想要更好地应用p-y曲线简化模型模拟桩土之间相互作用,必须根据试桩所在地的地质资料,寻找适合本地区的p-y曲线。
3.2 桩身变形分析
桩受到横向荷载作用时,桩身的变形主要为水平向的挠曲。在不同水平向荷载作用下桩土相互作用的P-y曲线简化分析模型中桩身的水平位移沿埋深的变化如图6所示。由图6可知,随着荷载的逐渐增大桩身位移越来越大,荷载增大到一定程度之后,桩顶的位移增大幅度呈增长趋势。桩身位移沿埋深的变化充分说明了桩土之间相互作用的非线性,当荷载增到一定程度之后,桩逐渐达到极限状态,趋于破坏,桩顶位移急剧增大。
桩在49.0kN、147.1kN、245.2kN水平荷载作用下的桩身变形如图7所示,可以看出,桩顶位移随荷载的增大而增大,埋深达到15m后,桩身位移随荷载增大变化并不明显。桩身位移在桩顶处达到最大值,然后沿桩深逐渐减小,到桩体位移为零后,桩体位移开始反向增大,增大到一定值后又开始减小,到桩底时位移为零,很符合柔性长桩的特性(刘延芳,2014)。
4 结论
采用大型通用数值分析平台ADINA对水平荷载作用下桩基的工作性状进行分析,分别建立了横向荷载作用下的桩土相互作用三维有限元数值分析模型与p-y曲线简化分析模型。计算分析表明:
(1)三维有限元数值分析模型所得的计算结果与实际测量的结果基本一致,而应用API规范中规定的p-y曲线计算的桩顶位移与实测值之间相差较大,说明API规范中规定的p-y曲线有一定的局限性,只适用于与Austin地区地质情况大致相同的地区。
(2)p-y曲线模拟桩土间相互作用简化分析模型在不同水平荷载作用下的工作性状进行分析,计算结果与桩基实际受力性能基本一致,说明p-y曲线能较好地模拟桩土间的相互作用。这样,应用P-y曲线法须先根据本地区的地质资料由实验或者三维分析的方法求得适合本地区的p-y曲线。
(3)在保证计算精度的前提下,将P-y曲线模拟桩土间相互作用的简化计算方法应用到桩基抗震设计中能大大减少计算消耗,具有非常重要的工程现实意义。

