转换视角相对运动求最值

    朱向东 刘伟

    

    

    

    在初中数学图形与几何内容领域，图形的运动与变化是研究图形的有力工具，通过学习物理学，我们知道，静止与运动两者都是相对的概念，与物体相对于选定的参照物有关，当一列火车经过车站时。我们就说这列火车相对车站而运动，但是对在火车上的旅客，可以认为车站是在与火车运行相反的方向相对火车而运动，所以，在描述物体是否运动时，观察者必须选择一个参照物，然后根据所选定的参照物来确定物体是否运动，受此启发，在数学学科中，如果我们转换视角，从相对运动的角度来看待图形的运动与变化，是否会产生奇妙的效果？下面，笔者就以教学实践中学生理解较为困难的最小值问题为例谈谈自己的想法，敬请指正。

    1 原题呈现

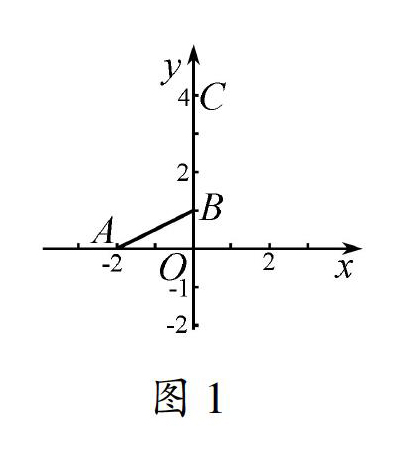
    如图l，在平面直角坐标系xOy中，点A（-2.O），B（0.1），C（0.4），将线段AB向右平移，在平移过程中，AC+BC的最小值是____，

    学生熟悉的往往是牵涉一个动点的问题，因为此问题中有两个动点：A和B，所以学生感到束手无策，产生思维障碍，不知从何人手。

    2 一般思考

    以上解法源于对平移型将军饮马图形的理解和把握，虽然问题中有两个动点，但是当把点B向下平移一个单位再向左平移两个单位就可以得到点A'，所以，如图3.将点B'连同它所在的线段B'C一同向下平移一个单位再向左平移两个单位至A'C'，问题就可转化为求A'C+A'C'的最小值，其中，点C，C'不动，只有点A'在动，且点A'在直线AO上运动，通过平移，研究两个动点的问题最终转化为研究一个动点的问题，原问题转化为典型的將军饮马问题，同样，也可以将图2中的A'C向右平移两个单位再向上平移一个单位，使A'与B'重合，

    但是在实际教学中我们发现，在上述探索的过程中，确实仍有相当一部分同学表示感到理解比较困难，难以掌握，自然也就谈不上能举一反三了。

    3 转换视角

    怎样才能让学生更好地理解呢？受物理学的启发，如果从相对运动的角度看，思维难点则可以很轻松的突破，可作如下的思考：本题要求“点C不动，线段AB向右平移”，相当于“线段AB不动，点C向左平移”，当然，二者平移的距离相同，即原问题可转化为下面的新问题：如图5.将点C向左平移，在平移的过程中，求AC+BC的最小值，此为典型的将军饮马问题，学生很熟悉，只需作点B关于射线CD的对称点B'，线段AB'的长就是所求的最小值，易

    4 类比拓展