从一道几何名题到中考模拟试题的演变
张安军
在数学历史的发展中。有一些耐人寻味的经典名题,如璀璨的明珠,吸引了一代又一代的数学爱好者,同时也得到广大数学命题者的青睐,试题命制者通过对一些名题的挖掘和改编,选择了合适的内容作为试题的考查对象,以经典名题为背景的试题。让数学试卷充满浓浓的文化味。又能激发学生探索数学的热情,提升素养,把握数学的本质,笔者受区教学发展中心委托,命制一份区中考模拟试题,在命制过程中,对历史上一道经典的几何名题进行挖掘和开发。演变成了一道几何压轴题,现展示其命制过程,与同行们分享。
1几何名题及其分析
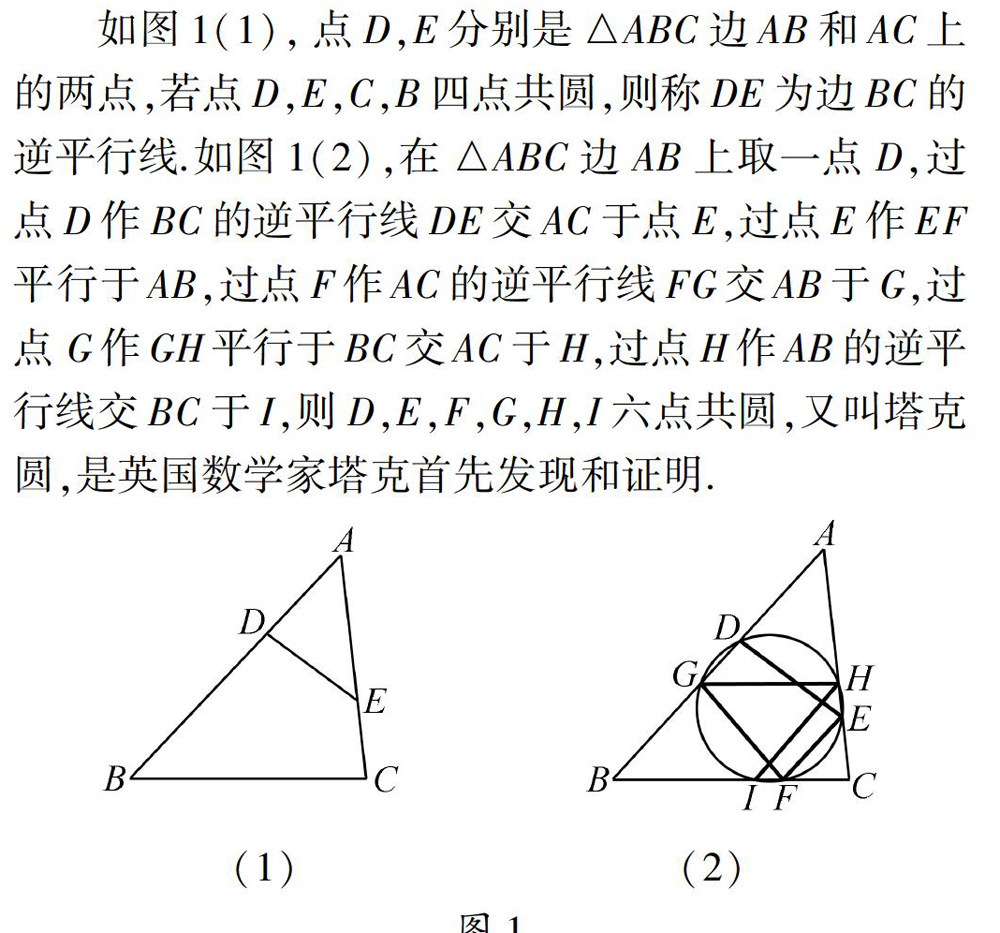
英国数学家塔克给出“逆平行线”的概念。“逆平行线”不同于“平行线”。但又和“平行线”有着密切的关系,两条直线平行它们所构成的同位角、内错角相等,反之若两条直线被第三条直线所截,所构成的同位角或内错角相等,那么这两条直线平行,在一个三角形中。若一条直线截三角形的两边所构成的四边形恰好有一个外接圆,那么该截线称作三角形第三条边上的“逆平行线”。圆的内接四边形的一个外角等于内对角,实质上借助了角的数量关系,在平行线的基础上命名“逆平行线”。三角形各边上的逆平行线(或平行线)与三角形各边相交构成六个点。如果以此为背景,直接作为考题,证明这六个点共圆,不是很妥,《数学课程标准(2011年版)》(以下简称“课标”)对判断四点共圆不作要求。另外整个图形线条繁琐。背景复杂,起点高,不利于不同层次的考查和区分,然而“逆平行线”内涵丰富,揭示了角与角之间的数量关系,与初中的三角形、相似三角形、圆内接四边形都有着直接的联系。“逆平行线”这一名称也是基于学生的最近发展区而提出。
2试题命制过程
塔克圆中最鲜活的素材就是“逆平行线”。由于“逆平行线”是初中教材中没有出现的一个名词。因此可以命制一道新定义试题,这样的新定义源于历史,而不是命题者为编制试题随意编造一个新名词,以“定义——理解——探究——应用”命题思路展开。先定义“逆平行线”,在理解定义的基础上,考查从定义出发判断一条线段是否为“逆平行线”。结合新定义用尺规作图求作“逆平行线”,然后在特殊的三角形中运用新定义进行自主探究解决问题,命制时,为了突显试题的整体性和连贯性,以“逆平行线”为主线。贯穿问题的始终。
初稿如图2(1),点D,E分别是△ABC边AB和AC上的点,若∠B=∠AED,称DE为边BC的逆平行线。
(1)如图2(1),点D,E分别是△ABC边AB和AC上的点,若AD=3.AB=8.AE=4.AC=6.求证:DE是△ABC边BC的逆平行线,
(2)在(1)的条件下,过点E作边AB的逆平行线交BC于F,请用尺规作图求作EF,
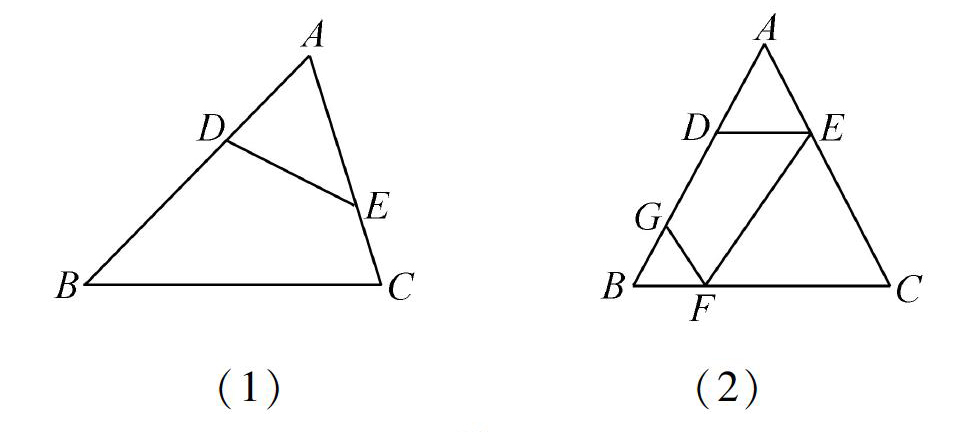
(3)如图2(2),已知等腰△ABC,AB=AC,D是边AB上的一点。过点D作边BC的逆平行线交AC于点E,过点E作边AB的逆平行线交BC于点F,再过点F
分析:定义“逆平行线”不够严谨,缺乏一般性,第(1)问,为了考查对定义中“逆平行线”的理解,给出了太多的数据,这些数据对后继的问题缺乏关联性;第(2)问在理解“逆平行线”的基础上,过一点作已知直线的“逆平行线”。重在考查几何尺规作图,然而在几何新图形学习的过程中,如三角形等,一般地是先确定研究对象(给出定义)再探究它的性质(发现,证明),那么“逆平行线”是否有特殊的性质呢?第(3)问,结论已知,探索条件,重在考查等腰三角形、全等三角形等相关知识,由于探索的结论指向过于明显。作为压轴题,综合难度不够,也没有突出初中数学核心素养的考查,通过上述分析。“逆平行线”定义的严谨性和一般性有待加强,第(1)问人为的拼凑明显,不够自然,第(2)问没有突显几何图形学习的一般观念,即确定研究对象(给出定义)→性质(发现,证明)→图形的判定→研究特例,第(3)问在难度上有待加强,
通过上述分析,在一般三角形中不易探索逆平行线的性质,若三角形变为等腰三角形,“逆平行线”有哪些性质呢?容易发现“逆平行线”的相关性质,如过等腰三角形其中一腰上的点作底边上“平行线”。这一条“平行线”也是一条“逆平行线”。同时还发现这条“逆平行线”垂直于外心与三角形顶点的连线。这两条性质在画“平行线”的过程中自然产生。这样就可以构成试题的两个问,然后从定性到定量。让学生在具体的等腰三角形中继续进行探索“逆平行线”的性质。“逆平行线”所围成的四边形有无面积最大值,四边形最大时,G,D两点有何位置关系?这样就形成二稿,
二稿用一条直线截三角形的两边,所截得的四边形若对角互补。则称该直线为三角形第三条边的逆平行线,如图3(1),已知△ABC中,AB=AC,过边AC上的点D作DE//BC交BC于点E。
(1)求证:DE是边BC的逆平行线,
(2)如图3(2),EF为边AB的逆平行线,点O,I分别是△ABC的外心和内心。连接AO和AI,可得AO⊥DE,AI⊥DE,若连接CO,CI,一定与EF垂直的线段是哪一条。并加以说明。
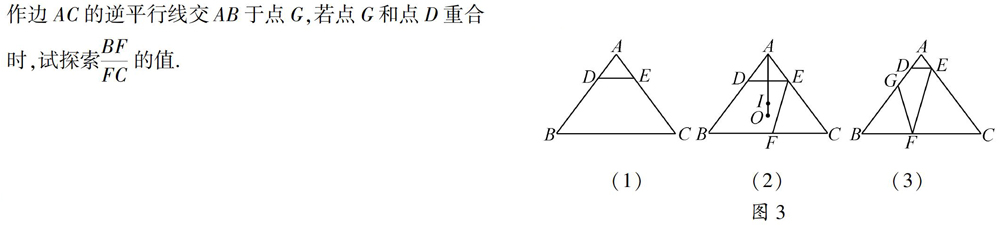
(3)如图3(3),已知AB=5.BC=6.过点E作边AB的逆平行线。交BC于点F,过点F作边AC的逆平行线,交AB于点G设AD=x,S四邊形AEFG=y,
①求y关于x的函数解析式及其自变量取值范围,并求y的最大值。
②当y最大值时,试探索AD+BG与AB的数量关系,
分析:虽然“逆平行线”的定义较以前严谨,也突显了一般性,但是仅用文字语言进行定义的界定,对数学成绩基础不好的同学在理解定义上会带来困难。这样在理解定义上缺乏公平性,第(1)问过腰上的一点作底边的平行线,难度适中,叙述简洁,在特殊的三角形中“逆平行线”和“平行线”是相同的,第(2)问引导学生从特殊到一般,主要考查提出和发现问题,并同时对自己所提出的问题加以证明,然而通过类比。特意的引导和铺设,会降低整道试题的难度,第(3)问从定性到定量的刻画,揉合了等腰三角形、勾股定理、相似三角形、二次函数等初中数学核心知识,然而在语言上叙述略显繁琐。能否使整个问题变得简洁明了呢?带着这样的问题再进行命制探索,
在定义“逆平行线”后。再通过图形加以说明。让不同层次的学生都能理解“逆平行线”的定义。突显试题的效度和信度,考虑压轴题有一定的区分度,增加第(2)问的难度,删除了等腰三角形顶角角平分线与“逆平行线”有关“垂直”这一性质的暗示,将这一结论隐藏起来,让学生自己发现结论,为了使第(3)问叙述变得简洁,题意清晰,把条件都移到题干上,通过细细研磨,图形美观,问题呈现简洁,设问层次分明,
定稿用一条直线截三角形的两边。若所截得的四边形对角互补,则称该直线为三角形第三条边的逆平行线,如图4(1),DE为△ABC的截线,截得四边形BCED。若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线。
如图4(2),已知△ABC中,AB=AC,过边AB上的点D作DE//BC交AC于点E,过点E作边AB的逆平行线EF。交边BC于点F。
3 几何名题到试题演变的思考
本题以“逆平行线”为主线构造探究题。试题以新定义的方式呈现,叙述简洁,内涵丰富,巧妙地将等腰三角形、勾股定理、圆心角定理、平行线、相似三角形、二次函数等初中数学的核心知识融合起来。同时设计的探究内容遵循“简单到复杂、特殊到一般”的规律,是一道具有较好的区分度和效度的新定义型试题。得到了一线教师的广泛好评,回顾本题的命题过程。从最初的立意到后续的试题成型,有许多感悟值得笔者在今后的命题中鞭策自己。现整理分享如下,
3.1 几何名题的改编要突出数学的核心概念和知识
历史上数学名题是许多数学家历经多年精心研究的成果,直接搬迁作为试题,特别是关键性的压轴题有许多不妥。如上述中数学名题塔克圆和三角形九点共圆定理等。用到的许多数学知识在“课标”中不作要求,如四点共圆的判定定理等;也有的作为选学内容。如垂径定理等,同时历史上数学名题都有一定的难度,直接作为试题,不利于不同层次学生的考查,因此从数学名题走向试题需要酝酿和发酵的过程。命制者根据数学名题的材料对考查的目标重新进行构造。所考查的内容应是初中数学的主干知识。不得超越“课标”。也不得通过新定义的方式把高中的知识下放到初中。避免加重学生学业负担,例如上述试题命制时虽取自于塔克圆。但所考查的内容避免了“六点共圆”的繁琐,在“六点共圆”的材料中取出一条线,即“逆平行线”。然后通过对“逆平行线”在特殊的三角形中展开研究,在研究的过程中既涉及到初中的主干知识,又突显对数学能力的考查,让数学核心素养的考查落地生根,
3.2 几何名题的改编要体现自然流畅的表达
从几何名题走向试题要基于学生的认知,新概念要基于学生的最近发展区内提出。在名题改编时要深入挖掘数学名题所蕴含的思维资源。要以与学生智力发展水平相适应的方式,有层次、有梯度的表达出来,这样才能有效地发挥数学名题的育人价值,
例如上述试题中“逆平行线”的提出基于学生已有的“平行线”概念。在问题的设置上类比三角形的“平行线”,如图5(1),过△ABC边AB上一点D作BC的平行线交AC于点E,过点E作AB平行线EF交BC于点F,再过点F作AC的平行线交AB于点G,这样得到三条平行线,一般地点G与点D不重合,如图5(2),特殊情形当点D是边AB的中点时,点G与点D重合,此时这三条平行线组成三角形的中位线。三条中位线所构成的三角形的面积是原三角形的面积的四分之一,那么三角形的“逆平行线”也有相类似性质吗?
试题以“逆平行线”为主线。让学生展开类似性质探究,在最后的一个问题中,AD在何位置时,点D和G点重合。让学生进行自主探究,整个问题的设置由易到难,梯度合理,各问之间既要相对独立,又要相互关联。学生的思维始终在探究“逆平行线”的主线上,承接问题很好地兼顾两头。每一个问题都和下面的问题相关。既推动学生的思维向纵深发展。问题和问题又相互关联,
3.3 几何名题的改编要突显探究的意义和价值
数学经典问题或名题有的是因为好玩或美学价值等激发一代又一代人去研究和探索。例如爱因斯坦说:“在12岁时,我经历了另一种性质完全不同的惊奇,就是在一个学年的开始时,当我得到一本关于欧几里德平面几何的小书时所经历的。这本书里有许多断言,比如,三角形的三个高交于一点,它们本身虽然不是显而易见的,但是可以很可靠地加以证明,以至任何怀疑似乎都不可能,这种明晰性和可靠性给我造成了一种难以想象的印象……”。爱因斯坦被三角形的三条高线交于一点所震撼。激起他对数学的探究的热情,因此从数学名题到试题的演变也要让学生体会到数学的文化價值和广泛的应用价值。同时也让学生学会用数学思维解决问题,感受到数学家积极探索和追求真理的精神,在上述命题中。英国数学家塔克提出“逆平行线”。命制者借助已有的名称。构建新概念,然后和“平行线”进行比较,在一个三角形中有没有既是“平行线”又是“逆平行线”呢?让学生在特殊的三角形中进行验证,其次在等腰三角形中,发现等腰三角形的顶点和外心的连线垂直于两腰上的“逆平行线”,那么这一性质不在两腰上的“逆平行线”还成立吗?更一般地,对于任意三角形的外心和顶点的连线都垂直于“逆平行线”吗?在等腰三角形中过其中边上的一点依次作“逆平行线”,存在特殊时刻的位置,三条“逆平行线”可组成一个三角形,那么更一般地这一规律还成立吗?“逆平行线”的性质让学有余力的学生引申到课外继续探索。在对比和关联中感受到问题探究的意义和必要性。

