基于学科学习力的数学课程结构

【摘要】人才发展模式的变革等背景，都彰显了培养学生学习力的迫切性.学习力的具体价值主要包括能够改进学生的学习行为和构建基于学生学习的教学方式等.学习力可以理解为学生的生长力，对它可构建三层次六要素结构模型.数学学科学习力由一般学习力和数学学科特有的学习力（由數学学习能力、数学能力和数学创新能力等成分组成）两部分组成.并在介绍浙江省相关数学课程的基础上，进行基于数学学习力的课程结构构建和实践应用.最后给出数学教育应多元化发展、抵制考试和考试文化的过度影响以及“指向数学学习力的数学课程结构”的实践应用等进一步思考.
【关键词】 学习力；数学学科；数学课程
在信息社会的全球背景下，学习者的学习需求也正在不断丰富，然而现代公民是否具备足够的素质来适应瞬息万变的社会发展呢？这就对我们教育者提出了新的要求，即如何在学校学科教育中为学生提供合适的学科课程，提升学生学习力.人才发展模式的变革、传统教与学的困境以及新课程改革的迫切要求，都彰显了培养学生学习力的迫切性.学习力的具体价值主要包括能够促进学生的发展、改进学生的学习行为和构建基于学生学习的教学方式.
笔者在《数学学科学习力的要素及模型构建》[1]一文中论述了数学学科学习力的要素，并初步构建了数学学科学习力的模型.在此基础上，本文进一步对基于数学学科学习力的数学课程结构进行论述.
1 学习力及数学学科学习力
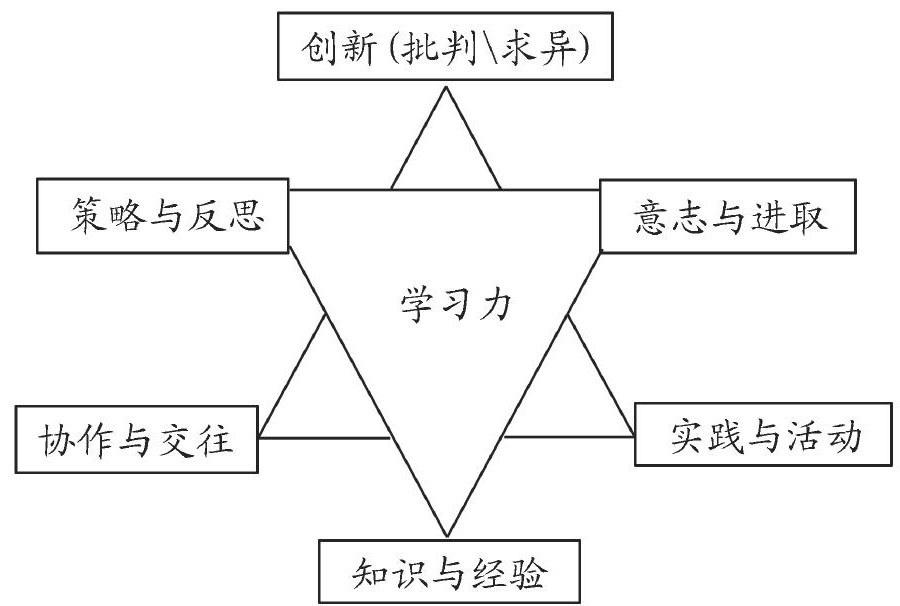
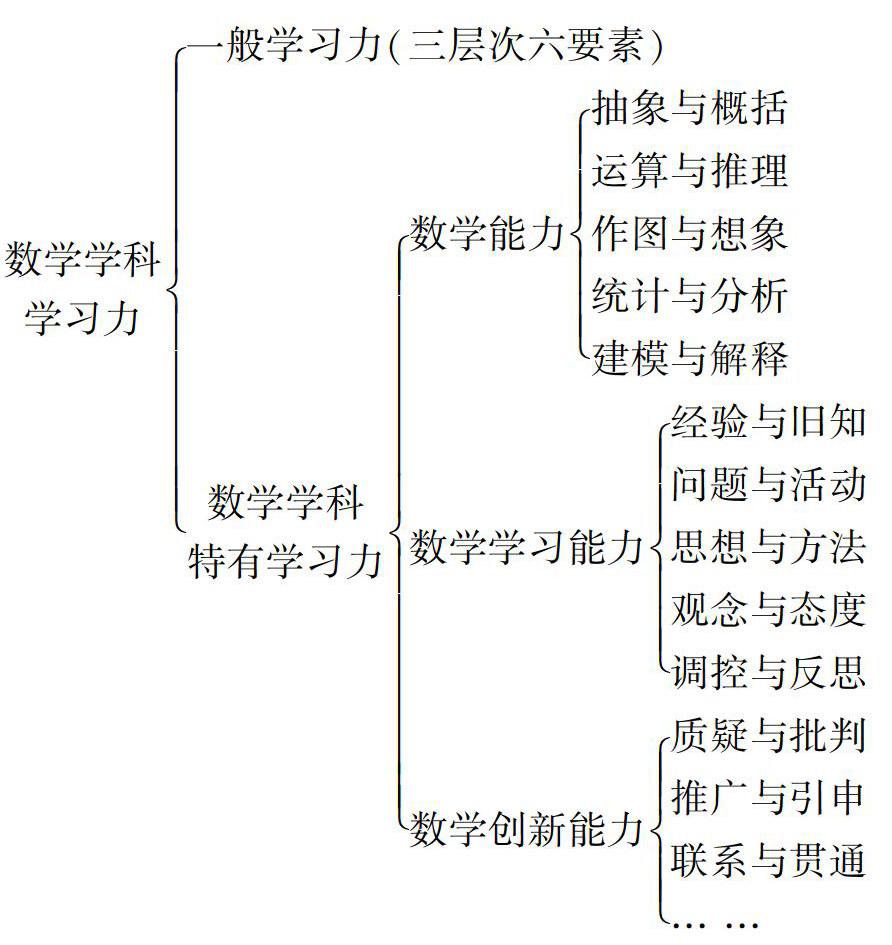
“学习力”一词最早来源于管理学领域，多以“组织学习力”、“学习型组织”出现，它反映了组织作为一个整体对各种内外信息的认知与反应的能力[2].以学习力、学习能力、learning power、learning ability、learning capacity等为关键词搜索相关文献后发现，对学习力理论的系统研究主要以国外文献为主，尤其英国相关较为突出；而国内文献较少，目前还没有形成系统研究.学术界普遍认为学习力是一种综合的、复杂的能力，研究主要围绕概念、内涵、构成要素、应用（提升策略等）进行.裴娣娜教授及其研究团队分析、提取出学习力六大要素[3]，它们分别是：知识与经验、策略与反思、意志与进取、实践与活动、协作与交往、批判与创新；并提出了学习力的三层次六要素结构模型（如图1所示）.图1学习力的三层次六要素结构模型数学研究的对象是数量关系和空间形式，数学的运作在于“思维”，人脑对数学对象的思考是思维运作.数学教学是数学思维活动的学与教.数学教学的关键之一是处理好理解与记忆之间的关系，特别是，理解应当被看成熟练掌握各种算法的一个必要前提.数学学科学习力的核心是思维、数学思维，提升学习力，就是促进学生数学思维的发展.而数学学科学习力由一般学习力和数学学科特有的学习力两部分组成，其中数学学科特有的学习力又由数学学习能力、数学能力和数学创新能力等成分组成.
数学能力包含很多内容，在数学学科课程中，需要重点培养学生抽象与概括、运算与推理、作图与想象、统计与分析、建模与解释等五组能力（学科核心素养）.数学学习能力主要包括经验与旧知、问题与活动、思想与方法、观念与态度、调控与反思等五组内容.数学创新能力的成分有质疑与批判、推广与引申、联系与贯通等.
2数学课程结构的构建
为贯彻落实《国家中长期教育改革和发展规划纲要》，优化育人模式，推进普通高中特色化多样化发展，提高普通高中教育质量和办学水平，加快教育现代化建设，浙江省制定了深化普通高中课程改革方案，并于2012年秋季在全省普通高中全面实施，主要内容可以概括为“调结构、减总量、优方法、改评价、创条件”，为“普通高中分层走班，学生自主选课”创造了有利条件.同时作为全国两个高考综合改革试点之一，浙江省于2014年9月19日发布了“新高考方案”，将采用统一高考招生、高职自主招生、单独考试招生、“三位一体”招生等四种模式，考生可根据实际情况，从中选择适合自己的模式.该方案将从2014年秋季新入学的高一学生开始实施.在此背景下，浙江省各个普通高中积极探索学校课程的顶层设计，以及具体的教学安排.
2.1基于数学思维的课程分层分类
学校课程需要有一个顶层设计，在此之下，各学科课程结构体系需有一个核心主题词.同一学科，不同学校可有不同的主题词.比如，数学学科课程结构可用数学思维作为统领，进行分层分类、纵横交错搭建数学课程结构.
其中的“分层”，具体可分为三层：（1）基础课程：针对学困生和一般学生，注重数学思维引领；（2）荣誉课程：针对中等生，注重数学思维提升；（3）挑战课程：针对资优生，注重数学思维突破.此外，可针对基础特别差的学困生，还可以设计辅弱课程（或称为补差课程），注重数学思维体验，作为第四层.
其中的“分类”，具体可分为三类：（1）基础类课程：面向全体学生，主要关注知识基础，当然也有思想方法的基础，注重扎实度，注重数学思维引领；（2）拓展类课程：面向部分学生，主要关注思维的拓展，当然也有知识的拓展，注重广度，注重数学思维提升；（3）研究、特长类课程：面向个体学生，主要关注能力的提升，注重高度和深度，注重数学思维突破.
还可以有不同的分类，比如按照学生生涯规划方向，分为理工方向、社会方向、人文方向和艺术方向等类，分别提供不同的数学选修课程.
2.2基于数学学习力的课程结构构建和实践应用
基于课程改革的背景，为了发展学生的数学思维，提升学生的数学学习力，基于数学学习力的课程结构构建亟待进行.除了教育部门规定的必修课程和限定先修课外，我们还需给学生提供多种选修课程.同时，基于数学学习力的课程结构构建需要从不同认知水平学生、课程类别和课程指向等三个维度进行构建，可构成3×3×3共27个课程定位的课程结构.第1维“学生水平”维度，可分为学困生、中等生和资优生等3类学生；第2维“课程类别”维度，可分为基础类、拓展类和研究类等3类课程；第3维“能力指向”维度，可分为指向数学学习能力、数学能力和数学创新能力等数学学习力要素的3类课程.
第1维主要影响课程内容的难易，第2维主要影响课程内容的属性，第3维主要影响课程内容的目标.基于数学学习力的课程结构构建，关键在于第3维，以下就第3维“课程指向”维度进行展开说明.
指向数学学习能力的课程，也就是指向学生经验与旧知、问题与活动、思想与方法、调控与反思、观念与态度等五组学习能力培养的数学课程.指向学生经验与旧知、问题与活动方面，例如《数学与生活》（《生活中的数学》）、《数学软件应用》等课程；指向学生思想与方法、调控与反思方面，例如《高中数学学习方法指导》、《数学思维方法》等课程；指向学生观念与态度方面，例如《数学文化》、《民俗数学》等课程.
指向数学能力的课程，也就是指向学生抽象与概括、运算与推理、作图与想象、统计与分析、建模与解释等五组能力培养的数学课程.指向学生抽象与概括、运算与推理方面，例如《组合数学》、《数学思维训练》等课程；指向学生作图与想象方面，例如《数学与建筑》、《数学与工艺美术设计》、《数学与模具制作》等课程；指向学生统计与分析、建模与解释方面，例如《统计初步》、《数学建模》等课程.
指向数学创新能力的课程，也就是指向质疑与批判、推广与引申、联系与贯通等能力的数学课程.指向学生质疑与批判方面，例如《数学悖论》等课程；指向学生推广与引申方面，例如《初等数学研究》等课程；指向学生联系与贯通方面，例如《数学论文写作》等课程.
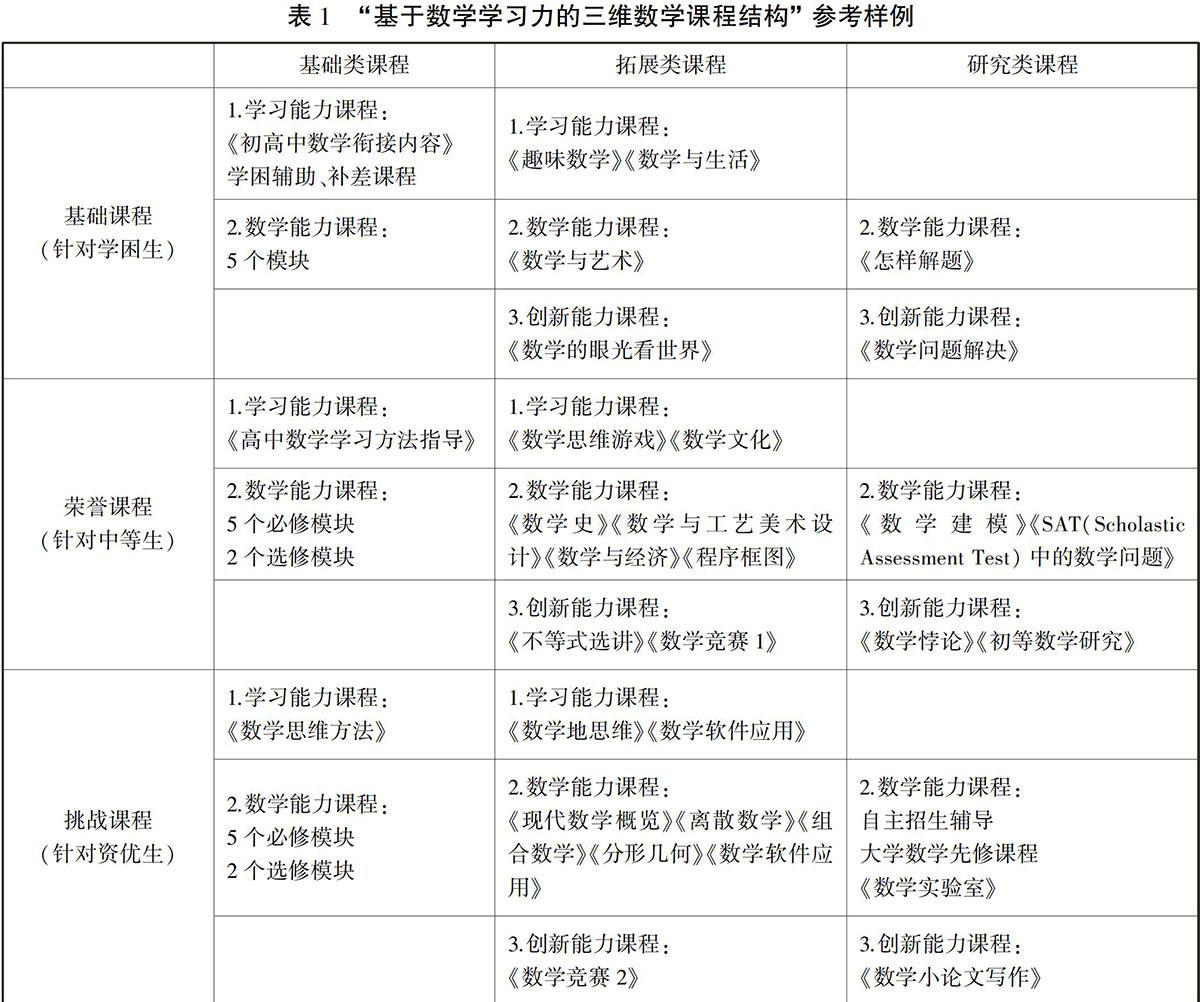
对于第1维和第2维进行横纵分列，将第3维进行内部渗透，可搭建出“基于数学学习力的三维数学课程结构”参考（如下表1）.表1“基于数学学习力的三维数学课程结构”参考样例
基础类课程拓展类课程研究类课程基础课程
（针对学困生）1.学习能力课程：
《初高中数学衔接内容》
学困辅助、补差课程1.学习能力课程：
《趣味数学》《数学与生活》2.数学能力课程：
5个模块2.数学能力课程：
《数学与艺术》2.数学能力课程：
《怎样解题》3.创新能力课程：
《数学的眼光看世界》3.创新能力课程：
《数学问题解决》荣誉课程
（针对中等生）1.学习能力课程：
《高中数学学习方法指导》1.学习能力课程：
《数学思维游戏》《数学文化》2.数学能力课程：
5个必修模块
2个选修模块2.数学能力课程：
《数学史》《数学与工艺美术设计》《数学与经济》《程序框图》2.数学能力课程：
《数学建模》《SAT（Scholastic Assessment Test）中的数学问题》3.创新能力课程：
《不等式选讲》《数学竞赛1》3.创新能力课程：
《数学悖论》《初等数学研究》挑战课程
（针对资优生）1.学习能力课程：
《数学思维方法》1.学习能力课程：
《数学地思维》《数学软件应用》2.数学能力课程：
5个必修模块
2个选修模块2.数学能力课程：
《现代数学概览》《离散数学》《组合数学》《分形几何》《数学软件应用》2.数学能力课程：
自主招生辅导
大学数学先修课程
《数学实验室》3.创新能力课程：
《数学竞赛2》3.创新能力课程：
《数学小论文写作》注：
① 浙江省规定5个必修模块分别是数学1、数学2、数学4、数学5和选修2-1，2个限定选修模块是选修2-2和选修2-3.基础课程/基础类课程中的“5个模块”可以是5个必修模块，或者是5个必修模块和2个选修模块中选择其中5个，也可以从5个必修模块和2个选修模块中选择章节，重组成5个模块.
② 基础类课程不设指向创新能力的课程，研究类课程不设指向学习能力的课程.
③《数学竞赛2》比《数学竞赛1》难度大.由此可知，其他课程我们也可根据难度分为1、2、3三种（层）课程.
④ 高一水平的学生可以选择下一层级的拓展类课程和研究类课程.也不禁止低选高.
⑤ 表中只列了部分课程名称.
3进一步的思考
3.1学教育应多元化发展
在全面实施素质教育和提高全民族的科学文化素质为宗旨的新课程改革中，我们的基础教育应当走出精英化误区[4].在新课程改革中，着眼于未来人才的教育培养，应该清晰地认识未来社会的多元化需求.未来社会是知识经济高速发展的多元化时代，亟需的是具有较强学习力的多元化创新人才.数学教育应该多元化发展，在学校教育以及学科教学中，应该时刻秉承这一思想.以培养学生学习力为首要任务，培养多元化具有数学学习力的学生（数学成绩不一定要好），让学生有潜力成为未来社会某个领域（也可以是文科领域）中的人才.
3.2抵制考试和考试文化的过度影响
中国传统的考试及考试文化不可避免地将对课程改革或多或少有影响.现在迫切需要做的不是围绕这个作无意义的争论，真正需要做的是，要从复杂理论与中国传统文化等复杂方面去推进课程改革，使之向前不断迈进[5].学科课程是培养学生学习力的土壤，在实践的过程中应该防止形似主义、功利主义对课程实施的错误导向，而应引导学生对待学习、对待成败有正确向上的价值观.但与此同时，也要注意是对考试和考试文化的过度影响部分进行抵制，而不是走向另一个极端.毕竟能在考试中发挥出自己应有的水平也是一种素质，尤其是走出校园，走向社会，毕业生还是要面对多种“考试”.
3.3“指向数学学习力的数学课程结构”的实践应用
“指向数学学习力的数学课程结构”参考，主要提供的是数学课程顶层设计的框架参考.具体实践过程中，学校可以按照各自的实际情况来构建适合学生发展的校本化的“指向数学学习力的数学课程结构”.第一步，主要是要将学校实际已开展的选修课程（尤其是比较优秀的课程）融入到“指向数学学习力的数学课程结构”中；第二步，主要是要针对课程结构中没有涉及到的课程模块进行课程开发，或者进行相关课程的转化；第三步，主要是要对于课程结构中某些课程过多的课程模块进行优胜劣汰.在实践中，我们还有很多工作要去做.
（致谢：本文在写作过程中，同事张维忠教授、杨光伟副教授、唐恒钧博士、陈碧芬博士参与了讨论，并提供了建设性意见；研究生陆吉健、刘曌查阅了相关文献，并协助写作.在此表示谢意.）
参考文献
[1]朱哲.数学学科学习力的要素及模型构建[J].中学数学杂志，2017（7）：1-5.
[2]A. K. Yeung ， D. O. Ulrieh ， S. W. Nason and M.A. Von Glinow .Organizational Learning Capability ： Generating Ideas with Impact [M].Oxford University Press，1999.
[3]裴娣娜.學习力： 诠释学生学习与发展的新视野[J].课程·教材·教法， 2016， 36（7）： 3-9.
[4]杨启亮.关怀普及：淡化教育教学实践中的精英化取向[J].教育研究， 2003（9）：69.
[5]韦东余，焦方瑞，尚金兰.理解课程改革的复杂性——“中国传统文化、复杂理论与课程改革国际讨论会”综述[J].全球教育展望， 2010（12）：93.