2013年芦山MS7.0地震余震序列震源机制一致性的时空变化
段云歌 陈天长 苏金蓉 雷建设 唐琳 吴朋


摘要:利用体波谱振幅相关系数分析方法,对2013年4月20日至6月30日芦山MS7.0地震余震序列中四川地震台网固定台站记录的ML2.0~4.0地震的震源机制一致性进行了研究。将主要研究区分为5个子区,分区计算震群的平均相关系数。结果显示,同一时段内,震后2区平均相关系数最高,达0.809,随着与该区距离的增大而逐渐减小。4区2013年6月平均相关系数最低,仅为0.524;整个研究区的总平均相关系数由0.785变至0.575。主震发生后,随着时间的推移,各子区内地震的平均相关系数均逐渐减小;随着区域应力场能量的释放,震群的震源机制一致性逐渐变差。
关键词:芦山MS7.0地震;余震序列;谱振幅相关系数;震源机制一致性
中图分类号:P315.7 文献标识码:A 文章编号:1000-0666(2018)02-0251-07
0 引言
震源机制解描述了震源的几何特性,反映了地震破裂的运动学特征,是研究区域构造应力的基础。地震学的发展和数字记录的应用使震源机制的研究进入了新的阶段,目前有多种测定震源机制解的方法,如P波初动法、地震矩张量反演等。其中大多数方法对地震观测台站的记录数有较高的要求,目前由于受台网布局和观测点密度的制约,大量中小地震、尤其是小地震的台站记录数往往很有限,很难用P波初动等方法求出可靠的震源机制解,因此,直接求解小震震群中单个地震的震源机制解存在较大的困难。
对较大地震的前震与余震的波形进行研究,得到地震前后震源机制的变化过程,历来是地震预测研究关注的问题(刘泽民等,2010;付虹等,2011;泽仁志玛等,2009)。筹В?978)根据海城前震序列的研究,提出用震源机制的一致性作为判别前震的新参数;崔子健等(2012)认为谱振幅相关分析法可能是判定小震群类型的物理意义较为明确的方法,且具有实用价值;程万正等(2006)对川滇地区4个次级地块上的925次地震进行震源机制解一致性分析,通过对次级地块大量区域小震震源机制解的测定,给出了应力场变化信息。前震序列、余震序列‘震源机制的变化过程存在规律性,具有重要的地震前兆意义(国家地震局监测预防司,1997)。因此,对中小地震震源机制解进行综合分析,就有可能捕捉到与强震发生有关的应力场变化信息。朱航等(2006)曾提出了一种方法,即采用体彼谱振幅相关系数来研究地震序列中震源机制是否相似,该方法给出的不是单个地震的震源机制解,而是地震序列震源机制一致性的变化特征。
2013年4月20日8时2分,四川芦山发生MS7.0强震,根据中国地震台网中心测定,震中位置为(30.3°N,103.0°E),震源深度17km。主震后随着余震的发生,地壳内部能量得以释放,区域应力场也随之发生一些变化,本文利用体波谱振幅相关方法分析芦山MS7.0地震余震相关系数的变化规律,从震源机制一致性的变化中探讨芦山地区的区域应力变化情况。
1 基本原理及计算方法
在地震学中,台站j记录第i个地震波位移的谱振幅可表示为:
Ouj(f)=Mi(f)·Rij(θ,φ)·Pij(r)·Fij(f,r)·Gj(f)·Ij(f)(1)式中:f表示频率;r表示地震与台站之间的距离;Mi(f)是震源谱;Rij(θ,φ)為辐射图型因子;θ、φ表示地震到台站的方位角和离源角;Pij(r)是几何扩展系数,仅与距离相关;Fij(f,r)是地震波的衰减项;Ij(f)是仪器响应,Gj(f)是场地响应。其中,Mi(f)的表达式为:式中:M0为地震矩,fc为拐角频率。
如果2次地震(a,b)震源位置相同,或者2次地震震源之间的距离远小于地震到台站之间的距离,那么这2个地震到同一个台站的几何扩散、非弹性衰减、仪器响应和场地响应是一样的。对于同一频率,在同一个台站上2次地震事件的观测谱值之比可表示为:当f≤fc时,式(3)可表达为:式中:Oaj(f0)和Obj(f0)表示2个台站观测谱的零频谱值;
由式(4)可知,对于发生在同一震源区的2个地震,在同一个台站的零频观测谱值之比与其辐射图型因子之比线性相关,而辐射图型因子取决于震源机制解的几何特性(走向、倾角和滑动角)。可以推知,对同一震源区的不同地震在不同台站得到的零频观测谱值进行比较,应该可以得到不同地震之间的震源机制差异。
Lund和Boovarson(2002)提出一种计算体波谱振幅相关性的方法,即对同一震源区2次事件在相同台站的波形记录,使用直达P、S波的零频谱振幅值计算相关系数。
对于3分向地震波形记录,经过旋转每个台站可以得到5个零频谱值:垂向和径向P波(PZ和PR),垂向、径向和切向S波(SZ、SR和ST),称这5个谱值为谱值分量。根据台站和震中位置,计算台站在震源球上的方位角。然后根据地震与台站间的方位角,对台站记录的2个水平分量进行旋转,得到径向和切向分量:
R(t)=N(t)cos(Az)+EN、sin(Az) (5)
T(t)=-N(t)sin(Az)+E(t)cos(Az)式中:R(t)和T(t)表示径向和切向分量;N(t)和E(t)表示南北和东西分量记录;Az表示方位角。
2 资料选取及初步分析
2013年4月20日芦山MS7.0地震后,发生了大量余震,截至2013年6月30日,四川地震台网共记录到余震近万次。本文选取2013年4月20日至6月30日震中空间分布相对集中的1129次ML2.0~4.0地震序列做为研究对象。
由于研究区(30.1°~30.4°N,102.8°~103.1°E)范围较大,故将主要研究区划分为5个子区分别进行计算(图1),分别是1区(30.1°~30.2°N,102.8°~102.9°E)、2区(30.2°~30.3°N,102.8°~102.9°E)、3区(30.2°~30.3°N,102.9°~103.0°E)、4区(30.3°~30.4°N,102.9°~103.0°E)、5区(30.3°~30.4°N,103.0°~103.1°E)。这样,每个子区控制在经纬度0.1°左右的范围内(约11km×11km),分区后,每个子区内小震群相对于所选台站来看,可理想地看作是一个点。芦山地震主震震中位于3区内。
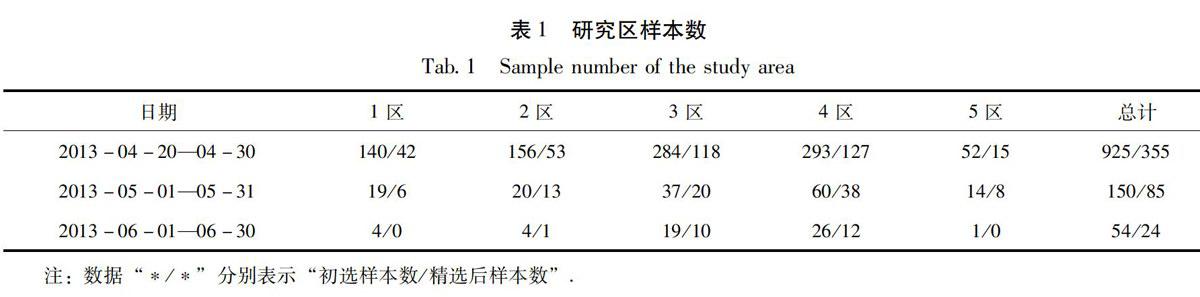
对所选余震的波形记录、震相拾取进行核对,分析过程中删去了不满足计算条件的地震记录,主要包括:①震相记录不清晰以及单台事件;②主震过后背景噪声的影响过大,导致台站波形记录不满足计算所需信噪比条件的地震事件。精选后,样本数量有一定变化(表1),其中2013年6月1区、2区、5区的样本数为0或1,样本数量太少,无法计算。
为满足本研究方法的基本原理并保证计算的合理性,选取震中周围不同方位上使用宽频带地震计的固定台站;台站与震群距离在70~150km,既保证台站与震群之间的距离远大于震群中地震之间的距离,又保证初至波为直达波。同时,由于所选地震震级较小,又要有尽量多的台站有清晰的记录,最终选取GZA(姑咱台)、EMS(峨眉山台)、YGD(仁寿台)、XJI(小金台)、YZD(油榨坪台)、JYA(井研台)、SMI(石棉台)、WCH(汶川台)、WME(沐川台)、JJS(中江台)10个台站(图1),且这10个台站均有清晰的记录。
将研究时段划分为2013年4月20-30日(第一时段)、5月1-31日(第二时段)、6月1-30日(第三时段)3个时段,分别求取每个时段内小震群的平均相关系数。
3 计算及结果
基于校核震相后的Pg,Sg到时,选取不同分量Pg和Sg波计算观测波形的傅里叶谱,并从速度谱转为位移谱。对每个台站记录数据的5个分量分别做频谱图,如图2为小金台(XJI)记录的2013年4月20日13时17分地震事件的Pg波和Sg波5个分量的频谱图,频谱显示图为“两段式”,且有明显的“拐点”。用MatLab中的退火算法,计算出波谱曲线的最佳拟合,求得每次地震每个台站的零频谱振幅值。
用计算所得零频谱振幅值,根据式(6)计算其线性相关系数,可以得到2次事件的相似性:式中:xij为一次事件在i台站的j谱值分量的对数;yij为另一次事件的谱值分量的对数;x、y分别是xij、yij的平均值。这里定义rxy为波形相关系数。如果该值接近1.0,那么各台记录到的2次事件波形应该相似,震源机制解的几何特征相同;若该值较低,则说明震源机制解的几何特征具有不同程度的差异(崔子健等,2012)。反映在波形上就表现为,相关系数较高的2次事件,其波形互相关性也较好,反之则较差,如图3所示。图3a中2次地震事件的平均相关系数为0.34,远低于图3b中的0.95,从波形上看,图3b的波形互相关要优于图3a。
计算得到单位时段内余震的平均相关系数(表2),计算结果显示,2区震后第一时段的平均相关系数最高,达0.809,4区第三时段的平均相关系数最低,仅0.524;从第一时段到第三时段整个研究区的总平均相关系数由0.785变至0.575。其变化趋势如图4、5所示。图4显示在同一时间段内,2区的平均相关系数最高,向外围逐渐降低。芦山地震主震震中位于3区,并非平均相关系数下降最快的区域。图5显示在主震之后,随着时间的推移,每个子区的平均相关系数均逐渐减小。
4 讨论
平均相关系数的变化规律反映到震源机制一致性上来,则是在主震刚发生后,震源机制的一致性相对较好,这可能是区域应力的聚集作用。而主震后随着能量的逐渐释放,区域应力得以恢复,此时余震的震源机制一致性逐渐变差。
研究结果表明,芦山主震过后应力释放使得应力场对于破裂方向的约束逐渐减弱,以致序列的震源机制一致性变差,相关系数降低。震源机制和应力场的一致,显示了构造应力场控制作用较强,反之,则表明构造应力场控制作用减弱,地震将以离散发生的中小地震为主(赵英萍等,2004)。
陈颙(1978)指出,某一岩层或某一构造受到应力作用,产生前震时,构造基本结构没有变化;而主震后,基本结构发生了变化,因此余震机制就显得紊乱。本文认为某一效应在主震前后所发生的变化,可视作基本结构变化的一种量度,根据这个道理,就可判断主震是否已经过去。地震之后大部分区域的应力得到释放(董培育等,2013),因此主震和较大地震发生后小震机制有一定的发散(朱航等,2006;崔子健等,2012;泽仁志玛等,2010)。此外,孕震应力场的应力强度对孕震区内地震的破裂方向有明显的约束作用,对单纯的小震序列而言,孕震应力场的应力强度较低,故震源机制比较紊乱(朱航,何畅,2014)。
小地震是地下介质中瞬间发生的微小破裂,震源机制解表示了微破裂的空间几何参数和破裂错动的方向。小范围一群微破裂几何参数的一致意味着微裂隙的定向排列。震源机制一致性的变化趋势,可反映区域应力的变化,结合其他研究结果,可以为地震分析预报工作提供参考。5结论
本文通过体波谱振幅方法对芦山地震余震序列进行计算和分析后,并从震源机制一致性的变化中探讨芦山地区的区域应力变化情况,得出以下结论:体波谱振幅相关系数分析方法不需要计算每一次地震事件的震源参数,只需震群相对集中且有一定数量的台站较好包围在震群周围,适于分析一个震群震源机制一致性的变化情况。
平均相关系数的变化可以反应震源机制一致性的变化,前者越高则震源机制一致性越好,反之则越差。大震过后余震序列的平均相关系数存在较明显的变化趋势,2区震后第一时段的平均相关系数最高,达0.809,4区第三时段的平均相关系数最低,仅0.524;从第一时段到第三时段整个研究区的总平均相关系数由0.785变至0.575。主震发生后随着时间的推移,各子区内地震的平均相关系数均逐渐减小;同一时段内,2区内平均相关系数最高,随着与该区距离的增大而逐渐减小。
总体来说,大震过后较短时间内发生的余震序列,其平均相关系数较高。随着时间的推移,平均相关系数逐渐降低,反映出随着能量的释放,震源机制一致性逐渐变差。
参考文献:
陈颙.1978.用震源机制一致性作为描述地震活动性的新参数[J].地球物理学报,21(2):142-159.
程万正,阮祥,张永久,2006.川滇次级地块震源机制解类型与-致性参数[J].地震学报,28(6):561-573.
崔子健,李志雄,陈章立,等.2012.判别小震群序列类型的新方法研究—谱振幅相关分析法[J].地球物理学报,55(5):1718-1724.
董培育,程惠红,曾祥方,等.2013.四川芦山MS7.0级地震导致周边断层的应力变化[J].科技导报,31(12):19-22.
付虹,王绍晋,李丽,等.2011.滇中地区震源机制一致性参数时空分布与强震活动[J].地震研究,34(2):113-118
国家地震局监测预防司.1997.测震学分析预报方法[M].北京:地震出版社,131-136.
刘泽民,刘东旺,夏仕安,等.2010.体波谱振幅相关系数法在肥东地震序列震后判定中的应用[J].地震地磁观测与研究,31(5):13-16.
泽仁志玛,刁桂苓,李志雄,等.2009.千岛岛弧2006年MW8.3地震前震源机制解的一致性变化[J].地震学报,31(4):167-170
泽仁志瑪,刁桂苓,李志雄,等.2010.大震前显示的地震震源机制趋于一致的变化[J],地震,30(1):108-114
赵英萍,刁桂苓,高景春,等,2004.张北强余震前震源机制解的一致性特征[J].华北地震科学,22(1):1-4.
朱航,何畅.2014.注水诱发地震序列的震源机制变化特征:以四川长宁序列为例[J].地球科学:中国地质大学学报,39(12):1776-1782.
朱航,刘杰,陈夫长.2006.采用体波谱振幅相关系数方法研究地震序列的震源机制变化过程[J].地震,26(2):1-11.
Lund B,Boovarson B.2002.Correlation of Microearthquake Body-WaveSpectral Amplitudes[J].Bull Seism Soc Amer,92(6):2419-2433.



摘要:利用体波谱振幅相关系数分析方法,对2013年4月20日至6月30日芦山MS7.0地震余震序列中四川地震台网固定台站记录的ML2.0~4.0地震的震源机制一致性进行了研究。将主要研究区分为5个子区,分区计算震群的平均相关系数。结果显示,同一时段内,震后2区平均相关系数最高,达0.809,随着与该区距离的增大而逐渐减小。4区2013年6月平均相关系数最低,仅为0.524;整个研究区的总平均相关系数由0.785变至0.575。主震发生后,随着时间的推移,各子区内地震的平均相关系数均逐渐减小;随着区域应力场能量的释放,震群的震源机制一致性逐渐变差。
关键词:芦山MS7.0地震;余震序列;谱振幅相关系数;震源机制一致性
中图分类号:P315.7 文献标识码:A 文章编号:1000-0666(2018)02-0251-07
0 引言
震源机制解描述了震源的几何特性,反映了地震破裂的运动学特征,是研究区域构造应力的基础。地震学的发展和数字记录的应用使震源机制的研究进入了新的阶段,目前有多种测定震源机制解的方法,如P波初动法、地震矩张量反演等。其中大多数方法对地震观测台站的记录数有较高的要求,目前由于受台网布局和观测点密度的制约,大量中小地震、尤其是小地震的台站记录数往往很有限,很难用P波初动等方法求出可靠的震源机制解,因此,直接求解小震震群中单个地震的震源机制解存在较大的困难。
对较大地震的前震与余震的波形进行研究,得到地震前后震源机制的变化过程,历来是地震预测研究关注的问题(刘泽民等,2010;付虹等,2011;泽仁志玛等,2009)。筹В?978)根据海城前震序列的研究,提出用震源机制的一致性作为判别前震的新参数;崔子健等(2012)认为谱振幅相关分析法可能是判定小震群类型的物理意义较为明确的方法,且具有实用价值;程万正等(2006)对川滇地区4个次级地块上的925次地震进行震源机制解一致性分析,通过对次级地块大量区域小震震源机制解的测定,给出了应力场变化信息。前震序列、余震序列‘震源机制的变化过程存在规律性,具有重要的地震前兆意义(国家地震局监测预防司,1997)。因此,对中小地震震源机制解进行综合分析,就有可能捕捉到与强震发生有关的应力场变化信息。朱航等(2006)曾提出了一种方法,即采用体彼谱振幅相关系数来研究地震序列中震源机制是否相似,该方法给出的不是单个地震的震源机制解,而是地震序列震源机制一致性的变化特征。
2013年4月20日8时2分,四川芦山发生MS7.0强震,根据中国地震台网中心测定,震中位置为(30.3°N,103.0°E),震源深度17km。主震后随着余震的发生,地壳内部能量得以释放,区域应力场也随之发生一些变化,本文利用体波谱振幅相关方法分析芦山MS7.0地震余震相关系数的变化规律,从震源机制一致性的变化中探讨芦山地区的区域应力变化情况。
1 基本原理及计算方法
在地震学中,台站j记录第i个地震波位移的谱振幅可表示为:
Ouj(f)=Mi(f)·Rij(θ,φ)·Pij(r)·Fij(f,r)·Gj(f)·Ij(f)(1)式中:f表示频率;r表示地震与台站之间的距离;Mi(f)是震源谱;Rij(θ,φ)為辐射图型因子;θ、φ表示地震到台站的方位角和离源角;Pij(r)是几何扩展系数,仅与距离相关;Fij(f,r)是地震波的衰减项;Ij(f)是仪器响应,Gj(f)是场地响应。其中,Mi(f)的表达式为:式中:M0为地震矩,fc为拐角频率。
如果2次地震(a,b)震源位置相同,或者2次地震震源之间的距离远小于地震到台站之间的距离,那么这2个地震到同一个台站的几何扩散、非弹性衰减、仪器响应和场地响应是一样的。对于同一频率,在同一个台站上2次地震事件的观测谱值之比可表示为:当f≤fc时,式(3)可表达为:式中:Oaj(f0)和Obj(f0)表示2个台站观测谱的零频谱值;
由式(4)可知,对于发生在同一震源区的2个地震,在同一个台站的零频观测谱值之比与其辐射图型因子之比线性相关,而辐射图型因子取决于震源机制解的几何特性(走向、倾角和滑动角)。可以推知,对同一震源区的不同地震在不同台站得到的零频观测谱值进行比较,应该可以得到不同地震之间的震源机制差异。
Lund和Boovarson(2002)提出一种计算体波谱振幅相关性的方法,即对同一震源区2次事件在相同台站的波形记录,使用直达P、S波的零频谱振幅值计算相关系数。
对于3分向地震波形记录,经过旋转每个台站可以得到5个零频谱值:垂向和径向P波(PZ和PR),垂向、径向和切向S波(SZ、SR和ST),称这5个谱值为谱值分量。根据台站和震中位置,计算台站在震源球上的方位角。然后根据地震与台站间的方位角,对台站记录的2个水平分量进行旋转,得到径向和切向分量:
R(t)=N(t)cos(Az)+EN、sin(Az) (5)
T(t)=-N(t)sin(Az)+E(t)cos(Az)式中:R(t)和T(t)表示径向和切向分量;N(t)和E(t)表示南北和东西分量记录;Az表示方位角。
2 资料选取及初步分析
2013年4月20日芦山MS7.0地震后,发生了大量余震,截至2013年6月30日,四川地震台网共记录到余震近万次。本文选取2013年4月20日至6月30日震中空间分布相对集中的1129次ML2.0~4.0地震序列做为研究对象。
由于研究区(30.1°~30.4°N,102.8°~103.1°E)范围较大,故将主要研究区划分为5个子区分别进行计算(图1),分别是1区(30.1°~30.2°N,102.8°~102.9°E)、2区(30.2°~30.3°N,102.8°~102.9°E)、3区(30.2°~30.3°N,102.9°~103.0°E)、4区(30.3°~30.4°N,102.9°~103.0°E)、5区(30.3°~30.4°N,103.0°~103.1°E)。这样,每个子区控制在经纬度0.1°左右的范围内(约11km×11km),分区后,每个子区内小震群相对于所选台站来看,可理想地看作是一个点。芦山地震主震震中位于3区内。
对所选余震的波形记录、震相拾取进行核对,分析过程中删去了不满足计算条件的地震记录,主要包括:①震相记录不清晰以及单台事件;②主震过后背景噪声的影响过大,导致台站波形记录不满足计算所需信噪比条件的地震事件。精选后,样本数量有一定变化(表1),其中2013年6月1区、2区、5区的样本数为0或1,样本数量太少,无法计算。
为满足本研究方法的基本原理并保证计算的合理性,选取震中周围不同方位上使用宽频带地震计的固定台站;台站与震群距离在70~150km,既保证台站与震群之间的距离远大于震群中地震之间的距离,又保证初至波为直达波。同时,由于所选地震震级较小,又要有尽量多的台站有清晰的记录,最终选取GZA(姑咱台)、EMS(峨眉山台)、YGD(仁寿台)、XJI(小金台)、YZD(油榨坪台)、JYA(井研台)、SMI(石棉台)、WCH(汶川台)、WME(沐川台)、JJS(中江台)10个台站(图1),且这10个台站均有清晰的记录。
将研究时段划分为2013年4月20-30日(第一时段)、5月1-31日(第二时段)、6月1-30日(第三时段)3个时段,分别求取每个时段内小震群的平均相关系数。
3 计算及结果
基于校核震相后的Pg,Sg到时,选取不同分量Pg和Sg波计算观测波形的傅里叶谱,并从速度谱转为位移谱。对每个台站记录数据的5个分量分别做频谱图,如图2为小金台(XJI)记录的2013年4月20日13时17分地震事件的Pg波和Sg波5个分量的频谱图,频谱显示图为“两段式”,且有明显的“拐点”。用MatLab中的退火算法,计算出波谱曲线的最佳拟合,求得每次地震每个台站的零频谱振幅值。
用计算所得零频谱振幅值,根据式(6)计算其线性相关系数,可以得到2次事件的相似性:式中:xij为一次事件在i台站的j谱值分量的对数;yij为另一次事件的谱值分量的对数;x、y分别是xij、yij的平均值。这里定义rxy为波形相关系数。如果该值接近1.0,那么各台记录到的2次事件波形应该相似,震源机制解的几何特征相同;若该值较低,则说明震源机制解的几何特征具有不同程度的差异(崔子健等,2012)。反映在波形上就表现为,相关系数较高的2次事件,其波形互相关性也较好,反之则较差,如图3所示。图3a中2次地震事件的平均相关系数为0.34,远低于图3b中的0.95,从波形上看,图3b的波形互相关要优于图3a。
计算得到单位时段内余震的平均相关系数(表2),计算结果显示,2区震后第一时段的平均相关系数最高,达0.809,4区第三时段的平均相关系数最低,仅0.524;从第一时段到第三时段整个研究区的总平均相关系数由0.785变至0.575。其变化趋势如图4、5所示。图4显示在同一时间段内,2区的平均相关系数最高,向外围逐渐降低。芦山地震主震震中位于3区,并非平均相关系数下降最快的区域。图5显示在主震之后,随着时间的推移,每个子区的平均相关系数均逐渐减小。
4 讨论
平均相关系数的变化规律反映到震源机制一致性上来,则是在主震刚发生后,震源机制的一致性相对较好,这可能是区域应力的聚集作用。而主震后随着能量的逐渐释放,区域应力得以恢复,此时余震的震源机制一致性逐渐变差。
研究结果表明,芦山主震过后应力释放使得应力场对于破裂方向的约束逐渐减弱,以致序列的震源机制一致性变差,相关系数降低。震源机制和应力场的一致,显示了构造应力场控制作用较强,反之,则表明构造应力场控制作用减弱,地震将以离散发生的中小地震为主(赵英萍等,2004)。
陈颙(1978)指出,某一岩层或某一构造受到应力作用,产生前震时,构造基本结构没有变化;而主震后,基本结构发生了变化,因此余震机制就显得紊乱。本文认为某一效应在主震前后所发生的变化,可视作基本结构变化的一种量度,根据这个道理,就可判断主震是否已经过去。地震之后大部分区域的应力得到释放(董培育等,2013),因此主震和较大地震发生后小震机制有一定的发散(朱航等,2006;崔子健等,2012;泽仁志玛等,2010)。此外,孕震应力场的应力强度对孕震区内地震的破裂方向有明显的约束作用,对单纯的小震序列而言,孕震应力场的应力强度较低,故震源机制比较紊乱(朱航,何畅,2014)。
小地震是地下介质中瞬间发生的微小破裂,震源机制解表示了微破裂的空间几何参数和破裂错动的方向。小范围一群微破裂几何参数的一致意味着微裂隙的定向排列。震源机制一致性的变化趋势,可反映区域应力的变化,结合其他研究结果,可以为地震分析预报工作提供参考。5结论
本文通过体波谱振幅方法对芦山地震余震序列进行计算和分析后,并从震源机制一致性的变化中探讨芦山地区的区域应力变化情况,得出以下结论:体波谱振幅相关系数分析方法不需要计算每一次地震事件的震源参数,只需震群相对集中且有一定数量的台站较好包围在震群周围,适于分析一个震群震源机制一致性的变化情况。
平均相关系数的变化可以反应震源机制一致性的变化,前者越高则震源机制一致性越好,反之则越差。大震过后余震序列的平均相关系数存在较明显的变化趋势,2区震后第一时段的平均相关系数最高,达0.809,4区第三时段的平均相关系数最低,仅0.524;从第一时段到第三时段整个研究区的总平均相关系数由0.785变至0.575。主震发生后随着时间的推移,各子区内地震的平均相关系数均逐渐减小;同一时段内,2区内平均相关系数最高,随着与该区距离的增大而逐渐减小。
总体来说,大震过后较短时间内发生的余震序列,其平均相关系数较高。随着时间的推移,平均相关系数逐渐降低,反映出随着能量的释放,震源机制一致性逐渐变差。
参考文献:
陈颙.1978.用震源机制一致性作为描述地震活动性的新参数[J].地球物理学报,21(2):142-159.
程万正,阮祥,张永久,2006.川滇次级地块震源机制解类型与-致性参数[J].地震学报,28(6):561-573.
崔子健,李志雄,陈章立,等.2012.判别小震群序列类型的新方法研究—谱振幅相关分析法[J].地球物理学报,55(5):1718-1724.
董培育,程惠红,曾祥方,等.2013.四川芦山MS7.0级地震导致周边断层的应力变化[J].科技导报,31(12):19-22.
付虹,王绍晋,李丽,等.2011.滇中地区震源机制一致性参数时空分布与强震活动[J].地震研究,34(2):113-118
国家地震局监测预防司.1997.测震学分析预报方法[M].北京:地震出版社,131-136.
刘泽民,刘东旺,夏仕安,等.2010.体波谱振幅相关系数法在肥东地震序列震后判定中的应用[J].地震地磁观测与研究,31(5):13-16.
泽仁志玛,刁桂苓,李志雄,等.2009.千岛岛弧2006年MW8.3地震前震源机制解的一致性变化[J].地震学报,31(4):167-170
泽仁志瑪,刁桂苓,李志雄,等.2010.大震前显示的地震震源机制趋于一致的变化[J],地震,30(1):108-114
赵英萍,刁桂苓,高景春,等,2004.张北强余震前震源机制解的一致性特征[J].华北地震科学,22(1):1-4.
朱航,何畅.2014.注水诱发地震序列的震源机制变化特征:以四川长宁序列为例[J].地球科学:中国地质大学学报,39(12):1776-1782.
朱航,刘杰,陈夫长.2006.采用体波谱振幅相关系数方法研究地震序列的震源机制变化过程[J].地震,26(2):1-11.
Lund B,Boovarson B.2002.Correlation of Microearthquake Body-WaveSpectral Amplitudes[J].Bull Seism Soc Amer,92(6):2419-2433.

