《河南省居民消费价格指数预测》-经济学论文，经济论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

河南省居民消费价格指数预测

范文

李海洋

摘要：为提高CPI建模精度，本文使用SARIMA、SARIMA-LSTM、LSTM三个模型对河南省月度CPI进行建模预测。研究发现SARIMA-LSTM模型效果最优，可以反映河南省居民消费价格指数的真实状况，用于CPI实际预测。

关键词：SARIMA;SARIMA-LSTM;LSTM

中图分类号：F23文献标识码：Adoi：10.19311/j.cnki.16723198.2020.25.047

对于CPI，建立合适的模型，提高其预测精度，对政府制定宏观经济政策具有极大现实意义。现在，对于CPI预测，不同学者进行了许多研究。研究方法主要分为两种：

（1）单一模型法，如ARIMA、SARIMA、灰色模型法等。袁志强、陈锐使用ARIMA模型利用R软件对国内CPI进行了短期预测，倪颖、年靖宇对重庆市CPI进行了预测;张甜瑞对陕西省CPI建立了SARIMA模型;李志超、刘升对上海市CPI建模，发现ARIMA和灰色模型效果相当，回归模型较差。

（2）组合模型法，如ARIMA-SVM、ARIMA-BP等。梁晓莹基于ARIMA和SVM根据整体误差最小化原则对郑州市CPI进行组合预测，比单一模型效果好。吴晓峰、杨颖梅和陈垚彤利用BP拟合ARIMA残差，整体效果较优。

深度学习中长短期记忆网络（LSTM），对于非线性数据拟合较好，并且在金融、医学、水文等时间序列预测领域已取得不少进展。欧阳红兵、黄亢和闫洪举使用LSTM对道琼斯工业指数日收盘价进行预测，发现LSTM能捕获序列的短期和长期态势，效果较优。李琳等将LSTM用于新疆地区慢性阻塞性肺病的月门诊量进行预测，并与ARIMA比较，发现LSTM精度较高。胡庆芳等将LSTM用于汉江上游安康站日径流预测，发现多因素条件下效果较好。

综上所述，关于CPI预测并未有统一的方法。并且，较少有学者结合SARIMA对线性拟合和LSTM对非线性拟合的优势对CPI进行建模预测。本文以河南省月度同比CPI为研究对象，尝试使用SARIMA-LSTM对其建模，以探究其在CPI预测中的效果。

1模型简介

1.1SARIMA模型

对于随机时间序列yt，季节性移动平均差分自回归SARIMA（p，d，q）（P，D，Q）s，公式如下：

ΦpLAPLs（ΔdΔDsyt）=ΘqLBQLsvt（1）

其中，Δd表示非季节性差分算子，Δd=1-Ld;ΔDs表示季节性差分算子，ΔDs=1-LDs;Φp（L）为非季节性自回归算子，Φp（L）=1-φ1L-φ2L2-…-φpLp;APLs为季节性自回归算子，APLs=1-α1Ls-α2L2s-…-αPLPs;ΘqL为非季节性移动平均算子，ΘqL=1+θ1L+θ2L2+…+θqLq;BQLs为季节性移动平均算子，BQLs=1+β1Ls+β2L2s+…+βQLQs;vt为白噪声。

1.2LSTM

长短期记忆神经网络（LSTM），解决了计算过程中梯度消失的问题。对于输入xt，LSTM隐层输出表示为ht，具体计算过程如下：

it=σWiht-1，xt+bi（2）

ft=σWfht-1，xt+bf（3）

c～t=tanhWcht-1，xt+bc（4）

ct=ft⊙ct-1+it⊙ct（5）

ot=σWoht-1，xt+bo（6）

ht=ot⊙tanhct（7）

其中，W为权重矩阵，b为偏移列向量。LSTM将信息存放在门控单元中，f是遗忘门，表示对于当前时刻的输入xt，决定了从上一时刻传来的信息要丢弃的部分。i表示输入门，决定在t时刻应该更新哪些值，c～是一个候选值的向量，将i和c～组合起来得到c对神经元状态进行更新。o是输出层，决定神经元状态需要输出的部分。h是网络的输出。

2实证分析

2.1数据来源

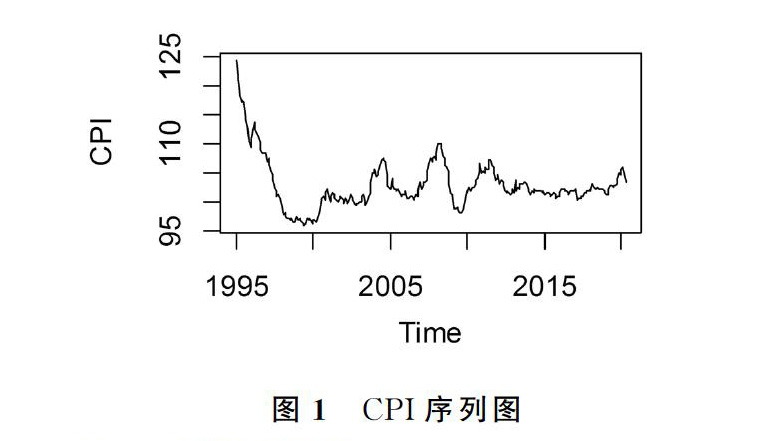
本研究以河南省为研究对象，选取其1995年1月-2020年4月月度同比CPI数据进行分析，数据来源于瑞思数据库。CPI走势如图1，从中可以看出，2004年、2008年CPI较高，2012年之后较为平稳。近来，受猪肉价格影响，CPI较高。

2.2SARIMA模型构建

（1）平稳性检验。使用R软件中adf.test函数进行单位根检验，结果如下：

Augmented Dickey-Fuller Test

data：CPI

Dickey-Fuller = -4.164， Lag order = 6， p-value = 0.01

alternative hypothesis： stationary

p值为0.01，在5%的显著性水平下拒绝原假设“序列不平稳”，由此可知，数据平稳。

（2）模型识别。加载R语言forecast包，使用函數auto.arima根据AICc最小准则对1995年1月-2020年4月CPI进行模型构建，模型为SARIMA（2，0，1）（1，0，0）12，系数估计见表1。其中，残差方差估计值为0.4822，对数似然估计值为-322.05，赤池信息准则AIC为656.11，AICc为656.39，贝叶斯信息准则BIC为678.41。

使用confint函数对模型系数进行检验，结果见表2。由表2可知，在95%的置信区间下，参数取值范围均不含0，即系数显著。

（3）模型诊断。使用Box.test函数对残差进行检验，得

X-squared = 7.6586， df = 6， p-value = 0.2642

从Box检验得知残差符合正态性假设且不相关，认为模型拟合比较充分。

对2019年11月-2020年4月CPI进行预测，结果见表3。其均方根误差为0.8227，建模精度较高，基本可以描述2019年11月到2020年4月CPI月度同比数据。

2.3SARIMA-LSTM模型构建

针对SARIMA模型对非线性数据拟合不好的问题，本文使用LSTM对其残差进行建模。使用1995年1月-2019年10月的残差进行训练模型，对2019年11月-2020年4月的残差进行测试。经对比，数据平滑期设置为8，隐藏层节点数为100，训练次数为150。测试集的均方根误差为0.6316，相比SARIMA模型减少了23%。残差预测值加上SARIMA模型预测值即为SARIMA-LSTM预测值，结果见表3。

2.4LSTM模型构建

本文同时使用LSTM模型对1995年1月-2019年10月CPI数据直接建模，并对2019年11月-2020年4月数据预测，预测均方根误差为1.0651，比SARIMA、SARIMA-LSTM均要高。CPI预测值见表3。

3结语

本文利用模型SARIMA、SARIMA-LSTM、LSTM对河南省1995年1月-2020年4月月度同比CPI进行对比建模，SARIMA-LSTM建模精度最高，SARIMA次之，LSTM效果最差。由此可知，模型SARIMA-LSTM可以较好地对河南省CPI进行建模，以预测河南省CPI的状况。对于本文数据，LSTM效果较差，其它数据中LSTM效果可能更优，针对不同数据，需做具体分析。下一步研究可以使用更多因素利用LSTM对CPI进行对比建模，以提高预测准确度。

参考文献

[1]袁志强，陈锐.基于ARMA模型的CPI短期预测研究[J].中国集体经济，2018，（03）：6465.

[2]倪颖，年靖宇.基于ARIMA模型的居民消费价格指数走势实证分析与预测——以重庆市为例[J].贵州商学院学报，2018，（02）：1423.

[3]张甜瑞.陕西省居民消费价格指数预测[J].合作经济与科技，2020，（07）：6769.

[4]李志超，刘升.基于ARIMA模型、灰色模型和回归模型的预测比较[J].统计与决策，2019，（23）：3841.

[5]梁晓莹.基于ARIMA-SVM模型的郑州市CPI预测研究[J].洛阳理工学院学报（社会科学版），2019，（04）：2631.

[6]吴晓峰，杨颖梅，陈垚彤，等.基于BP神经网络误差校正的ARIMA组合预测模型[J].统计与决策，2019，（15）：6568.

[7]欧阳红兵，黄亢，闫洪举，等.基于LSTM神经网络的金融时间序列预测[J].中国管理科学，2020，（04）：2735.

[8]李琳，王哲，张学良，等.基于LSTM深度神经网络的月门诊量预测精度研究[J].中国数字医学，2019，（01）：1417.

[9]胡庆芳，曹士圯，杨辉斌，等.汉江流域安康站日径流预测的LSTM模型初步研究[J].地理科学進展，2020，（04）：636642.

[10]HOCHREITER S，SCHMIDHUBER J.Long short-term memory[J].Neural Computation，1997，（8）：17351780.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。