《基于时间序列的股票价格走势分析》-管理学论文，营销论文-论文范文参考-科学狗论文网

标题

基于时间序列的股票价格走势分析

范文

摘要：随着当代经济的不断发展，金融市场已经成为经济发展的重要部分，而股票市场作为金融市场的重要组成部分，便与国民经济密切相关。对于投资者而言，如何及时了解价格波动从而准确分析股票市场行情，是决策过程中的一个关键问题;对于股票市场的管理者来说，如何把握股市动态，从而营造稳定健康的交易环境，也是一项非常艰巨的任务。因此，更好地了解股市的波动特征，以及从中探索某些规律，对我们学习金融理论和进行金融实践都具有重要的意义。本文以2009-2018年的沪深300指数为例，对ARIMA模型、ARCH模型和AR-GARCH模型进行拟合，比较其在股票价格走势上的优劣，再用通过检验的拟合模型对股价进行一个短期的预测。最后发现AR-GARCH模型对原序列有较好的拟合效果，并且获得了较为精确的预测结果。

关键词：时间序;ARIMA模型;ARCH模型;AR-GARCH模型

1.数据预处理

1.1? 平稳性检验

本文选取了2009年1月至2018年12月的沪深300指数每个工作日的收盘价作为研究对象，绘制其时序图并作出初步分析。

由原序列时序图可以看出，该序列有不太明显的周期性，直接观察无法确定其是否平稳，此时我们可以借助自相关图进一步判断序列是否平稳。

根据原序列的ACF图可以看出，随着延迟期数k的增加，ACF一直在零轴上方为正，而且衰减到零的速度非常慢，因此可以判断原序列为非平稳序列。

1.2? 纯随机性检验

此时，再检验序列的纯随机性。结果显示，在各阶延迟下LB检验统计量的P值都远远小于0.05，因此可以确定原序列属于非白噪声序列，有继续研究下去及对未来预测的意义。

2.股票价格建模

2.1? ARIMA模型

差分运算有着非常强大的确定性信息提取功能。通常来说，具有随机性趋势的非平稳时间序列会在适当的差分之后显示出平稳序列的性质，此时我们称这个非平稳序列为差分平稳序列。对于这种差分平稳序列我们就需要利用ARIMA模型来进行拟合。

一阶差分后的时序图显示，序列一直围绕零轴波动，没有明显的规律，此时用单位根检验得p值<0.05，所以拒绝原假设，可以认为序列平稳。然后，再对一阶差分后的序列进行白噪声检验，得到在各阶延迟下LB检验统计量的P值都<0.05，因此得出一阶差分后的序列是平稳非白噪声序列，可以使用ARIMA模型对其进行拟合。

可以认为自相关系数和偏自相关系数均显现出了拖尾性，无法准确定阶。此时利用R軟件提供的auto.arima函数自动识别模型阶数，最终确定对原序列拟合ARIMA（3，1，2）模型。

这时对模型进行显著性检验来检验模型的有效性。由于各阶延迟下LB统计量的P值都大于0.05，因此可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型是显著有效的。

根据输出的拟合结果，得到拟合模型为：

2.2? ARCH模型

当使用ARIMA模型拟合非平稳序列时，通常直接默认[εt]为零均值白噪声序列。但在此之前，直接忽视了对方差齐性的任何检验，就直接默认了残差序列肯定满足这样一个条件。在处理金融时间数据时，忽视异方差的存在会严重低估残差的方差，使得参数的显著性检验失去意义，进而使模型的拟合精度受到影响。

在实际处理金融数据时，广泛采用的还是自回归条件异方差模型，简称ARCH模型。

具有

结构的模型称为q阶自回归条件异方差模型，简记为ARCH（q）。

考察原时间序列的方差齐性，经过平方处理后的残差序列明显地呈现出异方差的特征，这时需要对它做进一步的处理。由于异方差函数的具体形式未知，因此拟合条件异方差模型。

接下来对残差序列进行ARCH检验。通常使用Portmanteau Q检验和LM检验这两种检验统计方法。检验后发现，在各阶延迟下，Portmanteau Q检验统计量和LM检验统计量的P值均<0.05，所以拒绝原假设，认为该序列方差非齐且具有自相关关系，可以使用ARCH模型来提取残差平方序列中蕴含的相关信息。

得到拟合模型是ARCH（3）模型：

ARCH模型拟合的95%置信区间的范围，因为考虑了一阶差分后序列的波动特征，所以ARCH模型更好地拟合了一阶差分后序列的集群效应波动特征。

2.3 AR-GARCH模型

由于残差序列[et]在先前的检验中已被发现具有自相关性，所以需要先对它进行自回归模型的拟合。

在条件异方差检验下，各阶延迟下Portmanteau Q检验统计量均小于0.05显著性水平，说明ARIMA（3，1，2）存在异方差，于是对它拟合GARCH（1，1）模型，并根据该模型的拟合结果绘制波动的95%置信区间图。

综合水平模型和波动模型，最终得到完整的AR-GARCH拟合模型为：

图2-2给出了AR-GARCH模型拟合的残差序列波动置信区间，

进行比较后，发现AR-GARCH模型拟合结果绘制的95%置信区间比ARCH模型拟合的95%置信区间更加贴合原序列的真实波动情况，说明AR-GARCH模型的拟合效果更好，对序列波动的预测也将更加准确。

2.4? 模型比较

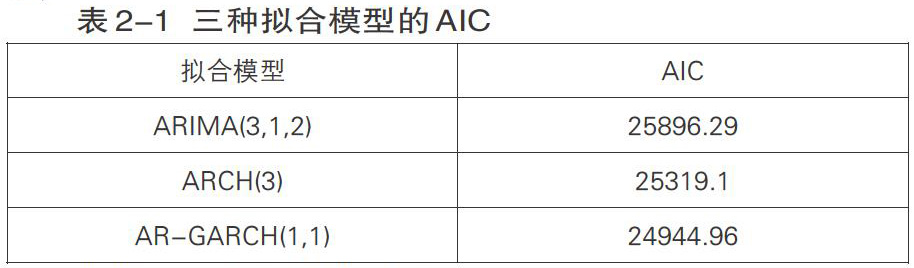
本章对沪深300股票价格进行了ARIMA（3，1，2）、ARCH（3）和AR-GARCH（1，1）三种模型的拟合，三种模型都通过了显著性检验，且都获得了不错的拟合效果。为了得到一个相对最优的拟合模型，需要运用最小信息量准则（AIC）来对这三个模型进行比较。我们运用如下公式来计算拟合模型的AIC的值：

AIC=-2ln（模型的极大似然函数值）+2（模型中未知参数个数）

根据AIC最小原则，比较得出AR-GARCH（1，1）是相对最优模型，ARCH（3）次之，ARIMA（3，1，2）再次之。

3.模型预测

3.1? AR-GARCH模型预测

选取相对最优模型，利用“rugarch”程序包用拟合好的AR-GARCH模型做预测，并将残差序列的预测值转化为原序列的预测值

由于此时已经得到了沪深300指数未来10天收盘价的真实值，于是可以通过比较真实值与预测值的误差来判断模型预测的优劣。接下来将三种模型获得的预测值与真实值进行比较：

其中，ARIMA（3，1，2）模型与ARCH（3）模型预测值的相对误差非常接近，可以认为这两种模型的预测效果差不多。而GARCH（1，1）模型的相对误差明显小于前两个模型，可以认为GARCH（1，1）模型的预测精度是最高的，即预测结果会更接近真实值。这个结果也与上一章比较模型优劣的结果一致。

3.2 横向预测

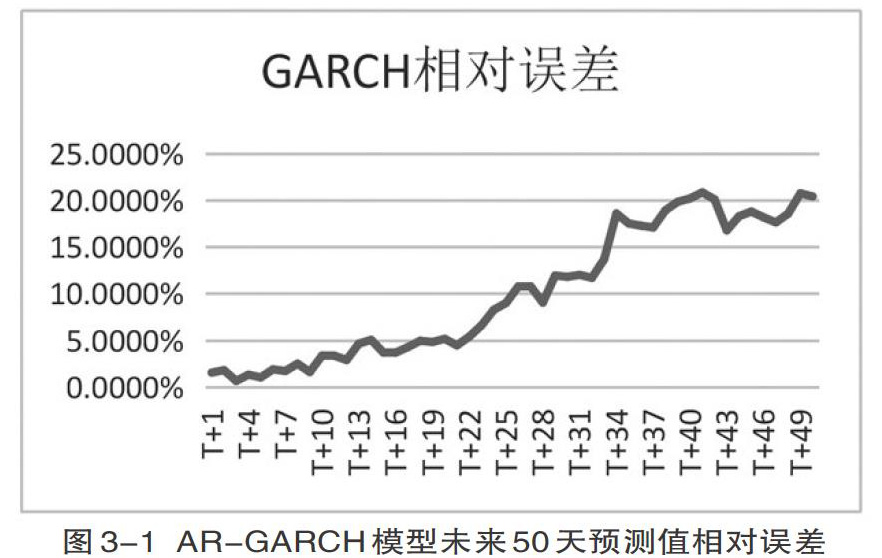
为了检验模型的长期预测效果，这里选用上述模型中预测效果最好的AR-GARCH（1，1）模型来对未来50天（约为2019年1-2月份）的收盘价进行预测。

由图3-1可以很明显地看出，随着期数的增加，AR-GARCH（1，1）模型的预测值与实际值的相对误差逐渐增大，到第50期时，相对误差已经超过了20%，也就是说该模型的预测精度越来越低，已经失去了准确预测收盘价的能力。

4.结论

本文主要讨论了求和自回归移动平均模型和条件异方差模型在股票价格时间序列分析中的应用。通过对沪深300股价进行三种模型的拟合，都成功建立了显著性模型，再一次证明了股票价格的可预测性：

（1）在本文研究的案例中，残差序列的异方差函数是具有长期自相关性的，因此在使用ARCH模型進行拟合时会产生高阶移动平均，而用GARCH模型拟合时就可以克服这一问题，提高拟合精度。所以对于股票价格时间序列这类异方差函数长期自相关的序列，选择使用GARCH模型拟合可以获得相对最优的拟合效果，从而得到更准确的预测。

（2）短期预测的结果与实际值相差并不大，预测的相对误差基本可以控制在2%以内，说明拟合的效果非常好，可以利用该模型对近期股市进行短期预测，帮助投资者做出更好的投资决断。但是在使用该模型进行长期预测时，结果不尽如人意，预测精度明显下降，失去准确预测的能力。

（3）时间序列作为金融市场分析的有效工具，有着巨大的实用价值和发展前景。通过时间序列来探寻股票价格波动的规律，对投资者进行投资决策、规避风险、获得最大收益有重要的参考意义。然而对股票市场规律的研究是十分复杂的，本文仅通过历史数据对沪深300的走势进行了一些分析和预测，并未考虑股票的投资收益率、风险溢价等指标，如何处理原始数据并选择最优模型还需要进一步的研究来完善。

作者简介：

黄旻浩（1996-? ），男，汉族，江苏省无锡市人，香港中文大学理学硕士研究生在读，统计机器学习。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。