《基于GARCH模型的比亚迪收益率研究》-管理学论文，营销论文-论文范文参考-科学狗论文网

标题

基于GARCH模型的比亚迪收益率研究

范文

摘要：在世界汽车行业由传统汽车向新能源汽车转型的时代背景下，以比亚迪为代表的中国汽车类公司生产新能源汽车的业务发展前景受到投资者广泛关注。比亚迪汽车公司已在A股上市，而在A股市场中，股票价格频繁波动是其最明显的特征之一，科学、合理分析比亚迪股票收益率的波动变化情况对资产持有者如何选择具有重要意义。本文基于2015-2019年1220个日收盘价数据构建关于比亚迪股票日收益率的时间序列，结果显示出，受市场和政策条件影响，比亚迪公司的股票收益率波动变化起伏较大。由于主营业务推陈出新，市场不确定因素增加，2016年间收益率具有波动最大的特征;因市场对新业务反馈良好及国家补贴政策利好的影响，2017年间波动较小;受宏观车市略微下行影响及补贴政策收紧影响，2018年起收益率波动变大但随后基本保持不变。

关键词：比亚迪;收益率;GARCH模型

一、研究背景和意义

如今，由于全球面临能源消耗和环境污染严重的问题，世界汽车产业正由传统汽车向新能源汽车转型。在“新能源汽车”技术发展还未成熟的机遇期，以比亚迪为代表的新能源汽车公司正抓住该契机大力推动企业自身的创新发展。比亚迪公司的投资价值高低成为金融市场的热点问题，它的收益率变化受到社会各界投资者的广泛关注。

由于股票价格频繁剧烈的波动，股票价格的时间序列经常表现出一个时期的波动明显地大于另一时期的特征。自从Engle首次利用ARCH模型来刻画条件异方差随时间的变化以来，自回归条件异方差模型得到了广泛的应用及发展，尤其是在金融市场及金融衍生品等领域。在Bollerslev通过对ARCH模型进行多种改进，增加考虑了异方差函数的p阶段自相关性，有效拟合了具有长期记忆性的异方差函数，最终将其模型的干扰项的条件方差构成了一个ARMA过程，即称为 GARCH模型，它能准确描述时间序列的条件异方差性和波动聚集性。国外学者的研究结果表明，GARCH模型在预测金融资产收益率方差方面是比较成功的。

本文基于2015年-2019年的1220个日收盘价数据，计算得日收益率，再利用GARCH模型，刻画出随时间变化而变化的条件方差，科学合理地反映比亚迪公司的收益率即期波动的特征，并根据即期实际情况进行分析。以此，为公司外部利益相关者，了解公司发展的状况，并根据公司发展的状况，制定相应的投资决策提供一些参考。

二、方法介绍

为获得金融时间序列通常具有的波动集聚性，Engle （1982）首先提出了自回归条件异方差（ARCH）模型。但许多实证表明，为了更好地获得条件异方差性，应该选取高阶的ARCH模型，这将增加要估计的参数，从而降低参数估计的效率。针对这个问题1986年，Bollerslev在ARCH模型中增加了自回归项，对ARCH模型的条件方差函数进行拓展，这个模型被称为广义ARCH模型——GARCH。相对于ARCH，GARCH模型的优点在于：可以用较为简单的GARCH模型来代表一个高阶ARCH模型，使待估参数大为减少，从而使得模型的识别和估计都变得比较容易。故本文使用GARCH模型，其数学模型如下：

三、实证分析

1.平稳性检验

本文选取的GARCH模型需要建立在时间序列平稳且非白噪声序列的基础上。在Rstudio软件中对序列进行随机性检验后的结果显示，在各阶延迟下LB检验统计量的P值窦非常小（< 0.05），所以有很大的把握断定比亚迪股票日收益率属于非白噪声序列。随后采用自相关（ADF）图检验来确定其平稳性。ADF的检验结果图如图1所示：

可以看到样本自相关图显示延迟10阶后，自相关系数都落入2倍标准差范围之内，而且自相关系数向零衰减的速度比较快。由时序图和样本自相关图的性质可以认为该序列平稳。

2.提取水平信息并预测未来水平

为确定水平信息，还需进行偏自相关（PACF）检验。PADF的检验结果图如图2所示：

结合自相关图，可见自相关系数和偏自相关系数均显示出不截尾的性质，为了避免因个人经验不足而导致的模型识别不准确的问题，本文使用了R中提供的auto.arima函数。该函数基于信息量最小原则自动识别模型阶数，并给出了该模型的参数估计值。使用AIC准则作为信息量，得到的系统自动定阶结果为拟合ARMA （1，2）模型，得到该模型的口径为：

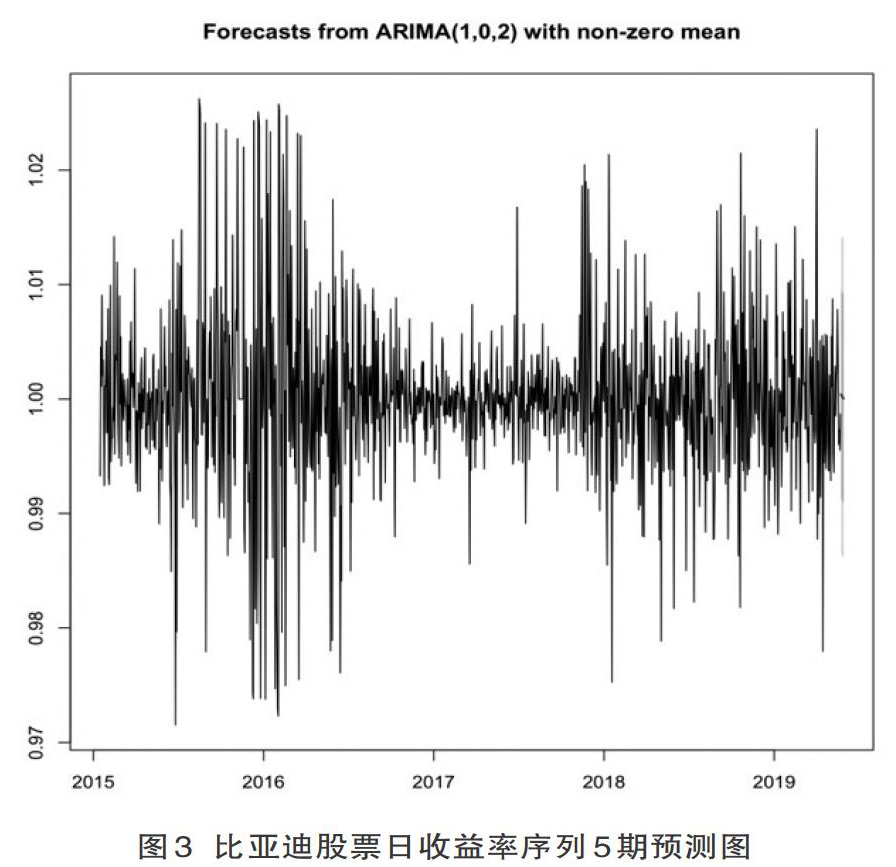
此时通过模型的显著性检验，即通过残差白噪声检验，模型有效。随后调用forecast函数完成从2019年6月17日后5个交易日的预测工作，预测图如图3所示：

3.条件异方差檢验（Portmanteau Q 检验）

1983年Mcleod和Li提出了Portmanteau Q统计方法，用于检验残差平方序列的自相关性。该检验方法的构造思想是：如果残差序列方差非齐性，且具有集群效应，那么残差平方序列通常具有自相关性。所以方差非齐检验可以转化为残差平方序列的自相关性检验。

Portmanteau Q检验的假设条件为：

H0：残差平方序列纯随机（方差齐性）

H1：残差平方序列自相关（方差齐性）

用[ρk]表示残差平方序列[ε2k]的延迟k阶自相关系数，则该假设条件可以等价表达为：

H0：[ρ1=ρ2=…ρq=0][?] H1：[ρ1，ρ2，…，ρq不全为零]

原假设成立时，Portmanteau Q统计量近似服从自由度为q -1的[χ2]分布

[Qq～χ2（q-1）]

当[q]检验统计量的P值小于显著性水平[α]时，拒绝原假设，认为该序列方差非齐且具有自相关关系。在R中进行Portmanteau Q检验后的结果显示残差序列显著方差非齐，且具有长期相关性。

4.拟合模型

在实际操作中，对GARCH模型中的p，q经常赋值为1，即GARCH（1，1）。

构造GARH（1，1）模型，得到完整拟合模型为：

[xt=600.6849+0.4338xt-1+εt-0.4829εt-1-0.0886εt-2+vt，]

[其中 vt～N0，116579]? ? [vt=htet ]? [ht=0.9015ht+0.09510vt-1]

可用来对短期内比亚迪公司的股票收益率进行预测。

四、结论和不足

通过以上实证分析，可以得到以下结论：受市场和政策条件影响，比亚迪公司的股票收益率波动变化起伏较大。具体而言，由于主营业务推陈出新，不确定因素增加，而短期市场对这类事件反应，导致了2016年间收益率具有波动最大的特征;因市场对新业务反馈良好及国家补贴政策利好，市场预期较好，2017年间波动较小;受宏观车市略微下行影响及补贴政策收紧影响，对整个车市的市场预期较差， 2018年起收益率波动变大，由于比亚迪公司主营业务盈利能力较强，波动率随后基本保持不变。

本文通过GARCH模型，对比亚迪公司的收益率进行了分析，验证了GARCH模型在实际经济环境下的应用可能。同时由于数据的不完备性，时间跨度的长度，市场的随机性，使用时间序列模型对经济市场进行分析预测具有一定参考价值而不尽准确。

作者简介：

刘颖琪（1998-? ），女，汉族，广东湛江遂溪县，苏州大学数学科学学院，统计专业。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。