《初中数学中考试题解题策略研究》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

初中数学中考试题解题策略研究

范文

宁丽曼

摘要：新时代考试理念之下，重视立足基础，不偏不难，体现数学探究活动过程，彰显对学生数学核心素养考查，有助于促进学生的数学思维能力。学生掌握到中考数学解题方式，数学成绩就会明显偏高。因此，初中数学教师必须要重视起学生数学解题能力的培养。该文将就中考数学的解题方法进行深入的分析和探究。

关键词：中考;数学试题;多角度思考

中图分类号：G4 ?文献标识码：A ?文章编号：（2020）-37-350

一、联系生活，让生活为中考服务

近些年，无论是全国统一卷还是地方卷的中考数学题目中有很多题目都与生活有着非常紧密的联系，这些联系生活的题目已经成为了当前中考数学编制题目的一种趋势。在解决问题的过程中，学生们随时可以感受到数学知识和生活之间的联系，学生们也会因为接触到这些题目而更加关注身边的生活，会关乎到社会中的一些热点问题等。因此，中考数学解题方法的第二大技巧，笔者将其总结为联系生活，让生活为中考服务。举例说明：在重庆2018中考数学试卷中，出现过這样一道题目：图1中的折线ABC表示某汽车的耗油量（单位：L/km）与速度x（单位：km/h）之间的函数关系（30≤x≤120），已知线段BC表示的函数关系中，该汽车的速度每增加Ikm/h，耗油量増加0.002L/km。（1）当速度分别为50km/h、100km/h时，该汽车的耗油量分别为？（2）求线段AB所表示的yx之间的函数表达式。（3）速度是多少时，该汽车的耗油量最低·最低是多少·

这到数学题目就将学生们在日常生活中经常会接触到的一个词“汽车耗油量”作为了问题情境，这种生活类的问题情境会带给学生们似曾相识的感觉，但是这种感觉却真的只是似曾相识，因为这道题目当中也会有所创新，其所包含的知识点多且细，虽然题目看似没有什么太大的变化，但是却做到了常考常新、不落俗套。

二、积极培养自己的思维能力

在中考数学的解题方法中，其非常需要学生们正确运用自己的思维能力，要多思考，敢思考，当一种解题方式行不通时，要尝试多去从另外的角度去思考和分析，要找准这些数学题目出现在中考试卷中的原因和目的，产生整体思维和意识，从宽到窄，从大到小去思考和分析具体的数学题目。举例说明：如图2所示，0是△ABC内一点，⊙0与BC相交于F，C两点，且与AB，AC分别相切于点D，E，DE∥BC连接DF，EC。

（1）求证：AB=AC。

（2）已知AB=10，BC=12，求四边形DFCE是矩形时⊙O的半径。

当看到这道数学题目时，学生们要下意识地认识到这道题目要考察的是图形与几何中的重点知识，分析这道题目中涉及到了哪些知识点，比如勾股定理、矩形的性质、三角形的相似等，要学会洞察这道数学题目出现在试卷中的本质和目的，建立起整体思维，进而确保回答问题的全面性和完整性，不要遗落任何一处细节问题。

三、注重多角度思考综合与实践题型

（一）试题呈现

以2018成都中考数学22题为例，在数学活动课上，老师出示了这样一个问题：如图3，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM.试判断线段AM与DE的位置关系.

试题分析：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：

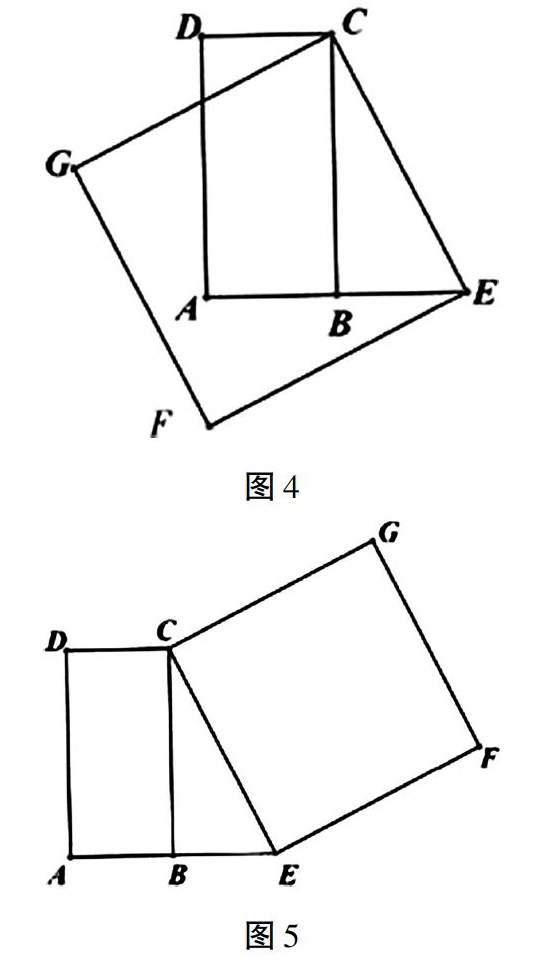
反思交流：上述证明过程中的“依据1”“依据2”分别是指什么·试判断图3中的点A是否在线段CF的垂直平分线上，请直接回答，不必证明。如图4连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明。

（二）探索发现

如图5，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C和点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明.

（三）试题思考

试题突出数学核心素养，关注探究实践活动经历，对数学教学具有很好的导向作用。探究活动的范例试题结构包括有“问题情境”探究展示”“反思交流”“探索发现”四部分，其以矩形为载体，构造直角角形、正方形等情境，围绕有关“点在线段的垂直平分线”问题展开探究活动.“问题情境”先是对特殊矩形进行图形延展，出现直角三角形和正方形，要求判断图中两线段的位置关系.“探究展示”环节为学生探究、讨论后出示的一种解答方案.“反思交流”首先体现良好的思维习惯，对上面某小组展示的解答过程寻找推理依据，并联想、提出“点A是否在线段CF的垂直平分线上”的相关问题，接着给出创新小组受如前探究活动“启发”的类比联想，重新构建直角三角形、正方形新情形。如图5，猜想、发现具有类似“点在线段垂直平分线上”的结论.“探索发现”，在前一环节的基础上又产生联想，对称性地変化所构正方形“CE为一边在CE的右上方作正方形”，类比性的正常思维提出，是否又存在“点在线段垂直平分线上的特征”猜测等.试题的几个环节具有一定的关联性.以“点在线段垂直平分线上”为主线，进行逻辑性的、环环相扣的类比，产生一系列的猜想，并给予推理论证，学生经历、体现如此过程的训练，有助于形成正确的思维方式，培养学生逻辑思考问题的良好思维习惯.

结论

综上所述，中考数学的解题方法是非常丰富和多元化的，学生们在中考前所学校的解题方式也是非常多的。学生们需要掌握的关键一点就是要学会用适当的解题方式去解决具体的数学题目，要确保自己所掌握的解题方式都能够落到实处。

参考文献

[1]韩诗贵.从一道题的常见错误反思课堂教学——以2019年无锡市数学中考第25题为例[J].初中数学教与学，2020（09）：39-41.

[2]付英，廖帝学.有序有道有度——中考数学复习模拟训练阶段的教学分析与构想[J].教学月刊·中学版（教学参考），2020（05）：51-55.

[3]李芸.让数学思维触角自由合理延伸——谈中考数学专题复习[J].中国数学教育，2020（09）：59-64.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。