《相似旋转模型在初中数学解题中的应用》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

相似旋转模型在初中数学解题中的应用

范文

钟育煌

摘要：随着社会的进步，科技也在不断的发展。在科技快速发展的今天，数学学习无疑显得更加重要。因此为了可以培养出更多的理工科专业人才，我们需要加强对初中学生数学知识的培养。在初中数学学习中具有许多的重点与难点，而其中最为重要的便是相似旋转模型的相关概念及其在初中数学解题中的应用。下面，本文将就相似旋转模型在初中数学解题中的应用进行简要介绍。

关键词：相似旋转模型、初中数学、解题、应用

中图分类号：G4? 文献标识码：A? 文章编号：（2020）-48-395

一、相似旋转模型概述

1.1相似旋转模型的概念

为了加强初中同学对相似旋转模型的学习，我们首先需要就相似旋转模型的概念进行简要阐述。相似旋转模型与传统的相似相同均属于初中数学学习过程中极为重要的相似概念之一。通过对相似旋转模型的学习不但可以方便同学们对经过旋转后所形成的两个三角形进行相似的证明，同时还可以得出诸多的结论，从而进一步方便同学们对相似的相关知识进行学习。相似旋转模型这一概念主要是指，将一个三角形按照某一个顶点进行旋转后所得的一个三角形不但其两条边的长度不会进行改变。同时由于其一个三角形是经过另一个三角形按照某一顶点旋转所得，因此两个三角形相邻边之间的夹角均与旋转角度相同。通过对上述这些数据信息进行整合后，我们可以轻松通过两边及一夹角相同，从而证明出旋转后的三角形与旋转前的三角形相似。通过对这一模型进行进一步拓展，我们还可以得出经过旋转后的多边形与原多边形也是相似的。

1.2相似旋转模型的作用

在上文中曾提到，相似旋轉模型在初中数学学习中不但可以方便同学们对三角形以及多边形进行相似证明，同时通过对这一数学模型进行学习还可以得出诸多结论，进而进一步丰富同学们的数学几何知识。除这两点作用外，通过对相似旋转模型的相关知识进行学习还可以方便同学们对绕公共顶点的相似形旋转体进行研究。在初中数学学习中时常可以看到求三角形按某一公共点旋转后所得图形与原图形的夹角以及旋转图形与原图形所结合的面积等问题。在面对这一系列问题时，同学们若通过常规方式进行证明与计算不但需要建立大量的辅助线，同时还极易出现计算错误的现象。而通过对相似旋转模型进行学习，则可以直接利用旋转角等结论，从而求得问题中的角度与面积等信息。另外，通过学习相似旋转模型，也可以方便同学们对对角互补型中的旋转相似进行求证。

二、相似旋转模型在初中数学解题中的应用

相似旋转模型在初中数学解题中的应用大致有以下两个方面，其一是通过使用相似旋转模型从而为相似证明过程中以及角度、面积等求解过程中提供相应的数据信息。另一方面，通过利用相似旋转模型也可以从一定程度上拓宽同学们的辅助线建立方式，从而方便同学们对相似、相等等问题进行证明，同时也可以方便同学们对面积以及角度等信息进行求解。首先，同学们通过使用相似旋转模型可以轻易得知旋转后所得图形与原图形所对应边的长度相等，并且经过旋转后两个图形所对应的角度也是相同的。此外，在面对一些复杂图形时，同学们难免会出现一些没有思绪的现象，而这时其便需要通过建立相应的辅助线从而帮助同学们完成对相关问题的解答与证明。但辅助线的建立也需要一定的学习，好的辅助线可以使同学们提高对相关问题的解答效率，而较差的辅助线不但需要建立多条辅助线，同时也会严重影响到同学们对相关问题的计算效率。而通过相似旋转模型所建设的辅助线，由于其辅助线建设完成后同学们可以获取到一些相关的数据信息，因此通过使用这一方式所建立的辅助线可以极大提升同学们在解决相关几何问题时的计算与证明效率。

三、相似旋转模型在初中数学解题应用中的具体事例

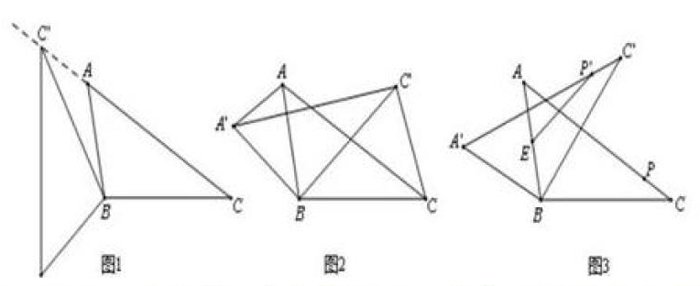
在上文中曾对相似旋转模型的概念及作用进行了简要介绍，下面本文将对相似旋转模型在初中数学解题应用中的具体事例进行简要介绍。例如在△ABC中，AB=4，BC=6，∠ACB=30°，将△ABC绕点B按逆时针方向旋转，得到△A′BC′.

（1）如图1，当点C′在线段CA的延长线上时，求∠CC′A′的度数;

（2）如图2，连接AA′，CC′.若△CBC′的面积为3，求△ABA′的面积;

（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转的过程中，点P的对应点是点P′，直接写出线段EP′长度的最大值与最小值.

在解决这一问题时，若仅仅依靠三角形的相似问题将会耗费大量的时间，同时在计算过程中也极有可能会出现计算失误的现象。但若通过旋转全等的相似模型便可以轻松的求解出相关信息。当同学们在计算第一问时，由旋转的性质可得：∠A′C′B=∠ACB=30°，BC=BC′，又由等腰三角形的性质，即可求得∠CC′A′的度数。而同学们在计算第二问时则可以直接通过相似三角的相关结论进行计算，如由△ABC≌△A′BC′，易证得△ABA′∽△CBC′，然后利用相似三角形的面积比等于相似比的平方，即可求得△ABA′的面积。而同学们在计算第三问时也需要通过利用相似旋转模型进行相关计算。由①当P在AC上运动至垂足点D，△ABC绕点B旋转，使点P的对应点P′在线段AB上时，EP′最小;②当P在AC上运动至点C，△ABC绕点B旋转，使点P的对应点P′在线段AB的延长线上时，EP′最大，即可求得线段EP′长度的最大值与最小值.

四、结束语

综上，本文通过一些初中数学解题例子详细地讲述了相似旋转模型在初中数学解题中的具体应用。在文本的介绍中我们就相似旋转模型的概念展开了深入的研讨，并就相似旋转模型在实际数学解题过程中所起到的作用展开了分析，可以说相似旋转模型是一种数学解题思维中较为常见的解题模式，学生必须充分掌握好这一解题模式，只有能够灵活地应用起这一数学解题原理，在日常解题过程中学会举一反三，才能够真正将这一知识点贯穿于初中数学解题中。旋转的问题有时候并不是仅仅涉及到单一化的旋转，更多地会涉及到一些组合题型，相似、旋转经常会出现在一些大的解题中，一旦学生能够充分掌握二者之间的密切联系，就能够在解题时第一时间想到这一思路，进而为学生后续进一步地学习各种复杂性的旋转相似组合问题奠定一定的知识基础。初中数学教师也要注意改进自身的教学模式，不断鼓励学生在解题过程中养成勤思考、乐于创新的学习习惯，充分发展学生的数学思维，增强应用意识。只有这样在进行后续解题过程中，学生才能够有着明确的思维方向，进而在解题时第一时间弄清题意，有利于深入研究问题，解题过程也将更加简洁明了。

参考文献

[1]张进.一道中考模拟试题的多种解法[J].数理化学习（初中版），2016（11）：47-48.

[2]李世臣.借助相似模型探讨尺规作图[J].数学教学，2016（07）：17-20.

[3]吴俊杰.对一道旋转相似问题数学模型的探究[J].中学数学，2015（16）：96-98.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。