《核心问题引领小学数学课堂走向高效》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

核心问题引领小学数学课堂走向高效

范文

黄燕培

【摘要】都说好的问题能成就好的课堂。而基于学科本质，建立在培养学生的思维基础上，引发学生积极思考、讨论、理解，关注数学核心素养，并对知识的学习，方法的探究，问题的解决起到重要作用的问题就是核心问题。它不但能促进学生的丰富生成，能引领学生的探究活动，更有助于培养学生的数学核心素养，引领课堂走向高效。

【关键词】核心问题;探究活动;核心素养

众所周知，在数学课堂上，一节课的成败往往取决定于一两个关键问题的设计与处理，从孔子的“启发式教学”到苏格拉底的“产婆术”，都是把问题设计作为数学的核心技术来重视的。而在张奠宙教授提出数学教育的四条特有原则：数学化、适度形式化、问题驱动、提炼数学思想方法中，也把“问题驱动”作为一种重要的数学教学策略。的确，好的问题能成就好的课堂。怎样的问题才是好问题？我认为它应具有如下特点：基于学科本质，建立在培养学生的思维基础上，引发学生积极思考、讨论、理解，关注数学核心素养，并对知识的学习，方法的探究，问题的解决起到重要作用——也就是一节课的核心问题。它不但能促进学生的丰富生成，能引领学生的探究活动，更有助于培养学生的数学核心素养，引领课堂走向高效。

一、核心问题促进学生的丰富生成

课堂的生成，是指教师在备课过程中没有预设到的学生的独特设想或见解。而这些设想或见解，大多是从学生的认知出发，相比于教师的预设或讲解，更能让大部分学生接受。所以，这些丰富的生成，是进行课堂探究的宝贵资源。合理地引导和使用能使我们的数学课堂充满灵动和活力。但是，这样的生成，不是在任何时刻都能产生的，往往需要教师的引导，在某种特定的情形下才能从学生的思维中“闪现”出来。

1.直面知识本质的生成

案例一：

如，在学习人教版五年级上册《小数除法》这一单元的《除数是小数除法》时，教师一开始并不是采用“复习除数是整数的除法——引导学生把除数是小数的除法转化成除数是整数的除法——归纳方法”这一套路，而是提出了具有思考性的核心问题“除数是小数的除法可能以用什么方法解决？”并以“8.75÷2.5”为例，让学生进行独立尝试。由于教师有足够的时间让学生进行思考，造就了学生精彩的生成，请看：

生1：8.75÷2.5=（8.75×2）÷（2.5×2）=

17.5÷5=3.5

生2：8.75÷2.5=（8.75×10）÷（2.5×10）=

87.5÷25=3.5

生3：8.75÷2.5=（8.75×4）÷（2.5×4）=

35÷10=3.5

生4：8.75÷2.5=（8.75×100）÷（2.5×100）=875÷250=3.5

生5：竖式计算

这些精彩的生成，打破了以往课堂上把“发现转化”作为教学重点，而是让学生通过独立思考，在学习了“除数是整数的小数除法”的基础上，从自己的认知出发，直面知识的本质，找出不同的方法。这些生成将是下面进行课堂探究的宝贵资源。而这些生成，都是源于教师的“除数是小数的除法可能用什么方法解决？”这一核心问题的引领。

2.探究解题策略的生成

案例二：

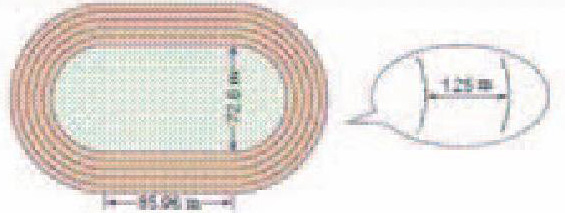
又如在学习人教版六年级上册《确定起跑线》这一内容时，教师也同样采用核心问题引导学生丰富的生成：

【案例2】

学生认识了跑道的结构后……

师：怎样找出相邻两个跑道的长度之差？

学生独立思考，并尝试解决：

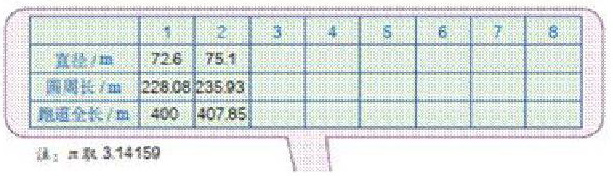
生1：我分别把每条跑道的长度算出来，也就是计算2个直道长度与一个圆周长的总和，再相减，就可以知道相邻两条跑道的长度之差。

生2：因为跑道的长度与直道无关，只要计算出各圆的周长，再算出相邻两圆的周长相差多少米，就是相邻跑道的长度之差。

75.1×3.14159-72.6×3.14159≈7.85（m）;

77.6×3.14159-75.1×3.14159≈7.85（m）;

……

生3：先求弯道直径之差，再计算长度之差。

（75.1-72.6）×π=2.5π≈7.85（m）;

（77.6-75.1）×π=2.5π≈7.85（m）;

……

在这里，教师利用“怎样找出相邻两个跑道的长度之差？”作为核心问题进行引领，并给学生足够的时间进行独立思考、探究，形成自己对问题的想法，于是，生成了不同的解决策略。

从上面两个例子，课堂之所以精彩不断，源于课堂学生精彩的生成，而学生的精彩生成，有赖于教师核心问题的引领，两者相辅相成，而在此过程中，学生一直处于探究、思考的高峰，学生的思维一直处于活跃的状态，课堂一直处于不斷的探究，最后问题得以顺利解决，成就了有效的课堂。

二、核心问题引领学生开展探究学习

《数学课程标准》提出：“有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式”。所以作为一线教师，也应该用更多的精力去关注、思考、实现数学课堂上学生学习方式的转变。但是，课堂上我们该如何引导学生进行探究学习？——可尝试用核心问题去引领。

1.用核心问题引导学生进行类比、猜想、推理、验证

案例三：

我们来看看人教版六年级上册的《比例的基本性质》——

课始，教师提问：你们还记得商不变的规律和分数的基本性质吗？结合学生的回答，教师呈现了商不变的规律和分数的基本性质，并齐读。接着再出现：6：8=6÷8=、12：16=12÷16==。请你联系比和除法、分数的关系，想一想：在比中有什么样的规律？当学生想不得法时，教师还利用下面的关系图进行了提示：

很快，比的基本性质顺利地小结出来。

显然，上述案例中，教师没有进行死塞硬套，而是一步一步地引导学生从已有知识走向未知知识，最后达到目的。教师设计的问题也是亦步亦趋“你们还记得商不变的规律和分数的基本性质吗？→比和除法、分数的关系？→利用知识的迁移小结出比的基本性质”。这个教学的过程，教师一步一步把学生引向教学目标，顺利达到教师想要的预期效果。但是，反思这样的教学过程，我们会发现问题——学生只是被动地接受，学生没有参与探究过程，那么他们对所学的知识真的掌握吗？实践证明，这样学习，学生对“比的基本性质”是理解不深，掌握不牢。一旦遇到一些针对概念的似是而非的判断题，或是应用性质进行化简比，这个缺点就会显现出来。而且，学生漫长的学习过程中，存在很多不确定的因素，是否每次教师都要为他们做好铺垫，清除障碍，做好充分的准备呢？这样的学习学生还有多少灵活性？能动性？还有什么学习能力可言？于是我采用“核心问题”引领，对教学过程作了以下的调整：

课始，教师：我们知道，比与除法、分数之间存在着极其密切的联系，而除法具有商不变性质，分数有分数的基本性质，联想这两个性质，想一想：在比中又会有怎样的规律或性质？提出问题后，学生在各自的认知水平上，纷纷猜想比的基本性质。根据学生的猜想教师板书：比的前项和后项同时乘或除以相同的数（0除外），比值不变。

至此，似乎是水到渠成，但是，教师在此再进一步提出问题：正如大家想的，比和除法、分数一样，也具有属于它自己的规律性质，那么是否和大家猜想的“比的前项和后项同时乘或除以相同的数（0除外），比值不变”一样呢？这需要我们通过研究证明。接下来，请大家分成四人小组合作学习，共同研究并验证之前的猜想是否正确。

探究学习由此产生：（1）学生独立完成：写出一个比，并用自己喜欢的方法进行验证。（2）小组讨论学习。①每个同学分别向组内同学展示自己的研究成果，并依次交流（其他同学表明是否赞同此同学的结论）。②如果有不同的观点，则举例说明，然后由组内同学再次进行讨论研究。③选派一个同学代表小组进行发言。（2）集体交流（要求小组发言代表结合具体的例子在展台上进行讲解）。有的学生根据比与除法、分数的关系进行验证;有的学生根据比值验证。（3）全班通过具本算式进行验证：10：15=10÷15==、15：9= 15÷9=、16：20=（16○□）：（20○□）题中○内可以怎样填？□内可以填任意数吗？为什么？学生发表自己的见解并说明理由，教师完善板书。（4）完善归纳，概括出比的基本性质。

在此过程中，教师先以“比与除法、分数之间存在着极其密切的联系，想一想：在比中又会有怎样的规律或性质？”作为核心问题，引领学生进行猜想。当猜想生成后，教师又以：那么是否和大家猜想的“比的前项和后项同时乘或除以相同的数（0除外），比值不变“一样呢？这需要我们通过研究证明。——这一问题引导学生进行验证。而这证明的过程，其实就是学生很好地理解“比的基本性质”的过程，由于学生亲历“知识的形成—验证—总结”，理解了知识的本质，不但对“比的基本性质”理解深刻，学生的思维得到了发散，课堂是学生真正自主探究的课堂，学习是真正体现以学生为主体的学习。我想，这样的学习，对学生来说才是真实、有效的。

2.用核心问题引导学生的开展实践探究

案例四：

如，人教版六年级下册的实践活动课《自行车里的数学》，就是探究自行车里蕴含的数学问题。内容比较抽象，单凭纸上谈兵，不经历操作，观察，思考，学生很难理解自行车运行的原理，于是教师采取用问题引领学生进行探究？

课前，先布置实践作业，让学生回家“玩自行车——观自行车——思自行车”，并设计几个对应用的问题 “你们知道自行车是怎样前进的吗？”“是前齿轮带动自行车前进还是后齿轮？”“你的自行车前齿轮有几个齿，后齿轮有几个齿？”，让学生自主探究。

课中，当学生弄清楚前面的问题后，教师抛出了“前、后齿轮的齿数与它们的转数什么关系？”“前轮转动一周，后轮转动多少周？”“蹬一圈的路程怎样算？”这三个问题形成问题链，层层递进，将学生的探究推向高涨，引向深入。特别是 “前轮转动一周，后轮转动多少周？”这一核心问题，学生争议最大。这时教师适时地让学生把各自体验和观察到的在小组交流并讨论，给予学生一个把生活中的问题转变到数学学习的空间和平台。学生通过探究交流后，再结合多媒体课件有关链条的动态演示（如上图）。学生很容易明白到：前齿轮和后齿轮的齿通过链条带动，前齿轮转过一个齿，后齿轮就转过一个齿，这说明了前齿轮和后齿轮转过的总齿数是相同的，即齿数和转数成反比例关系，并归纳出：前齿轮的齿数×转数=后齿轮的齿数×转数，再结合自己的实践经验，学生明白到自行车是以后轮带动前进的，从而推导出瞪一圈自行车走的距离=车轮的周长。

这一探究过程，环环紧扣，利用问题串把探究的热情推向高潮，又以“前轮转动一周，后轮转动多少周？”这一核心问题，把探究推向深入，最后得以解决問题，而教师在学生探究过程中，关注学生的学习状态并注意引导学生点拨，教学效果显而易见。

三、核心问题有助于培养学生的核心素养

如果说核心问题是推进课堂学习的动力，那么学生的数学核心素养是在不断地发现问题和解决问题的过程上得以培养的。那么什么是数学的核心素养？著名的学者张奠宙教授这样理解：数学的核心素养包括“真、善、美”三个维度——理解理性数学文明的文化价值，体会数学的严谨性、精确性; 具备用数学思想方法分析问题和解决实际问题的基本能力;能够欣赏数学智慧之美，喜欢数学，热爱数学。那么，课堂上我们怎样结合知识进行核心素养的培养呢？

1.回顾案例一 ——引导学生对所获得的对数学知识本质的理解和掌握

在刚才的【案例一】中，教师提出了“除数是小数的除法可能用什么方法解决？”这一核心问题，并让学生以“8.75÷2.5”为例尝试解决。学生通过独立思考，很快想到了以下的不同方法，在此基础上，教师让学生小组交流后，再个别学生进行分析：

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。