《从一道高考题的变迁看阿基米德三角形性质及其定理的演绎》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

从一道高考题的变迁看阿基米德三角形性质及其定理的演绎

范文

李真徐水龙

【摘要】阿基米德三角形有着丰富的内涵、深刻的背景，至今依然是高考命题者的青睐，其有关性质仍是命题专家的热点素材.本文从一道2008年山东高考题开始，探索阿基米德三角形定理的由来，演绎其性质应用.

【关键词】阿基米德三角形定理;性质演绎

阿基米德是古希腊伟大的物理学家、数学家、天文学家和机械发明家.抛物线的弦与过弦的端点的两条切线所围成的三角形，常被称为阿基米德三角形.阿基米德三角形以其丰富的内涵、深刻的背景，在数学发展的历史长河中不断发出闪耀的光芒，至今依然是高考命题者的青睐，其有关性质也成为命题专家的热点素材.下面举例说明.

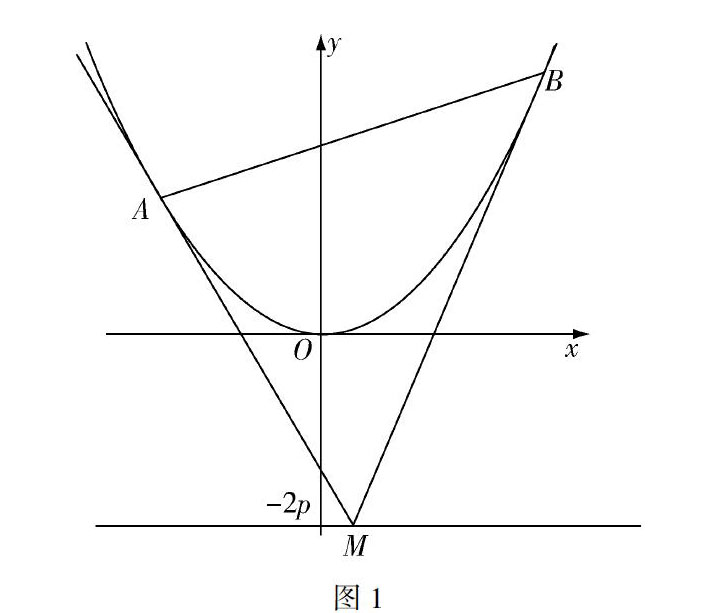
这是2008年理科第22题（部分）.如图1，设抛物线方程为x2=2py （p>0），M为直线 y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B.求证：A，M，B三点的横坐标成等差数列;

本题涉及阿基米德三角形，考查了阿基米德三角形的有关性质.

（1）求直线AB与y轴的交点N的坐标;

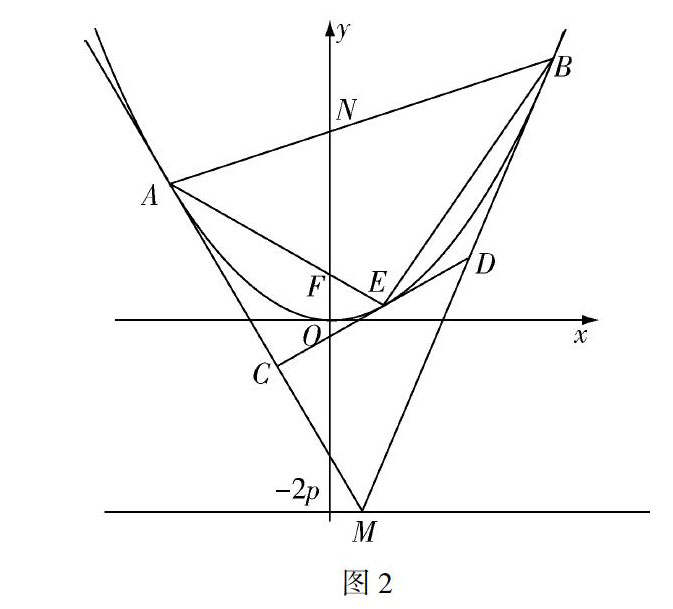
（2）若E为抛物线弧AB上的动点，抛物线在E点处的切线与△MAB的边MA，MB分别交于点C，D，记λ=S△EABS△MCD，问：λ是否为定值？若是，求出该定值;若不是，请说明理由.

问题（1）求直线AB与y轴的交点坐标，由前面分析可知直线AB的方程，我们只需令y=0即可，直线AB与y轴的交点坐标为N（0，2p），是个定点.于是我们猜想弦AB绕着N点转动，M点的轨迹是什么？我们设M（x，y），有x=x1+x22，y=x1x22p，由A，N，B三点共线，得y=-2p，显然它是一条直线.我们进一步猜想弦AB绕着点G（xG，yG）转动，M点的轨迹是什么？由A，G，B三点共线，得（x1+x2）xG-2pyG-x1x2=0，将x1+x2=x，x1x2=y代入，得xGx-p（y+yG）=0，它仍然是一条直线.于是我们得到阿基米德三角形的性质2.

性质2 若阿基米德三角形的底边AB过抛物线内定点G（xG，yG），则另一顶点M的轨迹为一条直线，其方程为xGx-p（y+yG）=0.

特别地，当定点G在y轴上时，性质2还有以下推论.

阿基米德三角形定理抛物线和它的一条弦所围成的封闭图形的面积，等于抛物线的弦与过弦的端点的两条切线所围成的三角形面积的三分之二.

阿基米德三角形背景深刻，内涵丰富，我们从一道高考题演绎了阿基米德三角形的性质及其定理.

【参考文献】

[1]方亚斌.千年古图蕴藏题库：阿基米德三角形演绎高考题[J].中学教研（数学），2017（7）：33-39.

[2]邵志明，陈克勤.高考試题中的阿基米德三角形[J].数学通报，2008（9）：39-46.

[3]刘瑞美.对一道2011年高考圆锥曲线问题的探究[J].数学通迅，2012（5）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。