《微课在高中数学教学中的应用探析》-教育论文，课程教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

微课在高中数学教学中的应用探析

范文

闫澍

【课题】本文是2018年甘肃省教育科学规划课题《高中数学微课应用初探》阶段性研究成果，课题立项号：GS〔2018〕GHB3016。

【中图分类号】G633.6;【文献标识码】A 【文章编号】2095-3089（2020）07-0176-02

数学新课程标准中增加了数学核心素养的概念，其实纵观新课程标准，对数学的学习要求无非是爱好数学，学好数学，用好数学，下面我结合微课应用谈几点教学体会。

;微课的特点：①短小、精炼，学生可利用零碎时间学习。②不受时空限制，学生可随时随地学习。③集聲音、视频、图片、文字为一体，可更好提高兴趣。基于上述特点，我尝试着在如下三个方面应用取得较好的效果。

一、课前预习，精心设计问题与学法指导

高中数学难度大，跨度大，课前预习的重要性不必多说，但有些同学缺乏课前预习的好习惯，或者说预习什么？怎么预习？预习到什么程度？一片茫然，无从下手，为指导、帮助学生养成预习习惯，提高预习能力，要求发授的微课能调动学习兴趣，激发欲望，所以从两个方面考虑设计微课，一是设计好的引例、问题，二是给予学法指导。

例如在学习《三角函数》一章，先发布两个问题：

微课一：

问题一：同学们对照日历看一下，4月某日与7月同日分别是星期几？有什么关系？这是巧合吗？还有几月几日的日期与星期有这种关系？

问题二：2019年5月1日是星期三，去年的5月1日是星期几？明年的5月1日是星期几？

微课二：

讲评：问题一

4月某日与七月同日相差91天，91÷7=13，正好除尽。所以星期几相同。

问题二：今年5月1日与去年5月1日相差365天，365÷7=52…1，所以，今年的5月1日星期几比去年的迟一天，于是去年的5月1日为星期二。

同学们计算明年与后年的5月1日是星期几？

结论：这两个问题是相同的，涉及两个变量，日期与星期，而每星期只有7天，所以当日期在不断变化时，于是星期重复出现，数学上称这种变化为周期性变化。生活中这样的例子很多，而且有很多成语就是说周期性变化的，同学们自己搜集。而诱导公式一与周期函数定义都是这样，这是本章中的一个重点。

微课一可以是纯文件，也可以以文本插入日历背景。微课二，由教师讲述，可适当补充内容，录为视频，也可以录为纯文本，时长约4min。

高中数学各章都有其特点，学习内容不同，学习方法也有侧重点，可以在预习中指出本章或本节的学习方法，使学生学习有法可依，对提高自学能力帮助很大。

二、课堂讲授中重视思想方法与思维训练

学习数学的目的有三方面：一是学习数学知识，二是掌握思想方法，三是锻炼思维能力。思想方法属于思维范畴，是一种意识形态，数学知识只是一种载体，通过学数学知识而学习思想方法，一旦学好、用好了这些方法，会终身受益。

高中数学中用到的思想方法共有十多种，而最常用的有四种，即函数与方程，数形结合，分类与整合，转化与化归，而且后两种在其他学科中、生活中也经常使用。所以在平时上课时要不断渗透这些方法，应用这些方法，使学生通过平时学习理解，掌握并应用，逐步发展学生的数学意识。

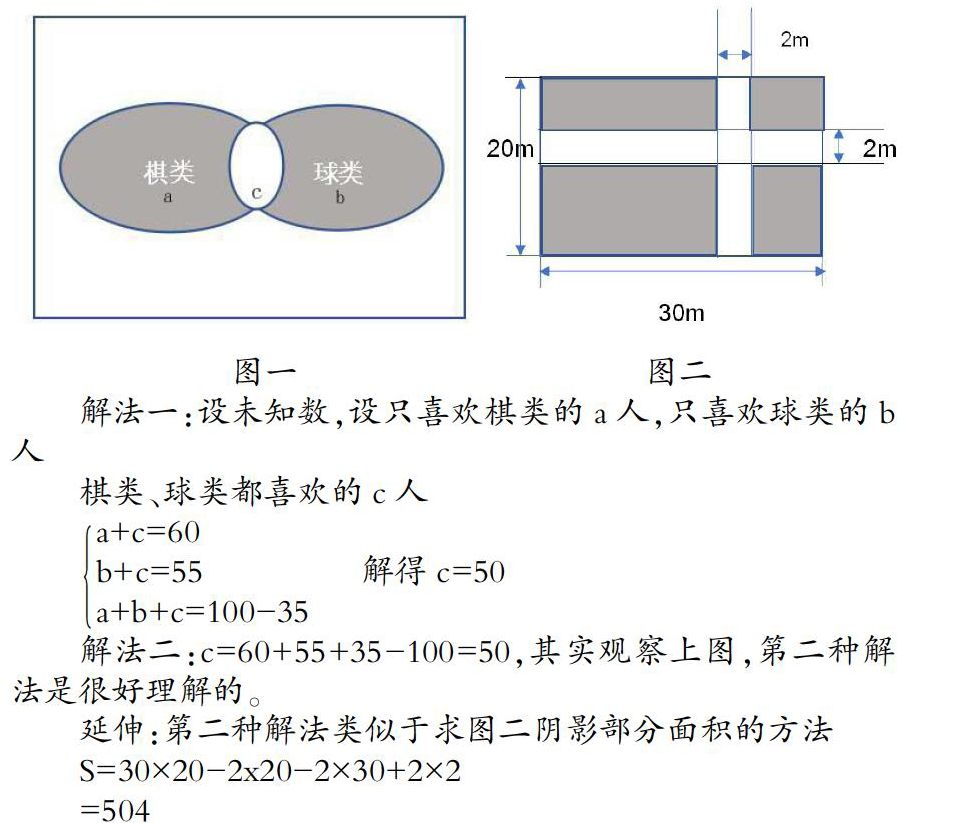
例如：Venn图法学生一般不太习惯用，其实这是数形结合的最好方法。

微课三：某学校少年宫有100人，其中有60人喜欢棋类活动，55人喜欢球类活动，而喜欢书法的既不喜欢球类又不喜欢棋类有35人，问同时喜欢棋类和球类的有多少人？

分析：展示Venn图

解法一：设未知数，设只喜欢棋类的a人，只喜欢球类的b人

棋类、球类都喜欢的c人

a+c=60b+c=55a+b+c=100-35解得c=50

解法二：c=60+55+35-100=50，其实观察上图，第二种解法是很好理解的。

延伸：第二种解法类似于求图二阴影部分面积的方法

S=30×20-2x20-2×30+2×2

=504

这类题目在小学初中都已学习过，让学生体会一下。

数形结合能把抽象的数学语言用图形表示出来，化抽象为具体，化繁为简，化难为易，这在培养学生思维的灵活性，分析能力方面有很好作用。

三、课后辅导多方面并举，鼓励引导学生自己发布微课

课后辅导是课堂的延伸，一方面能把课堂的未消化问题及时解决，另一方面拓展视野。课后辅导可以根据需要不定期的发布微课，从多方面入手，例如概念辩解、难点透析、规律方法、知识延伸、趣味数学（数学史话，超前学习<例如在第一学期发布倒序相加法与错位相减法、思维训练题、生活中的数学>）、章节小结（本章知识流程图或结构图、本章思想方法归纳、本章学习反思与感悟）等，以专题发布，发布形式多样性，可以是视频、图片、文本或其结合，旨在提高学习深度、广度，拓展视野，提高兴趣，培养数学能力。

微课四：函数单调性证明方法

基本步骤：取值→作差→变形→定号

难点：变形→定号

原理：一个代数式当各项同号时可判断正负，各项异号时不能判断正负;而如果能分解因式又能判断各因式符号则可判断正负。

规律方法：

1.作差后为整式时，分解因式或配方。

2.作差后为分式时，通分。

3.作差后为根式，分子有理化，使分母为正，分子为整式。

;此节微课此处略掉例题，实际应用时加上例题约需8min，直接以视频配幻灯片。

为学生提供平台，鼓励学生将自己在学习过程中的疑问、经验、感悟、得失，一题多解，变换条件解答等等发布出来，相互交流讨论。

上述微课是笔者在教学中发布使用过的，实践证明，经过近两年的微课应用，学生在自主学习、阅读能力、思想方法掌握应用、学习兴趣等方面得到了一定的改善。

问卷调查表明：①95%的学生能及时接收微课并学习。②83%的学生认为微课对自己学习有较大帮助。③40%的学生能将部分内容反复阅读并整理归纳。④36%的学生对“趣味数学”更感兴趣，能在班级群或课间讨论。⑤60%的学生认为通过预习能减轻课堂负担，轻松听课。⑥最受欢迎的是课前预习中的引例设计与学法指导。

总之，微课在提高自学能力，学习兴趣等方面有较大的作用，教师在教学中要根据需要设计、应用好微课，经常用、坚持用，全面提高学生数学核心素养，为高中数学教学服务，为学生终身发展奠定基础。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。