《数学模型在财经专业课程中的案例研究》-教育论文，职业教育论文-论文范文参考-科学狗论文网

标题

数学模型在财经专业课程中的案例研究

范文

庄春

[摘 ? ? ? ? ? 要] ?在财经类院校中，学生数学学习的好坏将会影响到一些专业课的学习，因为在一些专业课中，有一些知识是需要用到数学模型的。试通过对四个案例的研究，阐明一些数学模型在专业课中的一些应用，对研究高职数学课与专业课结合教学具有一定的指导价值。

[关 ? ?键 ? 词] ?数学模型;财经专业;案例研究

[中图分类号] ?G712 ? ? ? ? ? ? ? ? ? [文献标志码] ?A ? ? ? ? ? ? ? ? ? ?[文章编号] ?2096-0603（2019）18-0118-02

高职数学是各个高职院校的一门基础课程，无论何种专业，数学都是培养学生整体素质不可或缺的一门学科。数学对其他课程的学习有着举足轻重的作用，尤其对财经专业来说更是如此，在一些财经专业的课程中运用到了各种数学模型。本文将从四个案例来探讨数学模型在会计专业课中的应用。

一、指数型函数、对数函数模型

对数函数是高职数学中一个重要的内容，在学习过程中，学生对对数概念的学习比较困难，也比较枯燥，对数函数在实际生活中有着广泛的应用，同时在财务管理专业课程中也有应用。在指数型函数中，求指数的问题往往可以转化为利用对数的转化公式，可以通过求对数来求出指数。在财务管理这门课程中，在资金时间价值的应用这一小节里，已知普通年金现值系数■，i为年利率，要求期数n，这里就需要用到对数函数的计算公式了。

例题：某单位计划引入一台蒸汽机来替代目前使用的燃气机，蒸汽机的价格比燃气机高2000元，但每年可节约燃烧成本500元，若利息率为10%，则蒸汽机需要使用多少年此次替代才有利？

解：根据题意，普通年金现值系数为■=4，则■=4，i=10%，

代入公式，得1.1n=■，根据对数计算公式，n=■≈5.36（年）.

一般来说，在指数型函数中，求指数是比较困难的，只有利用对数函数的计算来求指数，才能较便捷地求出指数。

二、线性规划模型

在管理会计这门专业课中，经常会遇到这样的问题：如何合理安排有限的人力、财力、物力等资源，使这些资源的效能得到充分地发挥，以获取最佳的经济效益。要解决这类问题，最常用的方法就是运用数学中的线性规划模型。线性规划问题的数学模型有以下三个特征：（1）每一个问题都用一组决策变量来表示，这些变量一般情况下取非负值;（2）存在一定的约束条件，通常用一组一次（线性）不等式或等式表示;（3）都有一个要达到的目标，用决策变量的一次（线性）函数即目标函数来表示，按问题的不同实现最大化或最小化。

满足以上三个条件的线性规划数学模型的一般形式为：

目标函数max（min）z=c1x1+c2x2+…+cnxn.

约束条件a11x1+a12x2+…+a1nxn≤（=，≥）b1a21x1+a22x2+…+a2nxn≤（=，≥）b2 ? ?…………am1x1+am2x2+…+amnxn≤（=，≥）bm ? x1，x2，…xn≥0

例题：一早餐店要做A、B两种包子，A种包子的主要原料是每3份糯米粉加2份小麦粉，B种包子的主要原料是每4份糯米粉加1份小麦粉。这个早餐店每天可买进糯米粉50kg、小麦粉20kg，做1kgA种包子的利润是5元，做1kgB种包子的利润是4元，那么这个早餐店每天各做多少个A、B两种包子才能获利最多？

解：设A、B两种包子计划产量分别为xkg，ykg，利润为z元，则z=5x+4y.

由题可得，约束条件为3x+4y≤250，2x+y≤100，x≥0，y≥0，目标函数maxz=5x+4y.

解得x=30y=40，于是得到目标函数的最优解为maxz=5x+4y=310.

线性规划就是把实际问题归结为一种数学模型，在满足一组约束条件下，求一组决策变量的值，使预定的目标达到最优即求最大值或最小值。

三、矩阵模型

用矩阵解决管理会计中的一些复杂的计算问题，如一些线性的且未知数个数较多的问题。

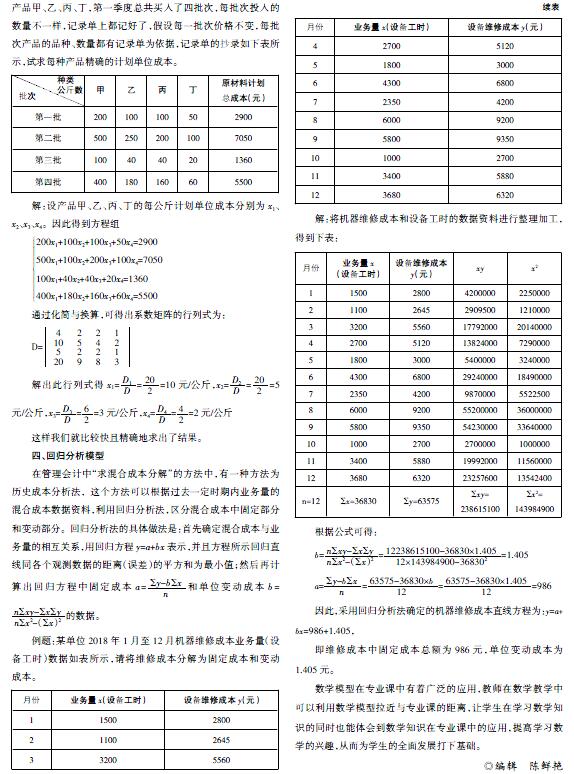
例题：宏达公司买入一种原材料进行生产，可同时产出四种产品甲、乙、丙、丁，第一季度总共买入了四批次，每批次投入的数量不一样，记录单上都记好了，假设每一批次价格不变，每批次产品的品种、数量都有记录单为依据，记录单的抄录如下表所示，试求每种产品精确的计划单位成本。

解：设产品甲、乙、丙、丁的每公斤计划单位成本分别为x1、x2、x3、x4。因此得到方程组

200x1+100x2+100x3+50x4=2900500x1+100x2+200x3+100x4=7050100x1+40x2+40x3+20x4=1360400x1+180x2+160x3+60x4=5500

通過化简与换算，可得出系数矩阵的行列式为：

D=■

解出此行列式得x1=■=■=10元/公斤，x2=■=■=5元/公斤，x3=■=■=3元/公斤，x4=■=■=2元/公斤

这样我们就比较快且精确地求出了结果。

四、回归分析模型

在管理会计中“求混合成本分解”的方法中，有一种方法为历史成本分析法，这个方法可以根据过去一定时期内业务量的混合成本数据资料，利用回归分析法，区分混合成本中固定部分和变动部分。回归分析法的具体做法是：首先确定混合成本与业务量的相互关系，用回归方程y=a+bx表示，并且方程所示回归直线同各个观测数据的距离（误差）的平方和为最小值;然后再计算出回归方程中固定成本a=■和单位变动成本b=■的数据。

例题：某单位2018年1月至12月机器维修成本业务量（设备工时）数据如表所示，请将维修成本分解为固定成本和变动成本。

解：将机器维修成本和设备工时的数据资料进行整理加工，得到下表：

根据公式可得：

b=■=■=1.405

a=■=■=■=986

因此，采用回归分析法确定的机器维修成本直线方程为：y=a+bx=986+1.405，

即维修成本中固定成本总额为986元，单位变动成本为1.405元。

数学模型在专业课中有着广泛的应用，教师在数学教学中可以利用数学模型拉近与专业课的距离，让学生在学习数学知识的同时也能体会到数学知识在专业课中的应用，提高学习数学的兴趣，从而为学生的全面发展打下基础。

编辑陈鲜艳

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。