《对高职数学函数极值和最值的教学过程研究》-教育论文，职业教育论文-论文范文参考-科学狗论文网

标题

对高职数学函数极值和最值的教学过程研究

范文

[摘 ? ? ? ? ? 要] ?函數极值是高等数学中一个重要的基本概念，是学习最值的重要基础.通过直观教学法、问题驱动法、案例教学法等设计教学过程，改进高职数学函数极值和最值的传统教学过程，将函数的极值和最值统一进行教学。

[关 ? ?键 ? 词] ?函数极值;驻点;极值点;最值

[中图分类号] ?G712 ? ? ? ? ? ? ? ? [文献标志码] ?A ? ? ? ? ? ?[文章编号] ?2096-0603（2019）30-0062-02

一、前言

函数的极值是高等数学中一个重要的基本定义，作为初等函数的重要内容之一，它既是函数导数的进一步应用，又是学生后续学习函数最值的基础.高职院校学生由于数学功底薄弱，深刻理解函数极值和应用往往存在一定的困难，尤其是函数极值点与驻点关系和实际问题中的最值问题.本文是在传统教学基础上采用直观教学法、问题驱动法、类比法等多种教学方法设计教学过程.学生学习时采用探究式、自主式和合作式的学习方式，这样的设计既有利于培养学生的数学思维，分析问题、解决问题的能力及探索合作精神，又能使学生深刻体会数学中局部与整体的辩证关系，从而使学习高等数学更有成就感.

二、教学过程研究

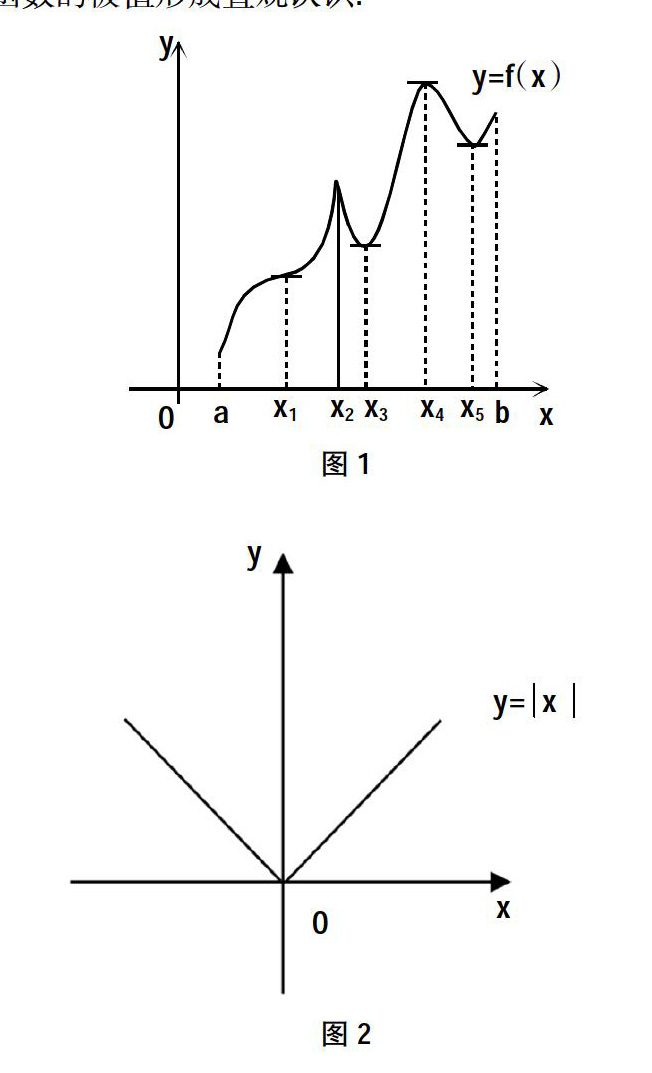
首先，教师借助多媒体展示山势连绵起伏的图片并提示学生观察山峰和山谷的地势特点.接下来展示以下图形，并告知学生函数的极值研究的就是函数图像的“山峰”和“山谷”问题，使学生对函数的极值形成直观认识.

学生观察图1的函数图像并思考：函数图像在点x1，x2，x3，x4，x5处的函数值与其近旁的点的函数值对比有怎样的大小关系.学生仔细比较观察不难发现，f（x2）、f（x4）对应的函数值都比其近旁的函数值大，f（x3）、f（x5）对应的函数值都比其附近的函数值小.此时，教师引入函数极值的概念，即：

定义1：设函数在区间（a，b）内有定义，x0∈（a，b），如果对x0两侧近旁的任意点x（x≠x0），均有f（x）f（x0）成立，则称f（x0）是函数f（x）的一个极小值，x0点称为f（x）的极小值点.

分析理解极值定义，学生很容易判断出f（x2）、f（x4）为极大值，f（x3）、f（x5）为极小值.接着教师引导学生总结得到：只要函数图像出现“山峰”的形状就可以出现极大值，出现“山谷”的形状就可以出现极小值，并且得出函数的极值一定出现在区间内部，在区间端点处不能取到极值.随即教师继续提出问题：极大值是不是一定比极小值大？在一个区间上极值是否是唯一的？学生通过对比讨论图1中的点x2和x5的函数值便可得到答案是否定的，并且能体会到函数在一个区间上的极值可以有多个.接着教师引导学生回忆函数曲线在某点的切线知识，提出问题：函数在以上极值点处的切线斜率有什么特点？学生通过分组讨论探究不难发现：函数在取得极值处的切线往往是水平的，即切线斜率为零.从而，教师引入驻点的定义.

定义2：使f'（x）=0的点称为函数的驻点.

如图1中的点x1、x3、x4和x5处均是驻点，但是并非所有的驻点均取到极值，如点x1.同时，教师引导学生观察点x2可以发现：在有垂直切线的点处也可以取到极值.进一步，教师引入的图像y=x（图2），显然，x=0是此函数的极小值点，但是在x=0处不可导.最后，学生可以总结出：对一个连续函数f（x），在极值点处切线是水平的、垂直的或者切线不存在的，即极值点必是驻点或不可导点，但是驻点和不可导点不一定是极值点.教师提问：函数的驻点和极值点到底有怎样的必然关系呢？学生经过思考后便可以得到极值的必要条件：

定理1：设函数f（x）在点x0处可导且取得极值，则必有f'（x）=0.

以上定理可以简述为：可导函数的极值点一定是驻点，但是驻点不一定是极值点，学生通过观察函数y=x3的图像可知：驻点并不是其极值点.那么，教师继续发问：在没有函数图像的情况下，如何确定一个可能极值点是否为极值点呢？学生根据图1，联系函数的单调性便很容易理解极值的第一充分条件.

定理2：设函数f（x）在点x0的某个空心邻域内可导.

（1）如果当x取x0左侧邻域的值时，恒有f'（x）>0;当x取x0右侧邻域的值时，恒有f'（x）<0，那么函数f（x）在点x0处取得极大值f（x0）.

（2）如果当x取x0左侧邻域的值时，恒有f'（x）<0;当x取x0右侧邻域的值时，恒有f'（x）>0，那么函数f（x）在点x0处取得极大值f（x0）.

（3）如果在x的两侧，函数的导数符号相同，那么函数f（x）在点x0处不取得极值.

接下来，教师采用下列例题与学生一起熟悉极值的判定过程.

教师引导学生书写求解的过程，不仅复习了函数单调性的判断方法，而且将极值的第一充分条件理论转化为实践，加深对定理的理解运用.此外，采用列表法求解清晰简练，能使学生深刻体会数学的简洁美.紧接着，教师指出函数极值的判断除了可以用函数的一阶导数f'（x）判断外，还可以用函数的二阶导数f''（x）来判断.如果f（x）在驻点x0处的二阶导数f''（x0）存在且不为零，则可用极值的第二充分条件判断x0是极大值点还是极小值点.教师提示学生可根据图1中极小值点x3和极大值点x4附近函数图像切线的斜率变化即一阶导数f'（x）的单调性来理解极值的第二充分条件.

定理3：设x0为f（x0）的驻点，即f'（x0）=0，但f''（x0）≠0，则

（1）当f''（x0）>0时，x0为极小值点;

（2）当f''（x0）<0时，x0为f（x）的极大值点.

值得注意的是，如果f'（x0）=0且f''（x0）=0，则x0点可能是也可能不是极值点，这时仍需用定理2来判定，所以定理3虽然判断的过程比较简单，但是相对于定理2而言应用有一定的局限性.对定理2的理解，教师可指导学生通过以下例题分组自行讨论解决.

例2：求函数f（x）=2x3-6x2-18x-10的极值.

解：f（x）在（-∞，+∞）内均可导，且

f（x）=6x2-12x-18=6（x2-2x-3）=6（x-3）（x+1）

令f'（x）=0得駐点为：x1=1，x2=3

且f''（x）=12x-12，

由于f''（-1）=-24<0，故x=-1是函数的极大值点，极大值为f（-1）=0，

由于f''（3）=24>0，故x=3是函数的极小值点，极小值为f（3）=-64.

函数极值在实际生活中有着广泛的应用.利用函数极值可以解决在一定条件下成本最少、利润最大、原材料最省等问题，这些问题反映在数学上就是求函数的最值问题.函数的最大值和最小值统称为最值.教师继续引导学生观察图1并提问函数y=f（x）在区间[a，b]上的最大值和最小值出现在哪里？学生通过观察很容易发现函数y=f（x）在区间[a，b]上的最大值和最小值分别在点x4和a处取到，其中，x=a是区间的左端点，x=x4是极大值点.接着教师指出最值和极值最明显的区别：最值是整个区间上的所有函数值中最大和最小者，它是一个全面、整体性概念.再根据闭区间上连续函数的性质，闭区间上的连续函数最大值和最小值可以在闭区间的内部取到也可以在区间的两个端点处取到，教师引导学生一起总结归纳出函数在区间[a，b]上求最值的步骤：（1）求出f（x）在区间[a，b]上的所有驻点和不可导点;（2）求出驻点、不可导点及区间端点所对应的函数值;（3）对以上函数值比较大小，其中最大的即为最大值，最小的即为最小值.此时教师可安排学生自己求解函数f（x）=x3-x2-2x+3在[2，6]上的最大值和最小值作为课堂练习.

最后，教师需要特别指出的是：函数f（x）在一个区间（有限或无限，开或闭）内可导且只有一个驻点x0，并且此驻点是f（x）的极值点，那么，当f（x0）是极大（小）值时，f（x0）就是f（x）在该区间上的最大（小）值.往往在实际问题中，由实际经验可知，函数f（x）在定义的区间内部的确有最大值或者最小值，而此时只有唯一的一个驻点，就可以判断f（x）在唯一驻点处取得相应的最大值或者最小值.但是，对此理论，有一部分高职学生理解不够深入，教师可以跟学生一起探讨如下例题.

例3：用铁皮做成一个容积一定的圆柱形无盖容器，忽略材料厚度的情况下，问应当如何设计，才能使得用料最省？

以上教学过程设计充分地体现了数形结合思想，通过简单的图形将众多抽象的数学知识形象表现出来，使学生亲身感受数学的应用价值，从心灵上感知数学来源于生活，又回归到生活，激发数学学习的兴趣，增强对数学学习的认同感.

参考文献：

[1]王艳芬.关于高职数学函数连续性的教学过程研究[J].广东教育，2019（2）：81-82.

[2]汪富泉，王艳芬.高等数学[M].长春：吉林大学出版社，2016.

[3]郑桂梅.高等数学[M].长沙：国防科技大学出版社，2008.

[4]同济大学应用数学系.高等数学（上册）[M].第五版.北京：高等教育出版社，2002.

[5]侯风波.高等数学[M].上海：上海大学出版社，2009.

◎编辑陈鲜艳

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。