《基于Apriori算法的高职院校课程与毕业能力关联性分析》-教育论文，职业教育论文-论文范文参考-科学狗论文网

标题

基于Apriori算法的高职院校课程与毕业能力关联性分析

范文

向前

[摘? ? ? ? ? ?要]? 利用OBE（成果导向教育）对专业培养目标和毕业能力进行设计并反向设置课程，是当前高职院校构建课程体系的新方法。但此方法在课程设置的有效性、课程和毕业能力之间关联程度的论证上还缺乏相应的分析检验方法和研究。通过建立“课程—能力”矩阵，采用Apriori算法对高职课程与毕业能力的关联性进行分析计算，从而为高职院校课程设置的有效性和合理性提供检验和改进的依据。

[关? ? 键? ?词]? Apriori算法;OBE;课程;毕业能力;关联性

[中图分类号]? G712? ? ? ? ? ? ? ? ? ?[文献标志码]? A? ? ? ? ? ? ? ? ? ? ? [文章编号]? 2096-0603（2020）26-0028-04

一、导言

2020年以来，我国职业教育进入了高速发展时期，经过“国家级示范院校（2005）”“骨干高职院校（2010）”“职业院校教学工作诊断与改进（2015）”“优质高等职业院校（2015）”等建设项目后，2019年起由教育部主导开始实施“双高计划”。虽然在各个时期的建设项目侧重点不同，但其核心内涵和主要工作均是加强专业内涵建设，提高人才培养质量，提升高职院校办学水平。

经过国内各职业院校和诸多学者多年的探索，以常州工程职业技术学院为代表的部分院校于2015年起在“职业院校教学工作诊断与改进”工作中开始借鉴《悉尼协议》和其应用的三个核心概念：“以学生为中心、成果导向、专业持续改进”开展专业内涵建设的研究和实践。其中，采用OBE（成果导向教育）对专业培养目标和毕业能力进行预设，再通过反向设计对专业开设的课程进行设置，成为高职院校新的构建课程体系的主要设计方法。

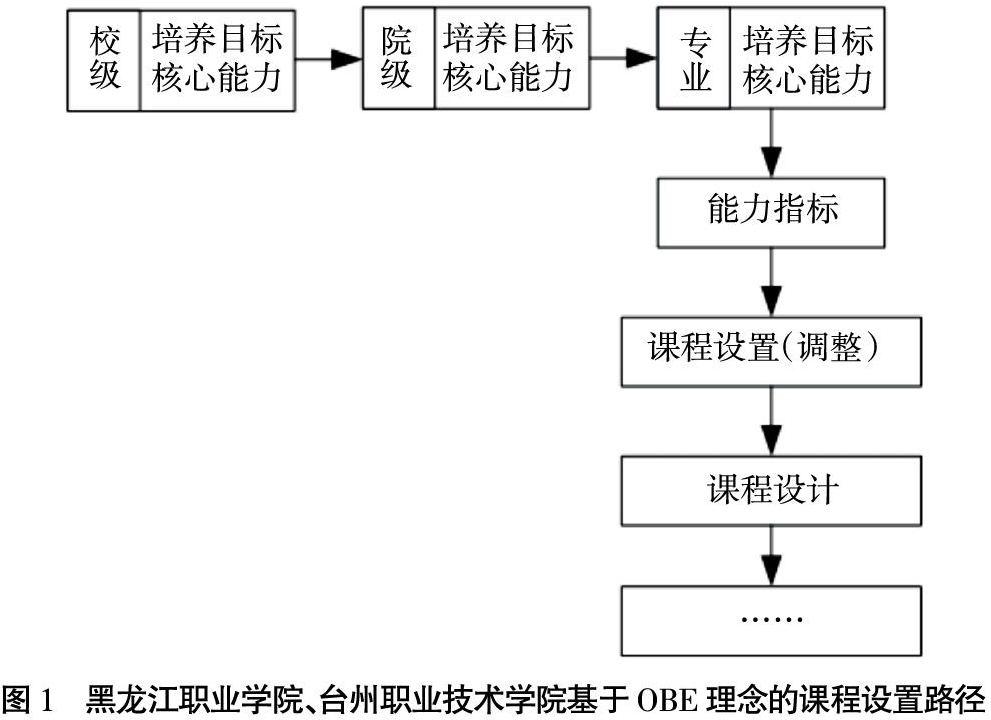
从研究和实践成果上看，黑龙江职业学院、台州职业技术学院等代表性院校在《悉尼协议》本土化研究和实践中，均采用了OBE（成果导向教育）的反向设计方法，按“目标体系构建—课程体系重构”的方式构建课程体系、设置专业课程，其课程设置路径为：

在这一课程设置路径下，“能力指标”与“课程设置（调整）”被关联起来，设计者期望“每一门课程的设置都对核心能力有所支撑，……说明课程开设的必要性，……使课程目标与所属专业能力指标相呼应”（陈丽婷，2018），课程也能更契合培养（学习）目标预期。为使“能力指标”与“课程”的实施和成果可被衡量和评价，两个代表性院校均使用权重赋予的方法开展量化评量。

虽然两个代表性院校均采用权重设置来进行核心能力（毕业能力）占比和课程占比的量化计算，期望能够以此说明课程对核心能力（毕业能力）的支撑度，但是，笔者认为在没有对课程设置进行有效性论证的前提下设置课程权重的量化评量方式，存在主观化、经验主义的缺陷。从学校层面设置权重标准是否符合该校每一个专业的特性？专业的权重比例分配是否科学有效？笔者认为，该量化评量方式没有有效解答这两个疑问，也没有回答并论证毕业生能力目标和课程设置的两个最基本的问题。

（1）课程的设置是否有效？学习目标、培养目标和毕业能力的达成主要是由课程来实现，课程设置的有效性是上述目标达成的前提。只有先证明课程的有效性，才能证明课程的设计和教学是有效的。

（2）课程和毕业能力之间的关联程度如何？一门课程不可能涵盖所有的毕业能力，每一门课程在人才培养过程中所起到的作用更不可能是等效的，那么如何计算并科学表达课程和毕业能力之间的关联关系？

为此，本文通过建立“课程—能力”矩阵，采用关联规则挖掘Apriori算法对高职课程与毕业能力的关联性分析建立模型，期望能为高职院校提供一个有效的课程设置计量分析方法和课程设置改进依据，分析模型为：

二、关联性分析模型构建

（一）构建“课程—能力”矩阵

根据专业培养目标对毕业能力要求、毕业能力要求指标点进行设计，并进行编码转换。

在编码表中，毕业能力要求编码为Bi（i=1，2，…N），表示专业培养目标所设置的所有毕业要求。毕业要求所设置的具体指标点，编码为Bij（i=1，2，…N;j=1，2，…N）。

再对依据毕业能力指标所设置的课程进行编码，编码规则为（i=1，2，…N）。

（二）初始化“课程—能力”矩阵

建立初始化的“课程—能力”矩阵。

三、算法及算例分析

（一）矩阵的布尔运算

建立初始化的“课程—能力”矩阵后，需要在矩阵中进行赋值评价。不同于其他的评价赋值，本研究认为毕业能力指标大部分是描述性的结论、非量化的弹性指标，使用李克特等测量量表赋值说明“毕业能力指标B”由“课程A”实现的度量很难精确，因此本研究在赋值上采用布尔代数，即，只考虑相关（True=1）或不相关（False=0）。

1.布尔运算赋值条件设定

对毕业能力指标B与课程A完全不相关、相关或完全相关成立的条件进行设定：

条件1：课程Ai的课程目标和主要授课内容能直接培养该毕业能力Bi;例如，沟通技巧课程直接培养毕业能力B11“能准确、简练地使用普通话或使用书面语言进行有效沟通的表达”（以下以B11代替该毕业能力的内容）。

条件2：课程Ai的课程目标和主要授课内容不能直接培养毕业能力Bi，但满足：（1）在课程Ai中毕业能力Bi是成绩评价的重要组成部分;（2）通过课程Ai的教学环节能有效提高毕业能力Bi;（3）成绩评价和能力提高是可被记录和衡量的。例如，思想道德修养课程（以下简称“思修”）不直接培养毕业能力B11，毕业能力B11也不是思修课程成绩评价的重要组成部分且不需要衡量，则视为不满足条件2。课程“酒店前厅”不直接培养毕业能力B11，但在课程主要教学和实训环节中需要学生进行有效溝通，且沟通是否得当是课程“酒店前厅”成绩评价的重要组成部分，则视为满足条件2。

布尔运算的条件假设需要使专业所设置的课程能与毕业能力最大程度的关联，笔者认为只有这样才能打破课程与课程间的壁垒，使课程相互关联、相互支持。

2.布尔运算赋值

True：毕业能力指标B与课程A可以相关或完全相关，满足条件1，或不满足条件1但满足条件2，赋值为1。

False：毕业能力指标B与课程A完全不相关，不满足条件1或2，赋值为0。

3.布尔运算

根据布尔运算的赋值假设条件，可组织企业、专业人士对“课程—能力”矩阵进行赋值评价。表5为企业对“毕业能力指标点Bij”是否与“课程Ai”的赋值表示例，1表示相关，空格（0）代表不相关。

（二）Apriori算法下的高职“课程—能力”关联度

1.Apriori算法分析

Apriori算法是挖掘布尔运算关联规则频繁项集的算法，包含支持度计算和置信度计算，本算法采用的公式为：

设课程合集A，毕业能力指标合集B为关联性数据，对应的支持度为：

设课程合集A对毕业能力指标合集B的置信度为：

利用公式（1）、（2）对布尔运算赋值后的“课程—能力”矩阵进行计算。为了提高运算效率，减少候选集多、运算时间长等问题，常规或改进的Apriori算法会将频繁性小的数据删除，但对于课程和毕业能力关联性挖掘而言，只要两者之间有关联性就需要最大限度地探讨课程支持毕业能力达成的可能性。为此，笔者在实际计算过程中未去除频繁性小的数据，而是得到所有关联结果后再进行调整。

在笔者构建的酒店管理专业“课程—能力”矩阵实际算例中，课程合集为Ai（包含通识课程），毕业能力合集为Bi，Bi={B1=（B11，B12，B13，B1j），…Bi=（Bi1，Bi2，Bi3，Bij）}，i=1，2，…N;j=1，2，…N。計算时，只计算毕业能力指标合集Bi的值。最终分析结果为：

Apriori算法分析结果1：为使所有课程都能与毕业能力相关联，即，所有课程与毕业能力至少相关1次，设最小置信度阈值=0，共有关联结果198个。

Apriori算法分析结果2：为使所有毕业能力都能与课程相关联，即，所有毕业能力与课程至少相关1次，设最小置信度阈值=0.007，共有关联结果56个。

在表6的算例分析示例中，rules为关联规则，support为支持度，confidence为置信度，lift为关联次数。关联度计算结果反映的是毕业能力要求究竟与哪些课程相关且关联程度如何，如，rules143代表毕业能力要求B2与课程A19相关联，但弱于rules195毕业能力要求B8与课程A14的关联度。

2.关联性区间的划分

为更好地利用Apriori算法结果进行分析，可以对毕业能力要求与课程之间关联性强弱划分区间。“Apriori算法分析结果2”虽然保证了每一个毕业能力指标都与课程相关，但从算例结果来看有12门课程不在关联结果中，其中10门为通识课程，2门为专业课程。为更全面地对课程和毕业能力关联性强弱进行分析，笔者在关联性强弱区间划分上采用的是“Apriori算法分析结果1”的数据。

（1）关联性强弱区间设定

强区间Ⅰ：Support=0.01308900523560210，rules=198-195;

强区间Ⅱ：Support=0.01047120418848170，rules=194-170;

强区间Ⅲ：Support=0.00785340314136126，rules=169-143;

弱区间Ⅰ：Support=0.00523560209424084，rules=142-107;

弱区间Ⅱ：Support=0.00261780104712042，rules=106-1。

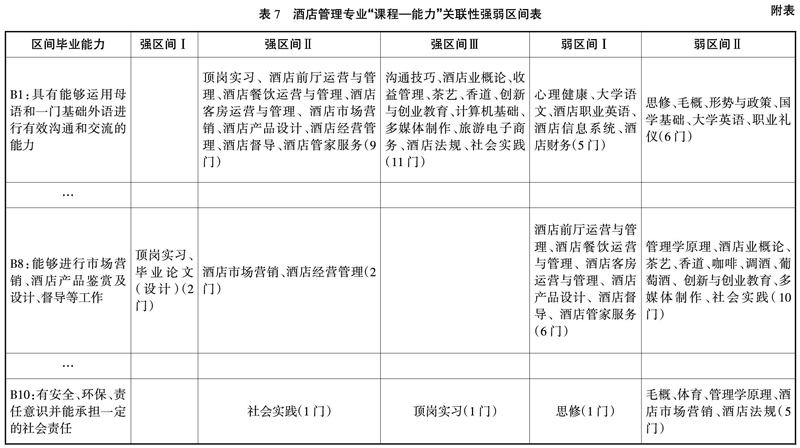
（2）“课程—能力”关联性强弱区间表（见附表）

按“Apriori算法分析结果1”对课程进行汇总。

（三）毕业能力与课程关联性分析结果

根据表7算例结果，处于毕业能力关联性强区间中的课程，应分别向相应的毕业能力倾斜，使课程目标的侧重点更为明晰。如，有9门课程处于毕业能力“B1：具有能够运用母语和一门基础外语进行有效沟通和交流的能力”的强区间Ⅱ中，且均为专业课程，表明上述课程在课程设计和教学中应重视沟通能力的培养。对于毕业能力“B8：能够进行市场营销、酒店产品鉴赏及设计、督导等工作”，顶岗实习、毕业论文（设计）2门课程处于强区间Ⅰ中，这为专业实践教学改革提供了新的思路，有助于专业厘清学生培养方向和培养特色。

处于毕业能力关联性弱区间中的课程，一方面对是否应该开设该课程再加以分析和甄别，另一方面则需要从课程改革着手，增强课程在教学育人中的作用。受篇幅影响，本文不展开论述。

四、结论

利用Apriori算法对高职课程与毕业能力的关联性分析，其实质是计算某专业设置的课程对毕业能力达成的支持度。相对于直接赋予课程权重来支持毕业能力达成等其他方法，本方法一方面可以预先检验课程设置是否有效地支撑了预设的毕业能力目标，另一方面又能量化课程对毕业能力支持的程度。

但在Apriori算法分析结果中需要注意的是，笔者的算法分析是对专业所设置的所有课程进行计算，其中出现了绝大多数通识课程和少量的专业课程处于与毕业能力关联度的弱区间。对于关联性处于弱区间Ⅰ、Ⅱ的专业课程，可以分析并研究是否合并或删减，调整课程设置;但是，通识课程因其特殊性，则不能简单地删减处理，而需要重新思考如何加强通识课程的课程建设与改革，提高通识课程对毕业能力的支持度。笔者下一步也将在Apriori算法的基础上，结合其他算法进一步研究。

参考文献：

[1]王晓辉，周雪芳，刘国新.关联规则Apriori算法的研究和改进[J].信息与电脑（理论版），2019（5）：71-72.

[2]葛璐瑶.关联规则挖掘Apriori算法应用研究[J].计算机产品与流通，2018（8）：185.

[3]陈丽婷.《悉尼协议》范式下高职专业建设的本土化实践[J].中国职业技术教育，2018（22）：59-65.

[4]王成勇.关联规则Apriori算法的研究与应用[D].北京：华北电力大学，2018.

[5]李潇.基于数据挖掘Apriori算法实现与应用[J].电子世界，2017（1）：148，150.

[6]吐尔逊·买买提，乌木提·热夏提.基于Apriori的课程关联模型研究[J].农业网络信息，2016（12）：136-139.

[7]牛猛.Apriori算法的研究与实现[J].赤峰学院学报（自然科学版），2016，32（8）：24-26.

编辑陈鲜艳

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。