《艾宾浩斯遗忘曲线在中职数学概念教学中的应用》-教育论文，职业教育论文-论文范文参考-科学狗论文网

标题

艾宾浩斯遗忘曲线在中职数学概念教学中的应用

范文

焦大伟+黄苏燕

摘要：中职学生的学习兴趣不高，对数学概念的理解和掌握相对浅显，遗忘较快。本文重点研究如何利用艾宾浩斯记忆保持或遗忘规律提升和增强学生数学概念的记忆能力，进而提高中职学生的数学学习能力。

关键词：中职数学概念艾宾浩斯

一、数学概念在中职数学中的重要性

中职数学是中等职业学校学生必修的一门文化基础课，中职数学课程的任务是使学生掌握必要的数学基础知识，具备必需的相关技能与能力，为学习专业知识、掌握职业技能、继续学习和终身发展奠定基础。而数学概念的学习是中职学生学习中职数学知识、训练基本技能、进行逻辑推理的基础，在中职数学教学中起着非常重要的作用。如果学生基础的数学概念掌握不好，学习其他数学知识就如无源之水、无本之木。

二、艾宾浩斯记忆和遗忘的规律

我们知道遗忘是记忆的对立面，凡是被遗忘的事物就是不能记忆的事物，凡是能记忆的事物就是没有被遗忘的事物。因此，从某个角度上讲，遗忘是中职数学教学的天敌，在中职数学教学中，教师要善于运用科学的方法，帮助学生更好地保持记忆，减少遗忘。笔者借鉴德国心理学家赫尔曼·艾宾浩斯的遗忘规律来探索中职数学概念的教学。

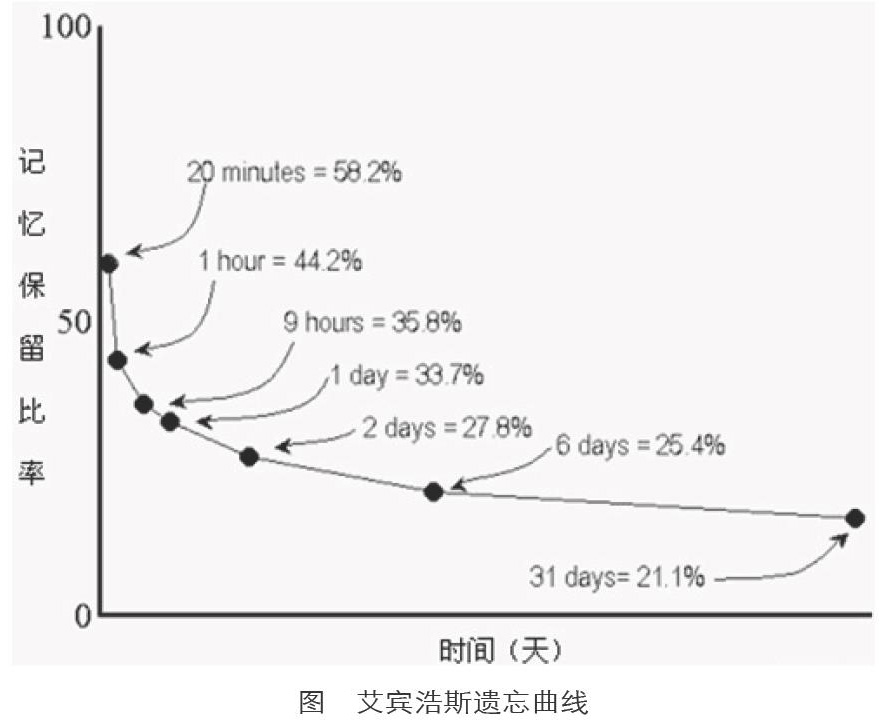
艾宾浩斯依据实验的数据绘制出遗忘曲线，人们称之为艾宾浩斯遗忘曲线，见图。

艾宾浩斯遗忘曲线解释了遗忘在数量上受时间因素的制约规律：遗忘量随时间递增，遗忘的速度是先快后慢，在识记后的短时间内遗忘特别迅速，然后逐渐缓慢，也就是说遗忘的进程是先快后慢。

三、艾宾浩斯记忆和遗忘规律在中职数学概念教学中的实际应用

根据艾宾浩斯记忆和遗忘规律，结合中职学生学习数学的特点，笔者总结出了中职数学概念“简单化、复现化”相结合的教学复习方法。

1.數学概念“简单化”教学方法

艾宾浩斯分别在早期、晚期进行了“音节组的长度和学习速度的关系”试验，通过有效的数据分析，他发现：识记一组概念，概念组越大，识记就越困难。同时，艾宾浩斯通过数据分析还发现了“学习有意义的材料时学习速度的增加”。因此我们在进行数学概念的教学时，应尽可能的简化概念，并改进教学方法或手段，优化数学概念的讲授方法，加快学生的学习和记忆速度。

（1）从数学概念的字面意思上入手。中国的汉字文化博大精深，专家们都是用了最简洁的词语概括出了数学概念，既然简洁，我们又何苦将其复杂化。例如“集合”这个概念，学生们从幼儿园开始在做操等活动中就在体会“集合”的含义，因此在授课时笔者会直接告诉学生：“集合，与大家从小到大体会到的意思一样，就是按照要求把该放在一起的人或东西放在一起。例如体育老师喊集合时，同学们会站到自己班级的队伍里，而不是其他班的。我们这个班级就是一个集合。”听了这样的解释，学生们能比较轻松地理解了“集合”这个数学概念。

又例如，在讲授“数列”的概念时，笔者将其概括为“数列就是一列数”；在讲授“等差数列”的概念时概括为“等差数列就是差相等的一列数”；在讲授“等比数列”的概念时概括为“等比数列就是比（值）相等的一列数”；还有“向量就是有方向的量”。

对数学概念进行如此简洁的概括，主要的目的是促使学生能很快地了解这些数学概念所蕴含的意思，建立自信心，这样的安排使得学生们更容易记住所学数学概念，并愿意对其进行深入理解。

（2）从数学概念的相互关联上入手。学生对不熟悉材料的遗忘速度快于熟悉材料的遗忘。因此在数学概念的教学中，我们也要关注数学概念间的联系，通过联系记忆、比较记忆等方法，将新的数学概念与学生的原有知识联系起来，促进学生数学概念的学习。例如，讲授“余弦函数的图象和性质”之前，学生们已经学习了“正弦函数”的相关知识，因此我们只要通过“”诱导公式将正弦函数和余弦函数建立起联系，学生就能比较轻松地学习“余弦函数的图象和性质”。再例如，由于“圆的定义（圆是平面内到定点的距离为定长的点的轨迹）”“椭圆的定义（椭圆是平面内与两个定点的距离之和为常数的点的轨迹）”“双曲线的定义（双曲线是平面内到两个定点的距离之差的绝对值为常数的点的轨迹）”都是有关点的轨迹方程，因此在讲授“椭圆的定义”“双曲线的定义”时，我们引导学生和“圆的定义”比较着进行学习，促进了学生的理解和记忆。

（3）从数学概念的实际应用上入手。学生对无意义的学习材料的遗忘速度快于对有意义的学习材料的遗忘。在数学概念的学习过程中，学生经历数学概念的形成与应用之后，能更好地理解抽象的数学概念的意义，发展应用数学概念。

例如，“函数的概念”对于中职学生来说一直都是无法言语的痛。“函数的概念”定义的非常抽象，学生难以从定义的字里行间理解其含义，因此笔者在教学时列举了大量的实例：售卖商品的数量和收入之间的关系，日气温与时间之间的关系，还有心电图等等。笔者通过引导学生寻找体验实际案例中存在的变量关系，简化函数的概念，帮助学生理解“函数其实就是两个变量之间的依存关系”。

再有，立体几何相关概念的讲授一直是中职数学教学的一大难点，因为它相对其他知识点来说更加抽象，需要学生有较强的空间想象能力，但这恰恰又是学生所缺乏的。那如何让学生有立体感，从而学好立体几何的相关概念呢？笔者是这样操作的：课堂上充分利用起学生最常用的“笔”和“书”，将其作为直线和平面的模型，模拟各种线面、面面关系；或者列举定理的一些实际应用，引导学生理解定理的形成过程。

2.数学概念“复现化”保持方法

艾宾浩斯在研究记忆的保持时，发现记忆的保持与诵读次数、回忆复习以及识记的顺序都有一定的关联。对于学生学过的数学概念，它们不会自动浮现到学生的意识中去，而是需要我们数学教师引导学生在途中把它们迎接回来。当学生将数学概念复习到一定程度时，它们就能准确无误地再现出来。

（1）间隔诵读。艾宾浩斯在研究记忆保持和诵读次数的关系时指出：诵读的次数逐步增加，音节组就被镂刻得越来越深，越不易冲刷掉；如果诵读的次数少，镂刻仅是在表面，只能暂时看出大致的轮廓；如果诵读的次数更多，24小时以后几乎可以自动地背诵出来，再增加诵读次数的效果就很小了。根据上述研究，在数学概念的教学之后，笔者都会留出时间让学生诵读3遍概念；在例题或练习题运用概念前，还是让学生先诵读概念再解题；在课堂小结过程中，仍然让学生诵读概念。诵读数学概念也成为了学生们的课后作业，笔者会通过检查录音的形式进行抽查。通过利用重复诵读的最佳24小时，学生对数学概念的记忆效果普遍增强。

（2）回忆再现。多次反复诵读的效果的规律性并没有明显地离开艾宾浩斯遗忘曲线的研究结论，因此为了促进学生对数学概念的保持，除了要利用好24小时的诵读影响外，还要在之后的若干天让学生保持诵读。但同时我们需要注意的是：伴随回忆的诵读要比没有伴随回忆的诵读所需的次数少、效果好。在数学教学中，我们要善于引导学生回忆再现数学概念。例如在课后小结中，通过师问生答，让学生回忆再现当堂所学概念；在课堂开始时，也通过提问等形式，引导学生对已学过的数学概念进行回忆。每节课如此，引导学生慢慢养成良好的学习习惯。

（3）复习巩固。结合艾宾浩斯遗忘曲线前阶段遗忘速度较快的特点，在数学概念学习后的20分钟需要及时的巩固提高。在实际课堂操作中，笔者在数学概念的教学后，会辅助以典型的例题分析、讲解，加深学生对概念的理解和认识。在例题分析结束后，对学生进行配套的课堂练习或者课堂测试的形式加以复习和巩固。同时，除了每天根据数学概念安排的课后作业外，每一周笔者都会增加一份综合练习卷，题目不多，但涉及到的知识点逐步增加，这样在某种程度上就提高了学生对数学概念的记忆。

四、艾宾浩斯记忆和遗忘规律在中职数学概念教学应用中的思考

数学概念的记忆是数学学习中的重要环节，也是提高学生数学能力的有效途径。艾宾浩斯的研究成果可以成为我们研究中职数学概念教学的实践依据，而且在进行数学概念的教学实践时，我们会发现按照艾宾浩斯的研究结果去组织实施概念教学及巩固，也确实获得了良好的效果。但是由于学生存在个体差异，他们的记忆和遗忘的时间也都各不相同，因此教师还应该根据艾宾浩斯记忆和遗忘规律制定符合学生个性化的数学概念学习、记忆方法。

参考文献：

[1][德]赫尔曼·艾宾浩斯（Ebbinghaus，H.）著，曹日昌译.记忆[M].北京：北京大学出版社，2014.

[2][德]赫尔曼·艾宾浩斯（Ebbinghaus，H.）著，王迪菲编译.记忆的奥秘[M].北京：北京理工大学出版社， 2013.

[3]田金枝.论记忆与数学学习[J].职教论坛， 2010（1）.

[4]王慧颖.数学概念记忆两法[J].黑龙江教育小学教学案例与研究，2009（4）.

（作者单位：绍兴市技工学校）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。