张文涛
【摘要】“数”和“形”是数学中最常见的两种元素,也是数学学科最基础的研究对象,因此,利用数形结合思想来解答数学问题是常用的方法,也是学生应当具备的解题能力之一.因此,在高中数学教学中,教师应当结合数形结合思想,将抽象的数学语言转换为直观的图像,使数学问题变得简单、易懂.本文就结合具体的例子探讨数形结合思想在高中数学教学中的运用,以期帮助学生高效理解和掌握所学知识,同时提高学生的解题能力.
【关键词】高中数学;数形结合思想;运用
数形结合思想是数学学习中一种常见和常用的数学思想.所谓数形结合,就是将抽象的数学语言与直观的图像结合起来,把复杂的数量关系转化为可视的图形,使数学问题直观化、具体化.运用这种数学思想,能使学生发散数学思维、理清解题思路、找准解题方向、快速解答问题.在高中数学教材中,有很多知识体现了数形结合思想,因此,在教學中,教师应结合具体的教学内容,合理应用数形结合思想,帮助学生理解和掌握所学知识,同时促进他们数学解题能力的提高.笔者根据自己的教学实践和经验,对数形结合思想在高中数学教学中的应用进行了探讨,不足之处还望广大同仁指正.
一、利用数形结合思想解决集合问题
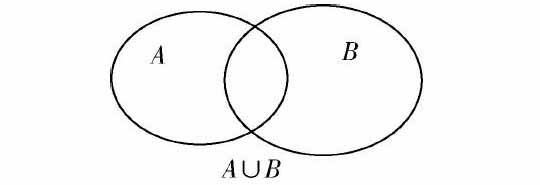
集合是高中阶段非常重要和基础的内容,安排在高一上册第一章,也就是说,学生进入高中阶段后,首先学习的内容就是集合.因此,集合是高中阶段的数学课程的第一个概念,也是学生学习其他数学概念、数学定理的基础.但是,对高一新生来说,集合的知识是比较抽象的,他们理解起来有一定的难度,尤其是交集、并集、补集的关系和运算是本章的重点,也是主要的考查内容.为了帮助学生真正理解和掌握集合的相关内容,教师可以运用数形结合思想,把抽象的交集、并集、补集等数量关系,用直观的图形展示出来.集合的数形关系通常利用Venn图(如图,两个图形的所有部分就是集合A与集合B的并集)和数轴展示,具体来说,Venn图常用来解决较为具体的集合问题,即集合中的各个元素已经明确,通过作Venn图,学生可以快速直观地得出答案;数轴常用来解决和处理用不等式表示的集合问题,即根据题意作数轴,在数轴上标出各个集合的关系,这样就能将各个集合的运算转化为相对应的不等式之间的运算.
二、利用数形结合思想解决函数问题
函数是中学数学的重要学习内容,不管是在初中数学中,还是在高中数学中,都占有很大的比重,而且是教学的重点和难点.同样的,这部分知识也是学生的学习难点,尤其是函数中各个变量之间的关系有较强的抽象性,学生理解起来有很大的难度.在高中阶段,学生需要学习和掌握的函数包括指数函数、对数函数、幂函数、反函数等,不同的函数,其性质也各不相同.如果仅凭教师的讲解,学生很难掌握这些函数的数量变化关系,为了帮助学生理解和掌握函数知识,教师可以将数形结合思想应用到函数教学中,将抽象的函数知识转化为直观形象的图形,使学生借助图形来理解函数中的数量关系,进而处理和解决相关数学问题.例如,在让学生解答“已知函数f(x)=sinx+2sinx,x∈[0,2π]的图像与直线y=k有且仅有两个不同的交点,求k的取值范围”这一函数类问题时,教师就可以引导学生根据题目中的两个函数解析式来作图,先画出坐标系,然后根据题目中的已知条件画出两个解析式对应的图像,再依据图像来分析题目中的数量关系,这样,抽象的数量关系就变得具体、直观,学生就能在作图的过程中理解题目含义、掌握数量关系,进而快速准确地解答问题.
三、利用数形结合思想解决平面解析几何问题
平面解析几何是高中数学的学习重点和难点之一,其本质是利用代数的方法研究平面图形的几何性质.这部分数学知识有较强的抽象性,如果只是让学生从数的角度来思考、分析、解答问题,势必会给学生造成较大的困扰,因此,教师在讲授平面解析几何内容时,应当将数形结合的思想贯穿教学始终,通过数形之间的相互转化,降低学生的学习和理解难度,使他们既能够学会用方程来表示直线、曲线以及二者的位置关系,还能够结合直线、曲线的性质来求出相应的方程.概括来说,就是让学生学会几何问题和代数问题的相互转化.例如,有这样一道解析几何题:假设曲线x2+y2=2(y≥0)与直线y=x+b有两个交点、一个交点、无交点这三种情况,请分别求出每种情况下b的取值范围.如果学生利用代数的方法来解答问题,就对学生的逻辑思维提出了很高的要求,而且解答问题的过程比较复杂,而利用数形结合方法,让学生在坐标系内先画出曲线,然后根据曲线和直线的交点数量的不同,在坐标系内移动直线,就能把抽象、复杂的问题变得具体、简单,学生很快就能解答出来.
实际上,数形结合思想在高中数学中的应用不仅仅体现在以上几方面,还在数列、立体几何、线性规划、方程与不等式等多个问题中也贯穿着这一数学思想.限于篇幅有限,笔者只从上述三方面探讨了数学结合思想的运用,希望学生能够真正掌握这一思想,将抽象的问题转化为简单易懂的问题,进而理清解题思路、简化解题过程、提高解题能力.
【参考文献】
[1]王英.数形结合思想在高中数学教学中的应用[J].高考,2015(1):135.
[2]张艳.数形结合思想在高中数学教学中的应用研究[J].中国校外教育,2016(11):55,57.
[3]陈荣辉.渗透数形结合思想,提高高中数学教学效果[J].数学学习与研究,2015(9):58.
- 英汉形容词差异及对外汉语教学策略
- 小学语文教学中的文学素质培养
- 谈思维导图在初中语文教学中的有效运用
- 让传统古诗词文化在终身学习中留香
- 发挥语文阅读综合教学作用,提升小学生语文素养
- 从班级共读《木偶奇遇记》入手,浅谈朗读在课外阅读中的意义
- 浅谈课外阅读在小学语文作文教学中的重要性
- 关于提升小学语文教学质量的探讨
- 探究小学语文易错生字原因与对策
- 立足语用 个性飞扬
- 浅谈小学语文教育中的情感教育实施策略
- 当前城市独生子女心理健康方面存在的问题及教育疏导策略
- 基于人才成长的后进生转化策略
- 智能手机对小学生心理危害的现状分析及对策
- 浅谈在初中古诗词教学中强化传统文化教育的策略
- 微课在高中语文古诗词教学中的应用价值初探
- 家校共育单亲家庭孩子的策略与方法
- 农村小学培育和践行社会主义核心价值观的长效机制探究
- 以星光班级证书为载体促进学生综合素质
- 高中语文生活化教学方法微探
- 利用翻转课堂培育语文核心素养
- 高中语文教学中运用“互联网+”培养学生研究性学习能力的探究
- 利用绘本开展小学生生命教育课程的探讨
- 基于BYOD进行项目式学习 培养学生良好的语文核心素养
- 着实抓好低年级学生写日记习惯的培养
- hackable
- hack-around
- hack-down
- hacked
- hacked off
- hacker
- hackerdom
- hackers
- hackest
- hacking
- hack into
- hack into sth
- hack-it
- hackneydom
- hackneyed
- hack's
- hacks
- hacksaw
- hacksawed
- hacksawing
- hacksaws
- hackster
- hack-up
- hack²
- hack¹
- 一宗未了又一宗
- 一宗款项
- 一官半职
- 一定
- 一定不易
- 一定不移
- 一定不能缺少
- 一定中
- 一定中、两相好、三桃园、四季财、五魁首、六六顺、七巧巧、八匹马、久久长、全来到
- 一定之法
- 一定之规
- 一定之计
- 一定之论
- 一定会有报应
- 一定区域一定时间内的各种气象变化情况
- 一定历史时期诗歌创作的倾向
- 一定地区较长时间总体的气象情况
- 一定地域内的自然物及自然现象形成的可供人观赏的景象
- 一定地点上面的天空
- 一定场合下的情景
- 一定场合的情况、光景
- 一定失败的局面
- 一定季节的天空
- 一定时间内停止通航
- 一定时间内能发生的效用