《《相似三角形的基本型》教学设计》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

《相似三角形的基本型》教学设计

范文

贾国红

一、教学内容分析

《相似三角形》是人教版义务教育课程标准实验教科书《数学》（五四学制）第二十七章的内容，是全等变换之后的又一种图形变换.全等是相似的一种特殊情况，从这个意义上讲，相似比全等更具一般性.本节课主要复习了相似基本型，通过对相似基本型的归纳总结和习题的变换训练，加深了学生对变换思想的认识，熟练了相似基本型的综合运用.

二、教学对象分析

九年级学生已经学习了相似三角形的性质和判定，并进行了简单的练习，但是在解决稍复杂的问题时，不会灵活运用相似基本型解决问题.针对此情况，我设计了这节复习课，加强学生对相似基本型的理解和应用.

三、教学目标及教学重难点

1. 教学目标

知识与技能：理解相似基本型的区别和联系，能灵活运用相似基本型解决相关问题.

过程与方法：经历观察、思考、小组探究等活动，进一步体会转化的思想.

情感、态度与价值观：通过学生观察、思考、小组探究等活动，提高学生合作交流能力、主动参与意识.通过小组合作交流活动，提高学生语言表达能力和逻辑思维能力.

2. 教学重点：相似三角形的基本型.

3. 教学难点：相似基本型的综合应用.

四、教学方法、过程及整合点

1. 教学方法

依据学生认知规律，遵循“学生为主体，教师为主导，数学活动为主线”的指导思想，采用以启发引导为主，直观演示法为辅的教学方法.适时运用多媒体教学，充分发挥现代教学手段的优越性.

2.学习方法

根据学法指导自主性和差异性原则，让学生在“思考—操作—交流—归纳”的实践探索中自主参与知识的产生、发展、形成与应用的过程，引导学生自己发现问题、提出问题、解决问题、拓展问题，指导学生用观察、抽象、自主探究为主、合作交流为辅的方法进行学习.

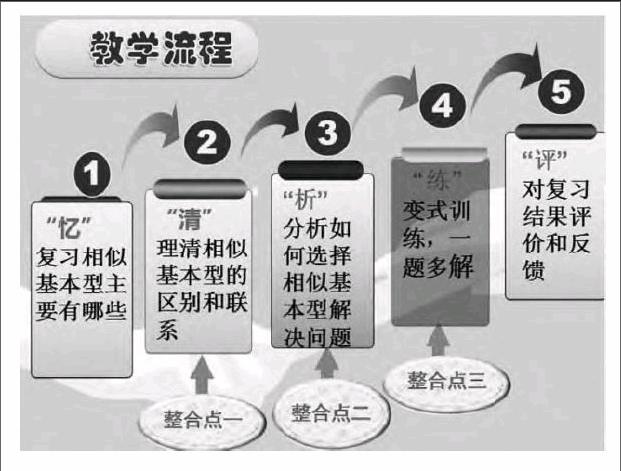
3.教学过程及整合点

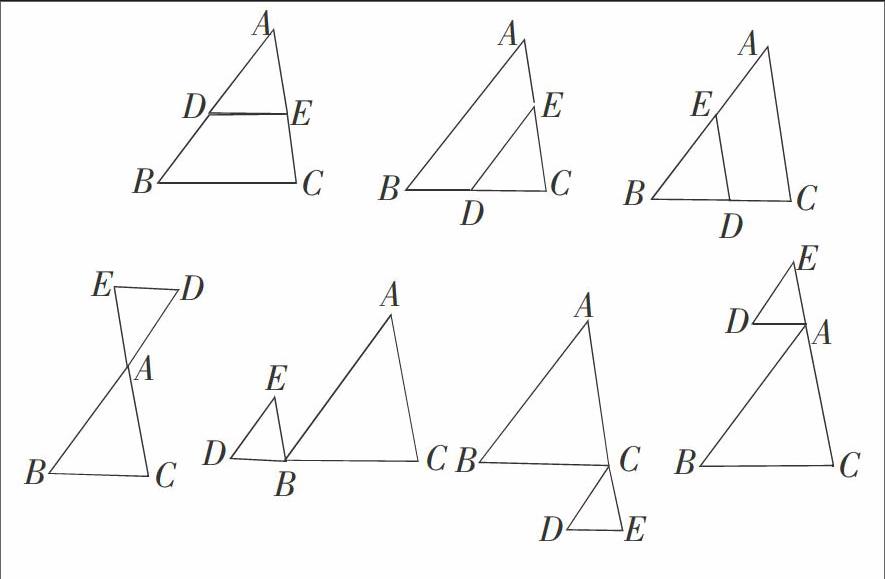
（1）“忆”——复习相似基本型主要有哪些

师生活动：总结相似基本型主要有三种：A型、X型、M型.

（设计意图：回忆相似基本型的三种类型，加深对知识的整体认识.）

整合点与软件：几何画板演示三种图形，形象直观.

（2）“清”——理清相似基本型的区别和联系

师生活动1：观察A型、X型、M型这三种相似基本型的区别，再思考它们之间有什么联系.

师生活动2：小组交流三种相似基本型的区别和联系.

师生活动3：归纳相似基本型的区别和联系，突出本节课重点.

（设计意图：经历教师的演示、学生的探究过程，体会相似基本型之间的联系和区别，为解决综合题埋下伏笔.）

整合点与软件：此环节是信息技术与课程整合点之一.几何画板的充分使用，解决了传统教学中教师难以讲述，学生难以理解的内容.

（3）“析”——分析如何选择相似基本型解决问题

师生活动1：相似基本型的应用

如下图，等边△ABC中，D为BC中点，∠EDF=60°，当∠EDF旋转一个角度时，观察探索△BED和△CDF有什么关系.

师生活动2：找出△BED和△CDF相似，是M型相似.

师生活动3：如下图，将等边三角形变为等腰三角形，将中点D变为一般点D，结论还成立吗？

师生活动4：总结解决问题的关键是找出相似基本型，为解决相似基本型的综合应用这一难点打下基础.

（设计意图：此题是探索题，通过对等边三角形中相似基本型M型的探索，发散学生的思维，锻炼学生的毅力，同时也体现了团队合作精神.总结图形相似的有关特征并自觉应用到变式中，进一步丰富数学活动经验，培养应用数学知识解决问题的能力.）

整合点与软件：此环节是信息技术与课程整合点之二，这是一个动态图形，从中找出静态图形，利用几何画板将相似三角形拖拽出来，使学生看得更清晰.

（4）“练”——变式训练，一题多解

师生活动1：提出动点问题.

已知菱形ABCD，AB=4cm，∠B=60°，点P、Q分别从点B、C同时出发，沿线段BC，CD以1cm/s的速度向终点C，D运动，运动时间为t秒.连AP，AQ，PQ，试判断△APQ的形状，并说明理由.

学生观看演示，独立思考，体会动点问题中哪些图形全等，老师总结动中的不变.

师生活动2：如何解决动点问题和相似基本型的综合题.

连接AC，与PQ相交于K，当t=1秒时，求AK的长.

学生探究后派代表演示找出的相似基本型.

师生活动3：由于学生表述得不够完整，教师将找到的基本型进行演示，突破本节课难点.

（设计意图：此题是探索结论题，体现了层次性，呈阶梯逐步加深、加难，通过对结论的探索，复习相似三角形中的基本型.通过一题多变，培养学生的发散思维，拓展学生的解题思路.）

整合点与软件：此环节是信息技术与课程整合点之三.几何画板的充分使用，变抽象为形象，变复杂为简单，动中有静，静中有动，形象具体.几何画板呈现相似基本型，并从复杂的图形中抽象出来，寻找题中的变量和不变量.

（5）“评”——对复习结果评价和反馈

师生活动：用“问卷星”的形式小结反馈.

（设计意图：用此形式，可以灵活掌握学生对所学内容的掌握情况，以便对个性问题个别辅导，对共性问题集中讲评.）

五、教学环境

根据教学内容、学生情况以及学校的实际情况，利用几何画板可以图文并茂、声像并举、形象直观地为学生创设各种情境，激起学生的各种感官参与，激发学生学习动机和兴趣.数学科学的特点是逻辑性强、抽象思维要求高，尤其是空间问题、动态过程问题等学生不易理解的问题，通过这种方式可以使复杂的问题转化为直观、形象、生动的感性情景，大大降低了学生的理解难度和教师的教学难度.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。